5. 2 Астатическое регулирование

Часто требуется полное устранение статизма системы. Для того, чтобы выяснить пути полного устранения статизма, обратимся вновь к общему выражению для y_ст, полученному через передаточную функцию путем подстановки в нееp=0:

, (5.15)

При наличии f_стстатическое отклонение будет отсутствовать, если приp=0выражениеW_з(p)обратится в нуль. Это возможно в двух случаях: еслиW_fy(0)=0или еслиW(p)=. Первый путь реализуется введением компенсирующего воздействия по возмущению и рассматривался нами ранее при анализе систем с принципом управления по возмущению (1.211.23). Второй путь реализуется введением в систему интегрирующего звена, т.е. переходом к так называемой астатической системе управления. Такую систему можно получить, если ввести в рассматриваемую статическую САУ интегрирующее звено так, чтобы оно находилось вне участка системы от места приложенияfдоy, т.е. чтобы его передаточная функция не входила вW_fy(p). В этом случае, как следует из (5.15), статическое отклонениеy_стбудет равно нулю, так как при конечном значенииW_fy(0)=K_fyимеемW_p(0)=из-за наличия в знаменателеW_p(p)множителяp, обязанного своим появлением передаточной функцииинтегрирующего звена.

Наличие интегрирующего звена между точками нахождения fиy, т.е. в составе передаточной функцииW_fy(p), не устраняетy_ст. Это легко показать, используя выражение (5.15).

Таким образом, для получения астатической САУ достаточно в замкнутый контур регулирования ввести интегрирующее звено. В связи с этим, интегрирующее звено часто называют астатическим. Астатическим называется элемент, у которого при постоянном входном воздействии сигнал на выходе в установившемся режиме непрерывно растет с постоянной скоростью, ускорением и так далее.

Вернемся к нашему примеру. Если вместо усилительного звена поставить ПИ-регулятор с передаточной функцией

, (5.16)

то статизм системы станет равным нулю. Структурная схема такой системы представлена на рисунке 5.4.

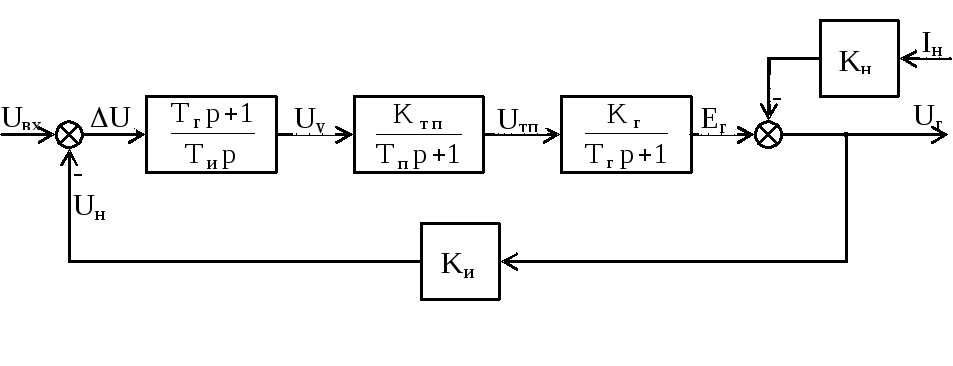
Рисунок 5.4 Структурная схема астатической системы автоматического регулирования напряжения генератора

Передаточная функция замкнутого контура относительного возмущающего воздействия в виде

, (5.17)

откуда следует, что по окончании переходного процесса отклонение выходной величины U_гравно 0, т.е. система астатическая относительно возмущающего воздействия.

Записывая передаточную функцию относительно входной величины U_вх, получим

, (5.18)

Из выражения (5.18) следует, что система статическая относительно управляющего воздействия.

Таким образом, одна и та же САР может быть статической по отношению к какому-либо возмущающему воздействию и астатической по отношению к управляющему воздействию, и наоборот.

Глава 6. Устойчивость систем автоматического управления

6. 1 Понятие об устойчивости

Понятие устойчивости системы управления связано со способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Устойчивость - это свойство системы возвращаться в исходное или близкое к нему установившееся состояние после всякого выхода из него в результате какого-либо воздействия.

Из данного определения следует, что устойчивость связана с характером переходных процессов и состоянием системы после окончания переходного процесса, т.е. является основной динамической характеристикой системы. Поэтому анализ устойчивости САУ является основной проблемой в теории автоматического управления.

В зависимости от характера переходного процесса различают три основных случая поведения системы после приложения возмущающего воздействия:

1. система не может восстановить равновесного состояния, значение управляемой переменной все больше отклоняется от заданного (рисунок 6.1, а); такой процесс называется расходящимся, а система – неустойчивой;

2. система возвращается к равновесному состоянию, значение управляемой переменной отличается от заданного на величину статической погрешности системы; такой переходной процесс будет сходящимся, а система - устойчивой (рисунок 6.1, б);

3. система характеризуется установившимся периодическим движением; такой процесс называется незатухающим колебательным, а система будет находится на границе асимптотической устойчивости (рисунок 6.1, в).

Рисунок 6.1 Поведение системы после приложения возмущающего воздействия

Рассмотрим, от чего зависит устойчивость системы и чем она определяется. Пусть динамика линейной системы описывается линейным дифференциальным уравнением с постоянными коэффициентами:

, (6.1)

Решение такого линейного неоднородного уравнения в общем случае из двух составляющих:

, (6.2)

где

y_уст(t)- частное решение неоднородного уравнения (6.1) с правой частью, описывающее вынужденный режим системы, устанавливающийся по окончании переходного процесса; такие режимы нами были рассмотрены в предыдущем параграфе;

y_п(t)- общее решение однородного уравнения, которое описывает переходный процесс в системе, вызванный данным возмущением.

Очевидно, что система будет устойчива, если переходные процессы y_п(t), вызванные любыми возмущениями, будут затухающими, т.е. с течением времениy_п(t)будет стремиться к нулю (рисунок 6.1, б).

Решение y_п(t)однородного дифференциального уравнения имеет вид:

, (6.3)

где

C_i- постоянные интегрирования, определяемые начальными условиями и возмущениями;

_i- корни характеристического уравнения:

, (6.4)

Таким образом, переходный процесс y_п(t)представляет собой сумму составляющих, число которых определяется числом корней_i характеристического уравнения (6.4).

В общем случае корни характеристического уравнения являются комплексными, образуя пары сопряженных корней:

, (6.5)

где _i может быть как положительной, так и отрицательной величиной, причем корень вещественный, если_j=0и мнимый, если_i=0.

Каждая пара таких корней определяет составляющую переходного процесса, равную:

, (6.6)

где

иопределяются черези .

Нетрудно увидеть, что эта составляющая представляет собой синусоиду: с затухающими колебаниями, если _i<0; с расходящимися колебаниями, если _i>0; с незатухающими синусоидальными колебаниями при _i=0.

Таким образом, условием затухания данной составляющей переходного процесса является отрицательность действительной части корня характеристического уравнения системы.

Если =0, то процесс определяется только вещественной частью корняи является апериодическим. В общем случае, переходный процесс в системе состоит из колебательной и апериодической составляющих. Если хотя бы один корень имеет положительную действительную часть, он даст расходящуюся составляющую переходного процесса и система будет неустойчива. Отсюда следует, что общим условием затухания всех составляющих, а значит и всего переходного процесса в целом, является отрицательность действительной части всех корней характеристического уравнения системы, т.е. всех полюсов (нулей знаменателя) передаточной функции системы.

Наиболее наглядно вышеизложенное можно проиллюстрировать, если изобразить корни характеристического уравнения на комплексной плоскости (рисунок 6.2). В этом случае найденное выше условие устойчивости можно сформулировать так: условием устойчивости системы является расположение всех корней характеристического уравнения системы, т.е. полюсов передаточной функции системы, в левой комплексной полуплоскости, или, говоря короче, все корни должны быть «левыми». Наличие корня на мнимой оси означает, что система находится на границе устойчивости.

Рисунок 6.2 Изображение корней характеристического уравнения на комплексной плоскости

Итак, на первый взгляд задача исследования устойчивости не представляет затруднений, так как достаточно определить расположение корней характеристического уравнения на комплексной плоскости. Однако определение корней характеристического уравнения, имеющего порядок выше третьего, сопряжено со значительными трудностями, в связи с чем и возникает проблема исследования устойчивости систем, динамические процессы в которых описываются дифференциальными уравнениями высокого порядка.

Частичное решение этой проблемы найдено косвенным путем. Разработан ряд признаков, по которым можно судить о знаках действительных частей корней характеристического уравнения системы и тем самым об устойчивости системы, не решая самого характеристического уравнения. При этом обычно встречаются две постановки задачи исследования устойчивости системы:

1. заданы все параметры системы и необходимо определить, устойчива ли система при этих значениях параметров;

2. необходимо определить значения некоторых параметров (при заданных остальных), при которых система устойчива.

Математическая формулировка условий, которым должны удовлетворять коэффициенты характеристического уравнения или какие-либо функции этих коэффициентов, чтобы система была устойчивой, называется критерием устойчивости.

Критерии устойчивости делятся на алгебраические и частотные. Выделяют три основных критерия устойчивости:

1. Алгебраический (аналитический) критерий устойчивости Рауса-Гурвица;

2. Частотный критерий Михайлова;

3. Частотный критерий Найквиста.