3. Суждение об устойчивости по амплитудным и фазовым характеристикам

Строим их в простом масштабе

.

Переход АФХ отрезка -¥¸1соответствуетq=p=180°иmod|W(j)|=R()>1

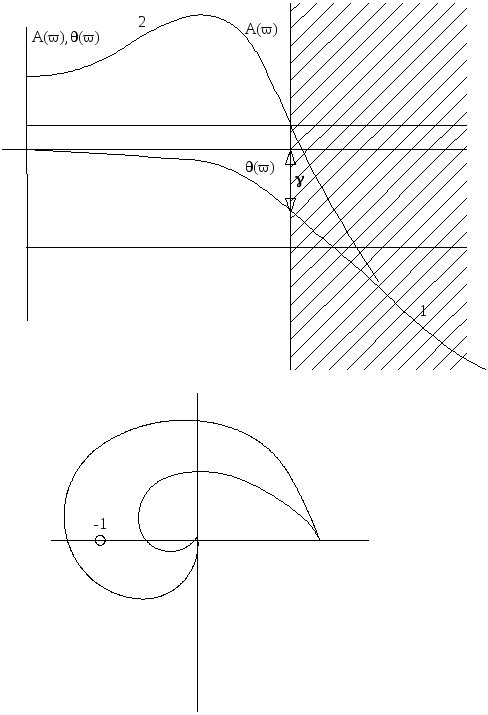
Рисунок 6.21 Амплитудная и фазовая характеристики

Строим характеристики 1 и 2. Положительному переходу соответствует возрастание q, а отрицательному переходу - убываниеq.

Сформулируем правило определения устойчивости по частотным характеристикам: замкнутая система устойчива, если разность между числом переходов фазовой характеристики разомкнутой системы через линию pснизу вверх и числом переходов через эту линию сверху вниз вне заштрихованной области равной k/2, где k-это число правых корней c положительной вещественной частью в характеристическом уравнении разомкнутой системы.

Например:

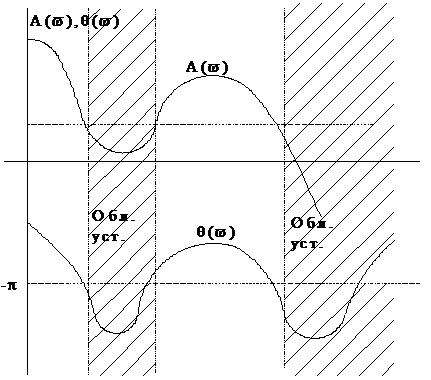
Рисунок 6.22 К примеру определения устойчивости по ЛАХ

Получаем:

положительных переходов в опасной зоне равно 2;

отрицательных переходов в опасной зоне нет;

2-0=2

Вывод: если k=0 - то система неустойчива. Еслиk=4, то- система устойчива.

Об устойчивости системы можно судить и по ЛАХ. Замкнутая САР будет устойчива, если разность между числами положительных и отрицательных переходов фазовой характеристики линии -pравнялось нулю при тех значениях частот, при которых ЛАЧХ положительна.

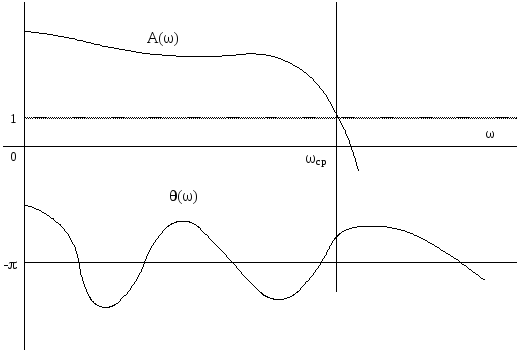
Рисунок 6.23 К примеру определения устойчивости по ФЧХ и ЛАХ

3. Суждение об устойчивости по логарифмическим амплитудным и фазовым характеристикам

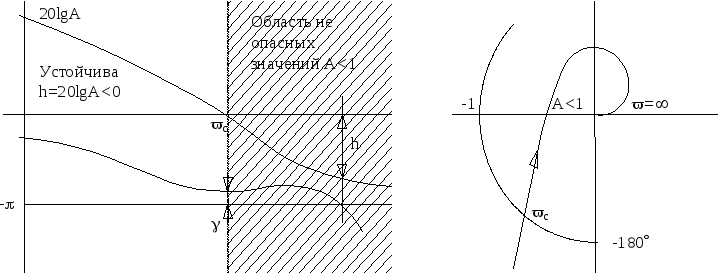
Рисунок 6.24 ЛЧХ условно устойчивой системы:

Замкнутая САР устойчива, если ФЧХ разомкнутой системы пересекает линию -pв области не опасных значений модулей.

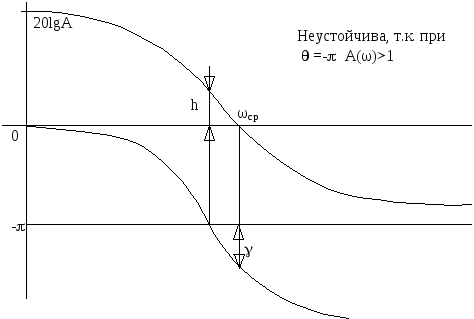
Рисунок 6.25 Пример неустойчивой САУ

3. Влияние параметров системы на ее устойчивость. Исследование сар построением областей устойчивости (d-разбиения)

Пусть имеется характеристическое уравнение замкнутой системы

;.

Для определения того, в каком диапазоне могут меняться параметры a₁…a_nпри устойчивой работе системы, был разработан и усовершенствован (1940 г. А.А. Соколов, 1948 г. Ю. И. Неймарк) метод выделения областей устойчивости.

Пусть имеется – годограф Михайлова на границе устойчивости. Если система находится на границе устойчивости, то годограф МихайловаD(j)проходит через начало координат, что может быть отображено уравнением:

, (6.45)

Выделим в уравнении (6.45) нужные параметры и начертим границу при =0¸¥. Эта граница называетсяD-разбиением и представляет собой отображение границы устойчивости в плоскости корней в плоскости параметров системы.

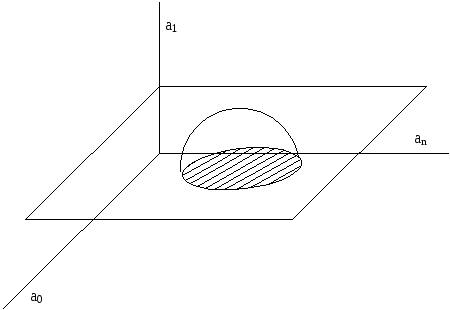
Рисунок 6.26 D-разбиение

Чтобы система была устойчива, необходимо, чтобы все корни характеристического уравнения замкнутой системы были «левыми».

Коэффициенты характеристического уравнения зависят от постоянных времени

и т.д.

Для выяснения характера влияния параметров на устойчивость переносят границу устойчивости из плоскости корней в плоскость параметров. Это делают из условия D_з(j)=0. В этом уравнении выделяют параметры и строят в плоскости параметров границу устойчивости (кривуюD-разбиения).

Граница устойчивости выделяется штриховкой по правилу Неймарка. При движении по мнимой оси от w=-¥доw=+¥штрихуется левая сторона, оставляя область корней с отрицательной вещественной частью слева.

Имеем: - характеристическое уравнение замкнутой системы. Необходимо найти уравнение границы устойчивости, т.е.при-¥<<¥. Зададим, какие параметры будем исследовать, напримерAиB. Выделяем из уравненияD_з(j)AиBи записываем

и.

D-разбиение для одного комплексного параметра.

1)Записываем , т.е. из полиномаD(p)выносят параметрK, аS(p)– полином, не содержащий параметрK.

2)Далее - разделяем на вещественную и мнимую части.

3)Строим зависимость K(), задаваясь различными значениями. Получим границу областей устойчивости.

4) Выделяем области устойчивости штриховкой по Неймарку, для этого:

а) отмечаем направление движения от-¥к+¥;

б) заштриховываем левую часть кривой по отношению к движению.

Вся плоскость разбивается на три зоны (I, II и III) (рисунок 6.27). Часть плоскости, в сторону которой направлены штрихи (I зона) отображает левую полуплоскость корней и поэтому имеет наибольшее количество левых корней и является областью наибольшей устойчивости.

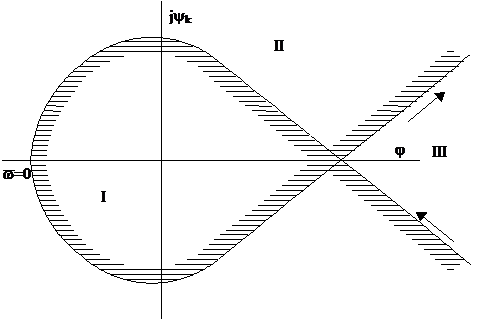
Рисунок 6.27 Граница областей устойчивости.

Переходя из I во II область, т.е. переходя кривую D-разбиения из заштрихованной части в не заштрихованную, теряется один отрицательный и приобретается один положительный корень (корень переходит в правую полуплоскость).

Запас устойчивости уменьшается в III области, где теряется два отрицательных корня.

Итак, область I (рисунок 6.27) имеет наибольший запас устойчивости. Проверяем устойчивость в точке 0. Так как параметр K- вещественный, то находим те значенияK, которые находятся в I области на вещественной оси. При этих значениях САР будет обладать наибольшим запасом устойчивости.

Пример. Характеристическое уравнение замкнутой системы:

,

T₁=0,5 с, T₂=0,1 с, T₃=1 с.

Найдем значение K, соответствующее наибольшей устойчивости.

1. ;

2. ,

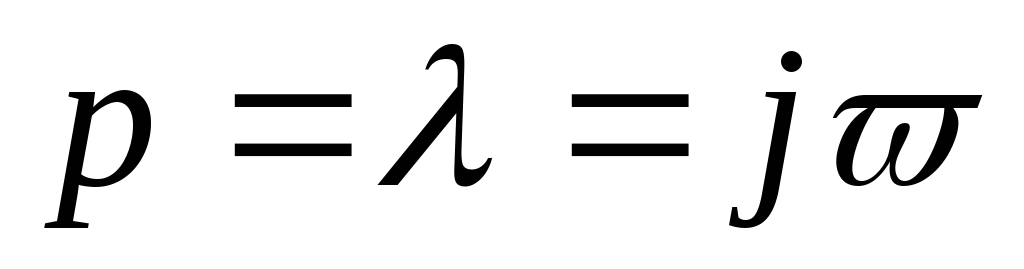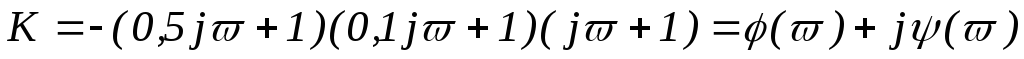где ;

3)строим D-разбиение.

Таблица 6.2

	0	1	2	3	5
φ()	-1	-0,35	1,6	4,85	15,85
ψ()	0	-1,55	2,8	-3,45	-1,75

4)так как параметр k-вещественный, то вещественные значенияk=j()и лежащие на отрезкеAB, т.е. от –1 до 19.8 соответствуют устойчивой работе САР.

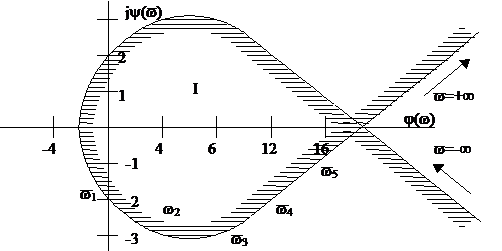
Рисунок 6.28 К примеру определения наибольшей устойчивости замкнутой системы

Часто бывает, что областей с различными областями устойчивости меньше степени характеристического уравнения, а значит и числа корней характеристического уравнения. В таком случае область наибольшей устойчивости дают только запас устойчивости, но не отвечает на вопрос, устойчива ли система, при этом необходимо после выбора параметров исследовать устойчивость другими методами.

Чаще всего это делают при значении параметра равном нулю, т.е. в начале координат кривой D-разбиения.

В нашем характеристическом уравнении положим k=0.

и найдем корни, приравнивающие к нулю все сомножители

т.е.I-я область соответствует устойчивой работе САУ при измененииkот –1 до 19,8, т.е. от 0 до 19,8.

Для определения абсолютного числа отрицательных корней для какого-нибудь частного значения исследуемого параметра надо решить характеристическое уравнение и найти число интересующих нас корней. Обычно величина параметра берется равной нулю (начало координат плоскости параметра). При этом характеристическое уравнение упрощается. В дальнейшем мы определяем число корней во всех зонах с помощью штриховки на кривой D-разбиения.

Выбираем область наибольшей устойчивости и сравниваем количество отрицательных корней с показателем степени nхарактеристического уравнения. Если количество отрицательных корней равноn, то система устойчива.