3. Методы цифрового моделирования систем автоматического управления электроприводами постоянного тока

Методы цифрового моделирования динамических систем основываются на численном интегрировании системы дифференциальных уравнений:

, (11.6)

где xи u - n-мерный вектор переменных состояния и m-мерный вектор управления соответственно;F- n-мерная вектор-функция.

Системы электропривода описываются в основном структурной схемой и для их моделирования применяются соответственно цифровые структурные методы, отличительной особенностью которых является структурно-визуальная минимизация числа блоков схемы и преобразование в детализированную. Ниже рассматривается явный метод структурно-топологического моделирования, основанный на использовании базисных звеньев:

, (11.7)

, (11.8)

где Z(t) - вектор внутренних переменных;

f- скалярная нелинейная функция.

Соотношению (9.7) соответствует интегрирующее звено. Дифференцирующее звено может быть получено из интегрирующего структурным преобразованием по правилу инверсии. Частным случаям безинерционного нелинейного звена (11.8) являются пропорциональное и суммирующее звенья.

В данном базисе система (11.6) представляется в виде совокупности уравнений:

, (11.10)

, (11.11)

где q- число переменных, равное числу звеньев схемы.

Сущность данного метода рассмотрим на примере моделей некоторых типовых звеньев.

1. Интегрирующее звено.

Передаточная функция интегрирующего звена имеет вид

, (11.12)

Структурная схема изображена (рисунок 11.1), вычислительный алгоритм для данного звена можно реализовать в виде, соответствующем следующему выражению

, (11.13)

Рисунок 11.1 Структура интегрального звена

Данному выражению соответствует дискретная модель, (рисунок 11.2), полученная заменой второго блока на детализированное представление.

2. Апериодическое звено первого порядка.

Апериодическое звено первого порядка имеет следующую передаточную функцию:

Рисунок 11.2 Вычислительная структура интегрирующего звена.

(11.13)

Операторное уравнение будет иметь вид

. (11.14)

Выражению (11.14) соответствует структурная схема (рисунок 11.3), которая на основании вышеизложенного преобразуется в вид, представленный на рисунке 11.4.

Рисунок 11.3 Структура апериодического звена

Рисунок 11.4 Дискретная модель апериодического звена

Введение внутренних переменных для каждого элементарного звена позволяет формализовать процесс составления вычислительных соотношений, которые приведены ниже:

(11.15)

3. Пропорционально-интегральное звено.

Звено описывается передаточной функцией вида:

, (11.16)

отсюда следует:

. (11.17)

На основании (11.17) получаем структуру, представленную на рисунке 11.5.

Рисунок 11.5 Структура пропорционально-интегрального звена

Вводя дополнительные переменные, как показано на рисунке 11.6, получим систему уравнений:

, (11.18)

Рисунок 11.6 Вычислительная структура пропорционально-интегрального звена

4. Реальное дифференцирующее звено.

Передаточная функция звена имеет вид:

. (11.19)

Используя выражение передаточной функции, получим:

. (11.20)

Структурная схема данного звена принимает вид, изображенный на рисунке 11.7.

Рисунок 11.7 Структура реального дифференцирующего звена

Разностные уравнения дискретной модели реального дифференцирующего звена:

(11.21)

получены из структуры, приведенной на рисунке 11.8.

Рисунок 11.8 Вычислительная структура дифференцирующего звена

Моделирование систем, содержащих нелинейные безинерционные звенья, не вызывает затруднений. Точность и устойчивость рассмотренного подхода соответствуют численным методам первого порядка. Для сравнительной оценки сложности приведем вычислительные алгоритмы, полученные методом, точность которых определяется только ошибкой дискретной экстраполяции непрерывного входного сигнала.

Сущность известных в настоящее время разностных методов и состоит в замене процессов, происходящих в непрерывных системах, процессами в эквивалентных дискретных системах. Математическим аппаратом при этом служит методz- преобразования.

Как видно из рисунка 11.9, эквивалентная дискретная система имеет синхронно работающие идеальные импульсные элементы на входе и выходе непрерывной части и формирующий элемент, представляющий собой линейный непрерывный элемент с передаточной функцией W_ф(p). Формирующий элемент и непрерывная часть образуют совместно приведенную непрерывную часть (ПНЧ).

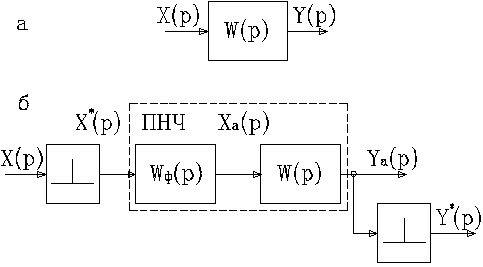
Рисунок 11.9 Структура эквивалентной дискретной системы

Новая величина Y_a(t)на выходеW(p)будет приближенной величиной фактического выходаY(t). Прерывание и экстраполяция являются чисто условными математическими операциями при анализе непрерывных систем. При выбранном шаге по времениTстепень приближения может быть изменена путем выбора передаточной функции формирующего элементаW_ф(p).

Основное соотношение между числами X^*(t)иY_a^*(t)или междуz-преобразованиямиX(z)иY_a(z)можно теперь получить для любой передаточной функции непрерывной системы:

, (10.22)

где W(z)- дискретная передаточная функция, соответствующая передаточной функции ПНЧW_ф(p)W(p).

Для непрерывных систем с постоянными сосредоточенными параметрами передаточные функции эквивалентных дискретных систем обычно удается найти в замкнутой форме в дробно-рациональном виде:

, (11.23)

где W(p)- передаточная функция формирующего элемента.

Произведя идентификацию дискретной передаточной функции (11.23), приходим к следующему разностному алгоритму формирования дискретных значений выходного сигнала:

. (11.24)

В предложенных к настоящему времени разностных методах решения дифференциальных уравнений выражения для дискретной передаточной функции W(z)получают непосредственно из рассмотрения различных видов формирующих элементов, а также другими путями.

Рассматриваемый подход применим к линейным системам автоматического управления, как с запаздыванием, так и без него, а также может быть распространен на замкнутые нелинейные системы и системы с переменными параметрами.

В качестве формирующего элемента в этом методе используется экстраполятор нулевого порядка с передаточной функцией:

. (11.25)

В этом случае сигнал x_a(t)на входе звенаW(p)есть ступенчатая аппроксимация исходного входного сигнала x(t). Дискретная модель системы запишется при этом в виде:

. (11.26)

Нетрудно убедиться, что при T0наблюдается предельный переходW(z)W(p). Действительно, приT0имеем(z-1)/zpT, аTZ{W(p)/p}стремится кW(p)/p, откуда и следует доказываемое асимптотическое соответствие.

Полюсами цифровой модели являются величины z_i=e^p_i^T, гдеp_i- полюса передаточной функцииW(p).

Таким образом, устойчивой непрерывной системе соответствует устойчивая цифровая модель.

Данный метод требует отыскания передаточной функции W(z)дискретной системы по заданной передаточной функции непрерывной системы.

Дискретная передаточная функция системы невысокого порядка отыскивается сравнительно легко. При нахождении дискретных передаточных функций системы высокого порядка встречаются значительные трудности, связанные с необходимостью проведения большого объема вычислений с высокой степенью точности. В этих случаях обычно рекомендуется находить дискретную передаточную функцию всей системы по дискретным передаточным функциям ее отдельных звеньев, пользуясь при этом обычными правилами получения передаточной функции системы для различного соединения ее звеньев.

Типовые звенья, такие как интегрирующее, апериодическое, реальное дифференцирующее, при преобразовании их в дискретную форму примут следующий вид:

1) Интегрирующее звено:

Применяя к (11.12) формулу (11.26), получим:

, (11.27)

где .

Применяя к (11.27) обратное z-преобразование, найдем.

Поскольку период квантования в цифровых системах и шаг интегрирования tпри моделировании систем классическими методам интегрирования - по сути своей одно и то же, то можно сделать вывод о полном соответствии разностных уравнений интегрирующего звена в обоих методах.

2) Апериодическое звено:

Применяя к выражению (11.13) формулу (11.26), получаем следующий вид z-передаточной функции для апериодического звена:

, (9.28)

где ;

и, применяя к (11.28) обратноеz-преобразование, получим:

.

3) ПИ-регулятор :

Преобразуя (11.16) по (11.26), получим:

, (11.29)

где . Производя обратноеz-преобразование соотношения (11.29), найдем .

Реальное дифференцирующее звено описывается следующей передаточной функцией:

, (11.30)

где ;

.

Применяя формулу (11.26) к (11.36), как и в предыдущих случаях, получим:

(9.31)

где ;

;

.

Возьмем обратное z-преобразование и получим следующее разностное уравнение:.

Рассмотренный выше метод является универсальным в том смысле, что может быть произвольно использован при входных сигналах аналитической или произвольной формы и применим к любым системам автоматического управления, при этом отдельные части системы могут быть заданы экспериментальными данными, представленными в табличной или графической форме.

Алгоритмы при цифровом моделировании одной и той же системы получаются одинаковыми по сложности: порядок разностного уравнения совпадает с порядком линейной части моделируемой системы.

Анализируя приведенные выше методы, можно дать следующие рекомендации относительно их применений. Метод моделирования на основе структурно-топологических представлений достаточно прост, при его применении требуется небольшая подготовительная работа, он характеризуется малым объемом вычислений из совокупности классических методов решения дифференциальных уравнений. К недостаткам метода можно отнести невысокую точность, необходимость задания шага порядка 0,1-0,2 наименьшей постоянной времени, исходя из условий получения достоверного решения. Метод, основанный на замене непрерывных сигналов их дискретными аппроксимациями, при необходимости моделирования звеньев порядка выше первого (исключая звенья второго порядка, у которых 1) связан с необходимостью выполнения достаточно большой подготовительной работы, при этом данный метод, как правило, требует знания информации о значениях переменных на предыдущих шагах. Представление идеального интегрирующего звена в обоих методах одинаково, в результате чего можно сделать вывод о предпочтительности метода моделирования, основанного на структурно-топологических представлениях для моделирования данного класса систем управления.

Структурно-топологический метод предпочтителен при синтезе управлений в автоматическом электроприводе с применением программных контроллеров, имеющих ограниченные ресурсы по памяти, быстродействию и математическому обеспечению.

На основании изложенного выше метода, основанного на структурно-топологических представлениях, может быть предложена следующая методика исследования моделей систем управления электроприводами.

1. Система автоматизированного электропривода описывается структурной схемой, типовые звенья которой отражают физические устройства.

2. Проводится детализация звеньев и структуры системы через базисный набор звеньев (интегрирующих и нелинейных) с минимизацией их числа.

3. Структурная схема преобразуется в алгоритмическую заменой интегрирующих звеньев на цифровые модели.

4. По алгоритмической структуре составляется алгоритм, а затем и программа на выбранном языке программирования.