>
8x1 |
1 |
+2x2 |
2 |
5x3 |
3+ x44 |
2 = 0 |
II |
||
2x |
|
|
3x |
|
4x + x |
|
3 = 0 I |
||
> |
|
|
|
|
1 = 0 |
III |
|||
>5x1 |
|
3x2 |
+ x3 |
4x4 |
|
||||
> |
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
>
>
:10x1 + 2x2 x3 + 2x4 + 4 = 0 IV
Систему следует привести к виду, пригодному для применения метода итерации:
8
>10x1 + 2x2 x3 + 2x4 + 4 = 0
>
>
<x1 5x2 x3 + 0x4 1 = 0
>x1 2x2 + 5x3 x4 2 = 0
>
>
:3x1 + 0x2 0x3 + 9x4 10 = 0
Второе у-ние получим как разность I и II, четвертое у-ние получим, как линейную комбинацию: 2I II + 2III IV . Для решения этой системы можно использовать метод итерации.
8.3Метод Зейделя
Итерационный метод Зейделя имеет вид
(k+1) |
|
i 1 aij (k+1) |
n |
aij (k) |
|
bi |
||||
|
= |
jP |
|
|
j=Pi+1 |
|
|
|
|
|
xi |
|
aii xj |
+ aii i = 1; :::; n k = 0; 1; ::(1) |
|||||||
=1 aii xj |
|
|||||||||
В качестве пояснения запишем подробно первые два уравнения системы (1)
|
(k+1) |
n |
a1j |
(k) |
|
|
b1 |
|
|
|
||
|
x1 = |
jP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a11 |
(2) |
|
||||||
|
=2 a11 xj |
|
|
|||||||||
(k+1) |
a21 (k+1) |
|
n |
a2j |
(k) |
|
b2 |
|||||
|
= a22 x1 |
|
|
jP |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
+ a22 (3) |
|||||
|
=3 a22 xj |
|||||||||||
Примечания. Систему у-ний (1) можно записать по иному, например
(
|
ij = |
aij |
i 6= j |
|
|
|
|
|
aii |
i = |
bi |
i; j = 1; :::n |
|||
|
aii |
||||||
|
ij |
= 0 |
|
i = j |
|
|
|
|
|
|
|
|
|||
тогда система (1) преобразуется к виду |
|
|
|
|
|||
(k+1) |
|
i 1 |
(k+1) |
n |
|
(k) |
|
xi |
= i + |
jP |
|
P |
|
|
|
=1 ijxj j=i+1 ijxj i = 1; 2; :::; n (4) |
|||||||
8.3.1Сходимость метода Зейделя (первое достаточное условие)
Теорема. Если для линейной системы
x = + x (5)
выполняется условие
jj jjm < 1
где
|
n |
|
jP |
jj jjm = maxi |
=1jaijj |
то процесс Зейделя для системы (5) сходится к единственному ее решению при любом выборе начального вектора x(0) (без док-ва)
25
8.3.2Оценка погрешности приближенного процесса Зейделя по m-норме
Погрешность приближения по m-норме определяется неравенством
jjx x(k)jjm 6 (1 mm) jjx(k) x(k 1)jj (12)
где
m = max( |
n |
) |
|
m |
jPn |
|
|||
|
=1jaijj |
6 jj |
jj |
|
i |
jP |
|
||
|
1 =1jaijj |
|
|
|
Практически итерационный процесс прекращается, если выполняется неравенство
max jx(ik) x(ik+1)j < "
16i6n
где " заданная погрешность, или задается максимальное число итераций.
26
Часть III
Численные методы решения систем нелинейных уравнений
Пусть дана система нелинейных уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
8f2 |
(x1 |
; x2 |
; :::; xn) = 0 |
|
|
||||||||
f1 |
(x1 |
; x2 |
; :::; xn) = 0 |
|
|
||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
>::: |
|
|
|
|
|
|
|
|
|
|
|
|
|
>fn(x1; x2; :::; xn) = 0 |
|
||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
С действительными левыми частями.: |
|
|
0x21 f = |
0f21 |
|||||||||
x = |
|||||||||||||
|
|
|
|
|
x1 |
|
|
|
|
f1 |
|
||
|
|
|
|
Bx |
|
C |
|
|
Bf |
|
C |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||
|
|
|
|
B |
|
nC |
B |
|
nC |
||||
|
|
|
|
@ |
::: |
A |
@ |
::: |
A |
||||
|
|
|
|
|
|
|
|
||||||
Система (1) кратко записывается как
0 f(x) = 0 (1 )
Для решения системы (10) воспользуемся методом последовательного приближения. Предположим, что найдено приближение с номером p
0 1
x(1p)
x(p) = Bx(2p)C
B C
B ... C @ A
x(np)
одного из корней системы (10). Тогда каждый корень можно представить в виде
x = x(p) + h(p) (2)
где
|
(p) |
0h2(p) |
1 |
|
|
|
= B |
h1(p) |
C |
h |
::: |
|||
|
|
B |
|
C |
|
|
B |
|
C |
|
|
@ |
hn(p) |
A |
|
|
|
|
|
поправка для приближенного корня. Подставляя (2) в (10) получим
|
|
|
(p) |
|
|
(p) |
|
(3) |
|
|
|
|
|
||||
f(x |
+ h |
|
||||||
|
|
) = 0 |
||||||
Предположим, что ф-и f1; f2; :::; fn имеют непрерывные частные производные в некоторой области, содержащей x и x(p) . Тогда (3) по формуле Тейлора получится
|
|
|
(p) |
|
|
(p) |
|
|
|
(p) |
|
|
0 |
|
(p) |
|
(p) |
|
|
|
|
|
|
|
|
|
|
||||||||||
f(x |
|
(4) |
||||||||||||||||
|
+ h ) = f(x |
|
) + f (h |
) h |
= 0 |
|||||||||||||
В развернутом виде (4) выглядит так:
f1(x(1p) + h(1p); x(2p) + h(2p); :::; x(np) + h(np)) = f1(x(1p); x(2p); :::; x(np)) + f10x1 (x(1p); x(2p); :::; x(np)) h(1p) + f10x2 (x(1p); x(2p); :::; x(np)) h(2p) + . . . + f10xn (x(1p); x(2p); :::; x(np)) h(np) = 0
27
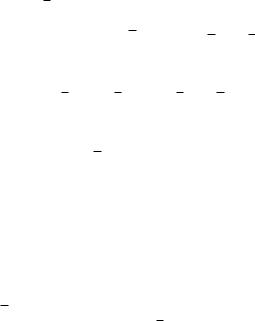
f2(x(1p) + h(1p); x(2p) + h(2p); :::; x(np) + h(np)) = f2(x(1p); x(2p); :::; x(np)) + f20x1 (x(1p); x(2p); :::; x(np)) h(1p) + f20x2 (x(1p); x(2p); :::; x(np)) h(2p) + . . . + f20xn (x(1p); x(2p); :::; x(np)) h(np) = 0
...
fn(x(1p) + h(1p); x(2p) + h(2p); :::; x(np) + h(np)) = fn(x(1p); x(2p); :::; x(np)) + fnx0 1 (x(1p); x(2p); :::; x(np)) h(1p) +
fnx0 2 (x(1p); x(2p); :::; x(np)) h(2p) + . . . + fnx0 n (x(1p); x(2p); :::; x(np)) h(np) = 0
Из (4) следует, что матрица Якоби |
0 |
|
|
|
|
1 |
||||||
|
f0(x) = w(x) = |
@x1 |
@x2 |
::: |
@xn |
|||||||
|
|
|
|
|
|
|
|
@f1 |
@f1 |
::: |
@f1 |
|
|
|
|
|
|
|
|
|
@x1 |
@x2 |
@xn |
|
|
|
|
|
|
|
|
|
|
@f2 |
@f2 |
|
@f2 |
|
|
|
|
|
|
|
|
B |
@fn |
@fn |
::: |
@fn C |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
B |
::: |
::: |
::: |
C |
|
|
|
|
|
|
|
|
B |
@x1 |
@x2 |
|
@xn C |
|
|
|
|
|
|
|
|
@ |
|
|
|
|
A |
Теперь (40) можно записать как
|
|
|
(p) |
|
|
(p) |
|
|
(p) |
|
|
|
|
|
|
|
|||||
f(x |
) + w(x |
)h = 0 |
||||||||
Полагая, что матрица w(x(p)) невырожденная получим
h(p) = w 1(x(p))f(x(p))
следовательно
x(p+1) = x(p) w 1(x(p))f(x(p)) p = 0; 1; 2; ::: (5)
Пусть " требуемая точность. Процесс итерации (5) завершается, когда выполняется неравенство
jh(ip)j < " i = 1; 2; :::; n p = 0; 1; 2::: (6)
либо число итераций заранее задано.
Примечание. Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы. Практически метод Ньютона применяется для уточнения решения полученного какимлибо другим методом.
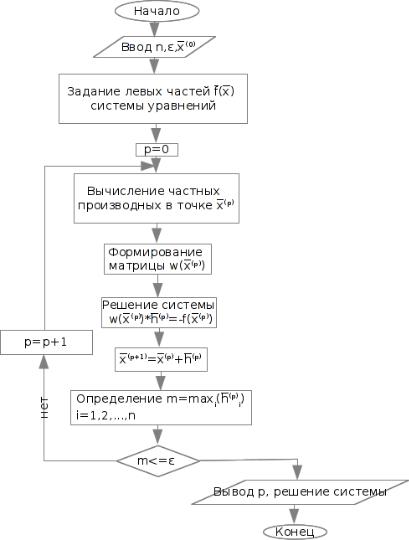
9Блок-схема алгоритма метода Ньютона
Входные параметры: x(0) вектор начальных приближений, n число уравнений, " погрешность, f(x) левые части уравнений Выходные параметры: x вектор решений, p число итераций
28
29