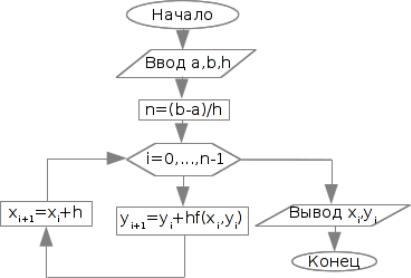
27.2Блок-схема алгоритма метода Эйлера

Входные параметры: a,b,h,x0 = a,y0 = y(x0) Выходные параметры: xi,yi

27.3Применимость метода Эйлера к системам дифференциальных у-ний

Метод Эйлера распространяется на системы дифференциальных у-ний и на дифференциальные у-ния высших порядков. Последние должны быть предварительно приведены к нормальной системе дифференциальных у- ний. Рассмотрим нормальную систему двух дифференциальных у-ний

(

y0 = f1(x; y; z)

(5)

z0 = f2(x; y; z)

с начальными условиями

y(x0) = y0 z(x0) = z0

Приближенные значения вычисляются по формулам

(

yi+1 = yi + hf1(xi; yi; zi) i = 0; 1; 2; ::: (6) zi+1 = zi + hf2(xi; yi; zi)

28 Метод Рунге-Кутта

Пусть дано дифференциальное у-ние

y0 = f(x; y) (1)

с начальным условием

y(x0) = y0

Пусть h - шаг

xi = x0 + ih i = 0; 1; 2; :::

Рассмотрим числа

62

		K1(i) = hf(xi; yi)
	8K(i)		= hf(xi + h		; yi +	K1(i)	)
	>	(i)		2		(i)
	>			h		K2
	>
	>K3		= hf(xi +		; yi +		)
				2		2
	<	2
						2
	>K4(i) = hf(xi + h; yi + K3(i))

>

>

>

:

Согласно методу Рунге-Кутта последовательные значения yi искомой ф-и определяются по формуле

yi+1 = yi + yi

где

yi = 16 (K1(i) + 2(K2(i) + K3(i)) + K4(i)) i = 0; 1; 2; :::(3)

Так же называется методом Рунге-Кутта четвертого порядка точности. Обладает значительной точностью. Применим для приближенного решения систем обыкновенных дифференциальных уравнений.

Пусть дана система:

@y

= f(x;

) (4)

y

@x

и начальные условия

(x0) =

0

y

y

Задавшись шагом h и введя обозначения

xi = x0 + ih

(xi) =

i

y

y

i+1

yi =

0

y

y

получим систему

8K

2(0)

= hf(xi + h2 ; y0 + K21

)

1(0)

>

K

= hf(xi;

y

0)

(5)

h

(i)

>

K2

>

(i)

>

K

= hf(xi +

;

0

+

)

3

y

2

2

<

(0)

>

>K

4(0) = hf(xi + h; y0 + K3(i))

>

>

>

>

Согласно методу Рунге-Кутта

:

1 (

(i)

+ 2(

(i) +

(i)) +

(i)) (6)

y

0

=

K

K

K

K

6

1

2

3

4

Отсюда находим

y1 = y0 + y0

Далее, приняв (x1; y1) за исходные данные и повторяя то же самый процесс находим y2, аналогично и так далее.

63

Часть VIII

Аппроксимация ф-и

29 Постановка задачи об апроксимации ф-и

Пусть на некотором множестве задана система ф-ий

f0(x); f1(x); :::; fm(x); :::

которые в дальнейшем будем считать достаточно гладкими ф-ями. Например, непрерывно дифферернцируемыми. Назовем эту систему основной. Ф-и вида

Qm(x) = c0 0(x) + c1 1(x) + ::: + cm m(x) (1)

где c0; c1; :::; cm называются обобщенными полиномами порядка m. В частности, если

0(x) = 1

0(x) = x

...

0(x) = xm

то

Qm(x) = c0 + c1x + c2x2 + ::: + cmxm

есть обычный полином степени m.

Задача о приближении ф-и ставится так: данную ф-ю f(x) требуется заменить обобщенным полиномом Qm(x) заданного порядка m так, чтобы отклонение (в известном смысле) ф-и f(x) от обобщенного полинома Qm(x) на указанном множестве X = fxg было наименьшим. При этом в общем случае Qm(x) называется аппроксимирующим.

Если множество X состоит из отдельных точек, то приближение называется точечным. Если же множество X есть отрезок a 6 x 6 b, то приближение называется интегральным. Термин отклонение двух ф-ий в зависимости от обстоятельств понимается по разному, при этом получают различные типы задач теории приближений:

1.интерполирование;

2.среднее квадратичное приближение;

3.равномерное приближение

4.и д.р.

30 Системы ф-ий, ортогональные на интервале

Определение. Система интегрируемых ф-ий

0(x); 1(x); 2(x); :::; n(x) (1)

называется ортогональной на [a; b] если

a

( m; n) = m(x) n(x)dx = 0 m 6= n

b

jj m(x)jj =	( m; n) s
			b	m2	(x)dx m 2 [a; b]
p			a

64

b i=0

Если все нормы равны 1, то система называется ортонормированной, для которой выполняется условие:

a

m(x) n(x)dx = mn

b

где

(

mn =

0 m 6= n

1 m = n

Всякую систему, несодержащую ф-ю с нулевой нормой можно нормировать. Для этого достаточно каждую ф-ю разделить на ее норму. Пусть f(x) - ф-я, определенная на [a; b] и

Qm(x) = c0 0(x) + c1 1(x) + ::: + cm m(x) (2)

обобщенный полином.

В выражении (2) c0; c1; :::; cm - постоянные коэффициенты.

Рассмотрим задачу о приближении ф-и f(x). Требуется данную ф-ю заменить обобщенным полиномом Qm(x) заданного порядка m так, чтобы отклонение в смысле предъявленного критерия ф-и f(x) от обобщенного полинома Qm(x) на отрезке [a; b] было наименьшим. Пусть критерием приближения является минимум величины

a

Im = [Qm(x) f(x)]dx ! min (3)

b

Такая задача называется задачей интегральной квадратичной аппроксимации ф-и на отрезке. Подставим в (3) выражение (2) для полинома Qm(x) получим

a m

Im = [Pci i(x)dx f(x)]2dx (4)

b i=0

Для определения коэффициентов ci имеем

1 @Im	a	m
	=	2	j(x)dx = 0 j = 0; 1; :::; m (5)
2 @cj		[Pci i(x) f(x)]

После упрощения система (5) примет вид

m a	a

P

ci i(x) j(x)dx = f(x) j(x)dx (6)

i=0 b

b

В силу ортогональности f i(x)g выполняются следующие равенства

a

i(x) j(x)dx = 0

b

Поэтому

aa

cj Q2j (x)dx = f(x) j(x)dx

bb

Полагаем, что среди i(x) нет ф-ий с нулевой нормой, получим, что

a

f(x) j(x)dx

cj =	b			(7)
		a
		Q2(x)dx
		j
		b
В знаменателе (7) стоит квадрат нормы j(x) поэтому
	a
	f(x) j(x)dx
cj =	b			(8)
		jj j(x)jj2

65

В случае ортонормированной системы

a

cj = f(x) j(x)dx (9)

b

Коэффициенты (8) - коэффициенты Фурье ф-и f(x) относительно заданной ортогональной системы. Доказано, что обобщенный полином с коэффициентами Фурье данной ф-и обладает наименьшим квадратичным отклонением от этой ф-и по сравнениею со всеми другими полиномами порядка m.

Найдем оценку отклонения (4) для случая, когда ci являются коэффициентами Фурье. Имеем

Im

b

m

b

m

m

i2(x) + 2 cick i(x) k(x)]dx

= [f(x) ci i(x)]2dx = [f2

(x) 2f(x) ci i(x) +

ci2

P

P

P

P

a

i=0

a

i=0

i=0

i<k

Переходя от интеграла суммы к сумме интегралов, получим

Im =

b

(x)dx 2

m

b

m

b

(x)dx + 2

cick

b

f2

ci

f(x) i(x)dx +

ci2

i2

i(x) k(x)dx (10)

P

P

P

a

i=0

a

i=0

a

i<k

a

Так как

bb

f(x) i(x)dx = ci 2i (x)dx i = 0; 1; 2; :::

aa

и

b

i(x) k(x)dx = 0 при i 6= k

a

то, после приведения подобных слагаемых в формуле (10) получим:

bm b

Im = f2(x)dx Pc2i 2i (x)dx (11)

a

i=0 a

или

m

Im = jjf(x)jj2 Pc2i jj (x)jj2 (12)

i=0

Так как Im > 0, то из формулы (12) получается так называемое неравенство Бесселя.

m

Pc2i jj (x)jj2 6 jjf(x)jj2 (13)

i=0

В частности при m ! 1 получаем

1

Pc2i jj (x)jj2 6 jjf(x)jj2

i=0

Если система 0(x); 1(x); :::; m(x); ::: ортонормирована, то формулы (12) (13) упрощаются и имеют вид:

m

Im = jjf(x)jj2 Pc2i (14)

i=0

m

Pc2i 6 jjf(x)jj2 (15)

i=0

Обобщенный полином Qm(x) с коэффициентами Фурье обладает следующими важными свойствами:

1.При увеличении числа слагаемых m младшие коэффициенты cj, как следует из формулы (8) остаются неизменными.

b

2. При увеличении m квадратичная погрешность Im = [Qm(x) f(x)]2dx в силу формулы (11) монотонно

a

убывает. То есть погрешность I1 > I2 > ::: > Im > Im+1 > ::: Это означает, что присоединение новых слагаемых увеличивает точность апроксимации.

66