10.1Метод Данилевского

Сущность метода Данилевского заключается в приведении характеристического определителя к нормальному виду Фробениуса.

		1		0		:::	0
D( ) =		p1	p2	:::		:::	pn			(1)
		0	1			:::	0
		0	0	0		:::
		:::	:::	:::		:::	:::

Разложим определитель (1) по элементам первой строки

D( ) = (p )( )n 1 p2( )n 2 + p3( )n 3 . . . pn = ( 1)n ( n p1 n 1

(2)

Обозначим

		a11		a12	:::	a1n	1
A =	0a21			a22	:::	a2n		- заданная матрица
	Ba		n1	a	:::	a	C
	B			n2	:::	nnC
	@	:::		:::		:::	A

01

	B	p1	p2	:::	pn 1	pn	C
P =		0	0	:::	1	0		- матрица Фробениуса, подобная
	B	:::	:::	:::	:::	:::	C
	@						A

P = S 1AS

p2 n 2 p3 n 3 . . . pn)

матрице A

где S невырожденная матрица.

Так как подобные матрицы имеют равный характеристический полином, то

det(A E) = det(p E) (3)

Покажем, каким образом исходя из матрицы A строится матрица P . По методу Данилевского переход от матрицы A к матрице P осуществлется с помощью n 1 преобразования подобия, последовательно преобразующих строки матрицы A, начиная с последней в соотвествующие строки матрицы P . Рассмотрим начало процесса.

Необходимо последнюю строку an1; an2; :::; an;n 1; annперевести в строку 0; 0; :::; 1; 0. Предполагая, что an;n 1 6= 0 разделим все элементы n 1 столбца матрицы A на an;n 1, тогда n-ая стока примет вид an1; an2; :::; 1; ann. Затем вычтем n 1 столбец преобразованной матрицы, умноженный на соотвествующие числа an1; an2; :::; ann

из всех столбцов матрицы, тогда последняя строка примет вид 0; 0; :::; 1; 0.

Указанные операции являются элементарными операциями над столбцами матрицы A. Произведя те же преобразования над единичной матрицей получим

0

0

1

:::

0

0

1

= Bm

1

0

:::

0

0

C

Mn 1

n 1;1

m

n 1;2

:::

m

m

B

:::

n 1;n 1

n 1;nC

B

:::

:::

:::

:::

C

0

0

:::

0

1

B

C

где

@

A

(mn

1;n

1

=

1

i = n 1

(4)

mn 1;i =

ani

i 6= n 1

an;n 1

an;n 1

Отсюда следует, что произведенные операции равносильны умножению справа матрицы Mn 1на матрицу

A

31

	0	b21		b22	:::	b2;n 1		b2n	1
	= B = Bb	b11		b12	:::	b1;n 1		b1n	C(5)
AMn 1		:::	b	:::	:::	b	b
	B n 1;1			n 1;2	:::	n 1;n 1		n 1;nC
	B	0		0		:::		:::	C
					:::	1		0
	B								C
	@								A

Используя правила умножения матриц находим, что элементы матрицы B вычисляются:

(bi;n 1 = ai;n 1mn 1;n 1	j = n 1		6		6
bij = aij + ai;n 1mn 1;;j	j 6= n 1	1		i		n (6)

Но матрица B не подобна матрице A. Для преобразования подобия нужно обратную матрицу Mn 11умножить слева на матрицуB

		Mn 11AMn 1 = Mn 11B
Непосредственной проверкой можно убедиться, что									1
1		0	0	1	:::	0		0
			1	0	:::	0		0
Mn 1	=	Ba:::		a:::	:::	a	a		C	(7)
		B n1		n2	:::	n;n 1		nnC
		B	0	0		:::	:::		C
					:::	1		0
		B							C
		@							A

Обозначим

Mn 11B = C = Mn 11AMn 1 (8)

Умножение слева матрицы Mn 11 на матрицу B не изменяет преобразованной строки (в данном случае

последней) матрицы B. Поэтому матрица имеет вид:

1

0

c21

c22

:::

c2;n 1

c2n

Bc

c11

c12

:::

c1;n 1

c1n

C

C =

:::

c

n 1;2

:::

c

n 1;n 1

c

(9)

B n 1;1

:::

n 1;nC

B

0

:::

:::

:::

C

0

:::

1

0

B

C

@

A

Перемножая Mn 11(формула 7) и матрицу B (формула 5) находим, что

8c

=

n

a

b

i = n

1

1 6 j 6 n (10)

<

cij

= bij

1

6 i

6 n

2

n 1;j

k=1

nk kj

:

P

Умножение матрицы Mn 11 на B меняет лишь n 1 строку матрицы B. Элементы этой строки могут быть найдены из системы (10)

Матрица C A и имеет одну приведенную строку. На этом заканчивается первый этап процесса приведения. Прододжая этот процесс получим матрицу Фробениуса.

P = M1 1M2 1M3 1:::Mn 12Mn 11AMn 1Mn 2Mn 3:::M3M2M1 (100)

Если все n 1 промежуточных преобразований возможны.

32

10.1.1Исключительные случаи метода Данилевского

Допустим, что при преобразовании матрицы A в матрицу Фробениуса P после нескольких шагов пришли к матрице вида:

0d21		d22	:::	:::	::: d2;n 1		d2n		1
	d11	d12	:::	:::	::: d1;n 1		d1n
Bd		d	:::	d	:::	d	d		C
D = B k1		k2	:::	kk	:::	k;n 1		knC
B	:::	:::		:::		:::	:::		C
	0	0	:::	1	:::	0	0
B									C
B	0	0	:::	0	:::	0	0		C
B									C
B									C
B	0	0	:::	0	:::	1	0		C
B	:::	:::	:::	:::	:::	:::	:::		C
B									C
@									A

причем оказалось что dk;k 1 = 0

Тогда продолжать преобразование по методу Фробениуса нельзя.

1.Пусть какой-либо элемент матрицы D стоящий левее 0-ого элемента dk;k 1отличен от 0 т.е. dkL 6= 0 L < k 1. Тогда этот элемент выдвигаем на место dk;k 1 т.е. переставляем k 1 и L-ый столбцы матрицы D и одновременно переставляем ее k 1 и L-ую строку (для сохранения подобия). Можно показать, что новая матрица подобна D и мы можем продолжать метод Фробениуса.

2.Пусть dkL = 0 при L = 1; 2; :::; k 1, тогда матрица D будет иметь вид

0

d11

d12

:::

d1;k

1

d1k

:::

d1;n

1

d1n

1

:::

:::

:::

:::

:::

:::

:::

:::

D = B

0

0

:::

0

d

kk

:::

d

d

kn

C

=

D1

L

B

dk 1;1

dk 1;2

:::

dk 1;k 1

k;n 1

C

0

D

B

dk 1;k

::: dk 1;n 1

dk 1;n

C

2

0

0

:::

0

1

:::

0

0

B

C

B

C

B

0

0

:::

0

0

:::

1

0

C

B

:::

:::

:::

:::

:::

:::

:::

:::

C

B

C

@

A

В этом случае хар-ий определитель распадается на 2:

det(D E) = det(D1 E) det(D2 E)

При этом матрица D2уже приведена к канонической форме Фробениуса. Остается применить метод Данилевского к матрице D1.

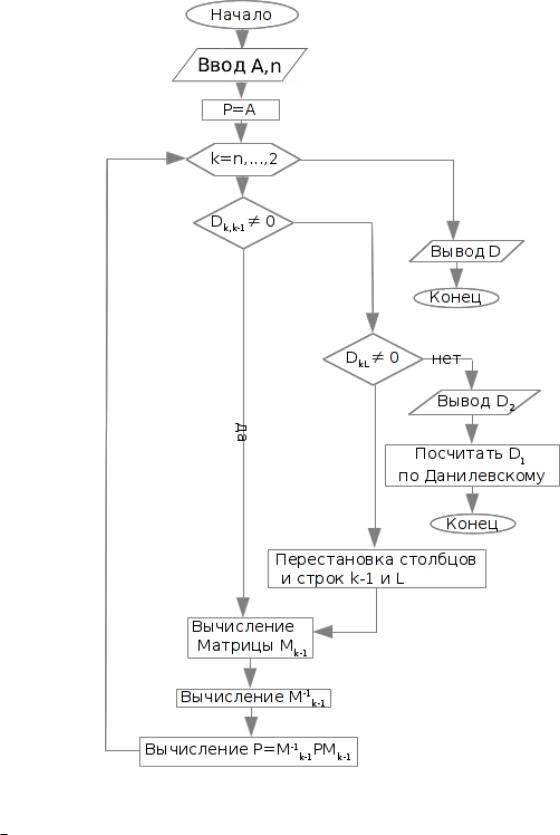
10.1.2Блок-схема построения матрицы Фробениуса

Входные данные. n - размер, A - исходная матрица

Выходные данные: P - матрица Фробениуса, D1; D2 - при исключительном случае.

33

10.1.3Вычисление собственных векторов по Данилевскому

Пусть - собственное значение матрицы A, а значит и подобной ей матрице P . Найдем собственный вектор y соотвестующий матрице P

34