3.5Условия окончания процесса итерации

Пусть погрешность вычисления корня в соотвествии с условиями (14 17). Тогда окончание процесса вычисления должно быть

1 q q j'(x0) x0j < "(18)

1 q q jxn xn 1j < " (19)

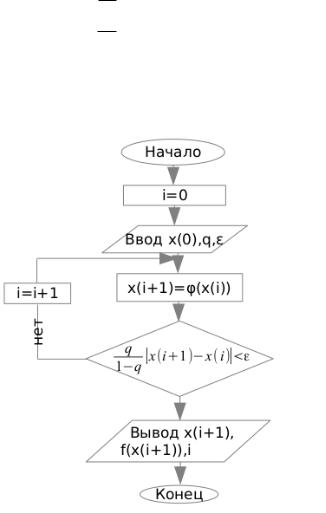
3.6Блок-схема метода итерации

Входные данные: x(0); q; "

Выходные параметры: ; f( ); i + 1

4Метод Ньютона (метод касательных)

Пусть дано у-ние

f(x) = 0 (1)

единственный корень на отрезке [a; b] и производные f0(x), f00(x) непрерывны и сохраняют определенные знаки на [a; b].

Пусть xn какое-либо n-ое приближение корня

xn

на [a; b], уточним его

= xn + hn (2)

где hn - малая величина.

0 = f(xn + hn) f(xn) + f0(xn) hn

11

hn = f0(xn) f (xn)

подставив это значение hn в формулу (2) получим следующее приближенное значения корня

xn+1 = xn f0(xn) n = 0; 1; 2; ::: (3)

f (xn)

4.1 Геометрическая интерпретация метода Ньютона

Положим для определенности при x 2 [a; b].

f00(x) > 0 f(b) > 0

Выберем x0 = b, тогда

f(x0) > 0 и f00(x0) > 0

Проведем касательную к графику ф-и y = f(x) в точку B0(x0; f(x0)), ее уравнение имеет вид f(x0) y = f0(x0)(x0 x)

или

y f(x0) = f0(x0)(x x0)

В качестве первого приближения x1 корня возьмем абсциссу точки пересения этой касетельной с осью Ox, т. е. положим

y = 0 x1 = x0 f0(x0) f (x0)

Через точку B1(x1; f(x1)) снова проведем касательную. В качестве второго приближения x2 корня возьмем абсциссу точки пересечения этой касательной с Ox и т. д.

На n-ом шаге у-ние касательной будет иметь вид

y f(xn) = f0(xn)(x xn)

Полагая в нем

y = 0 x = xn+1

получим формулу

xn+1 = xn f0(xn) (3) f (xn)

12

4.2Сходимость итерационного процесса в методе Ньютона

Пусть выполняется неравенство

f(x0)f00(x0) > 0 (4)

Теорема. Если

f(a) f(b) < 0

причем f0(x) f00(x) отличны от 0 и сохраняют определенные знаки на [a; b], то при любом начальном приближении x0 2 [a; b], удовлетворяющем неравенству (4) последовательность x1; x2; . . . ; xn получаемая по формуле (3) сходится к единственному корню у-ния (1).

Док-во. Положим для определенности

8

f(a) < 0

>

>

>

<f(b) > 0

на [a; b]

>f0(x) > 0

>

>

:f00(x) > 0

Остальные случаи доказываются аналогично. Из неравенства (4) имеем, что

f(x0) > 0 и x0 >

Методом математической индукции докажем, что все приближения

xn > n = 0; 1; 2; :::

следовательно

f(xn) > 0

Предположим, что xn > . Положим

= xn + ( xn)

По формуле Тейлора

0 = f( ) = f(xn) + f0(xn)( xn) + 12 f00(cn)( xn)2 (5)

где < cn < xn

Так как f00(x) > 0, то

12 f00(cn)( xn)2 > 0

откуда

f(xn) + f0(xn)( xn) < 0

откуда

< xn f0(xn) = xn+1 f (xn)

что и требовалось доказать.

Из формулы (3), учитывая знаки f(xn) и f0(xn) получим, что

xn+1 < xn

т. е. последовательность x0; x1; . . . ; xn ограниченная и монотонно-убывающая, значит существует предел

= lim xn

n!1

Переходя к пределу в равенстве (3) получим

= f( )

f0( )

т.е. f( ) = 0. Т.к. на интервале [a; b] у-ние (1) имеет единственный корень, то

=

13

4.3Оценка приближения

Получичим формулу для оценки точности приближения xn по методу Ньютона. Примененяя формулу Тейлора получим

f(xn) = f(xn 1 + (xn xn 1)) = f(xn 1) + f0(xn 1)(xn xn 1) + 12 f00( n 1)(xn xn 1)

где

n 1 2 (xn 1; xn)

В силу определения приближения xn (смотри формулу 3), имеем, что f(xn 1) + f0(xn 1) (xn xn 1) = 0

Из (6) получим, что

jf(xn)j = 12 jf00( n 1)(xn xn 1)2j 6 12 m2(xn xn 1)2

где m2 наибольшее приближение значения модуля второй производной f00(x) на [a; b]. Общая формула для оценки точности любого метода имеет вид

j xnj 6 jf(xn)j m1

где m1 - наименьшее значение модуля 1-ой производной fn(x) на [a; b]. Поэтому получим

j xnj 6 m2 (xn xn 1)2 (7)

2m1

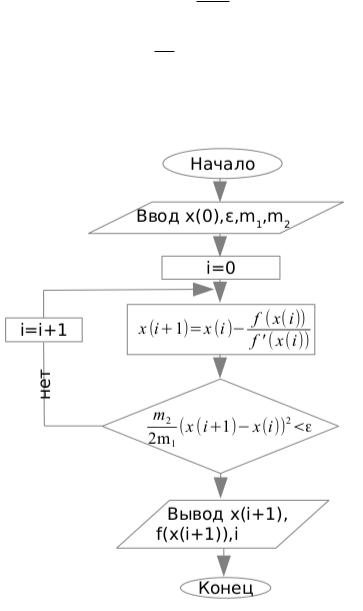
4.4Блок-схема алгоритма метода Ньютона

Входные параметры: x0; "; m1; m2 Выходные параметры: = x(i + 1); f( )

14