Часть V

Интерполирование (интерполяция ф-ий)

12 Постановка задачи интерполирования

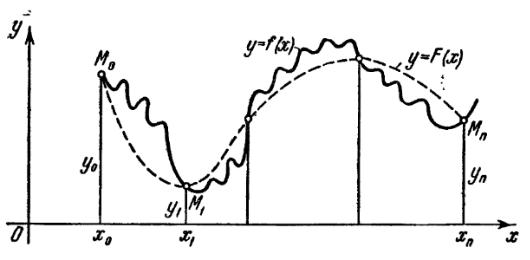
Задача интерполирования заключается в следующем: на отрезке [a; b] заданы n + 1 точек: x0; x1; :::; xnточек - узлы интерполяции. И заданы значения ф-ии

f(xn) = yn n = 0; 1; 2; ::: (1)

Требуется построить интерполирующую ф-ю F (x), принадлежащую некоторому классу функций и принимающую в узлах интерполяции те же значения, что и f(x). То есть

F (x0) = y0; F (x1) = y1; :::; F (xn) = yn (2)

В такой общей постановке задача может иметь бесчисленное множество решений.

Задача становится однозначной, если вместо произвольной F (x) искать полином Pn(x), степени не выше n, удовлетворяющий условиям (2). То есть, такой, что

Pn(x0) = y0; Pn(x1) = y1; :::; Pn(xn) = yn

Полученную интерполяционную формулу y = F (x) обычно используют для приближенного вычисления значений ф-и f(x) для значений аргумента x, отличных от узлов интерполяции. Такая операция называется интерполированием ф-и f(x).

13 Конечные разности

Пусть y = f(x) - заданная ф-я. Обозначим x = h - фиксированная величина приращения аргумента (шаг). Тогда выражение

y = f(x) = f(x + x) f(x) (1)

называется первой конечной разностью ф-и y. Аналогично определяются конечные разности старших порядков

ny = ( n 1y) (10)

необновляемое представление. Разность второго порядка равна

2y = ( y) = [f(x+ x) f(x)] = [f(x+2 x) f(x+ x)] [f(x+ x) f(x)] = f(x+2 x) 2f(x+ x)+f(x)

42

Символ можно рассматривать как оператор, ставящий в соответствие ф-и y = f(x) ф-ю y = f(x +x) f(x)

Оператор имеет следующие свойства:

1.(u + v) = u + v

2.(cu) = c u

3.m( ny) = m+ny, m и n - целые неотрицательные числа. По определению 0y = y

13.1Выражение ф-и f(x + n x) через конечные разности

Из формулы (1) имеем

f(x + x) = f(x) + f(x)

отсюда рассматривая как символический множитель, получим f(x + x) = (1 + )f(x) (2)

Применим формулу (2) для определения f(x + 2 x). По формуле (1) f(x + 2 x) f(x + x) = f(x + x)

отсюда

f(x + 2 x) = f(x + x) + f(x + x) = (1 + )f(x + x)

На основании формулы (2) получим

f(x + 2 x) = (1 + )2f(x)

Последовательно применяя соотношение (2) n раз получим

f(x + n x) = (1 + )nf(x) (3)

Воспользовавшись формулой бинома Ньютона окончательно получим

n

f(x + n x) = P Cnm mf(x) (4)

m=o

13.2Выражение конечной разности nf(x) через значение ф-и f(x + k x)

= (1 + ) 1 (5)

Применяя формулу бинома Ньютона, получим

n

nf(x) = [(1 + ) 1]nf(x) = P Cnk( 1)k(1 + )n kf(x)

k=o

Из последнего выражения на основании формулы (3) получим

n

nf(x) = P Cnk( 1)kf(x + (n k) x)

k=o

43