y = 0y2

1

y1

By

C

B

nC

@

:::

A

0

10y2

1

1

0

:::

0

B

p1

p2

p3

:::

pn

CB

y1

C

(P

E)

=

B

0

1

:::

0

y3

C

= 0

y

0

0

0

:::

CBy

B

:::

:::

:::

:::

:::

CB

nC

B

CB

:::C

Перемножая матрицы получим:

@

A@

A

8y11 y2

= 0

+ p3y3 + ::: + pnyn = 0

>

(p

)y1

+ p2y2

>y

2

y

3

= 0

(1)

>

>

>

>

>yn 1

yn = 0

<:::

>

>

>

>

>

Система

(1)

однородная т.е.

бесконечное множество решений.

:

С точностью до коэффициента пропорциональности ее решения могут быть найдены так: Положим yn = 1, получим

	8yn 2				= 2
			yn	1	=
	>
	>
	<
	>:::
	>y1 = n 1
	>
	>
Следовательно, собственный вектор	матрицы P равен
	:					1
					n 1
				0 n 2
	y = B					C
				B		C
				B	:::	C
					1
				B		C
				@		A

Обозначим x - собственный вектор матрицы A, соотвествующий данному , тогда x = Mn 1Mn 2:::M2M1y

10.2Метод вращений

10.2.1Трехдиагональная матрица

Матрица вида

0c1		a2	b2	:::	0		0	1
B	a1	b1	0	:::	0		0	C
B	0	c1	a3	:::	0		0	C
	0	0	0	:::	a	b
B		:::	:::	:::	n 1		n 1C		(1)
B:::					:::		:::	C
B								C
B								C
@								A

00 0 ::: cn 1 an

Найдем характеристический полином матрицы (1). Пусть Dk( ) укороченный полином матрицы

0c1		a2	b2	:::	0		0		1
B	a1	b1	0	:::	0		0		C
B	0	c1	a3	:::	0		0		C
	0	0	0	:::	a	b
B		:::	:::	:::	k 1		k 1C
Ak = B:::					:::		:::		C
B	0	0	0	:::	c		a	k	C
B					k 1				C
@									A

35

Тогда

c1

a2

b1

b2

:::

0

0

a1

0

:::

0

0

Dk( ) =

Ak

E

=

0

c

a

:::

0

0

j

j

2

3

0

0

0

:::

a

k 1

b

k 1

:::

:::

:::

:::

:::

:::

0

0

0

:::

c

a

k

k 1

Разлагая этот определитель по элементам

последнего столбца получим при k > 3

D ( ) = (a

)D ( )

b

:::

:::

:::

:::

::: = (a

)D

( )

b c

D ( ) (2)

a1

b1

:::

0

0

k

k

k 1

k 1

0

0

:::

a

b

k 2

k

k 1

k 1 k 1

k 2

k 2

0

0

:::

:::

ck 1

Данная формула верна и при k = 2, если положить, что

D0 = 1 и D1( ) = a1

Из формулы (2) следует, что

D2( ) = (a2 )D1( ) b1c1D0

Полагая в формуле (2) последовательно k = 2; 3; :::; n получим D2( ); D3( ); :::; Dn( ) Здесь Dn( ) - характеристический полином данной трехдиагональной матрицы A

10.2.2Ортогональные матрицы

Определение. Вещественная матрица называется ортогональной, если сумма квадратов элементов каждого столбца равна 1, а суммы произведений соотвествующих элементов из двух различных столбцов равны 0. Такое же свойство выполняется и для строк. Ортогональность матрицы может быть охарактеризована следующим матричным равенством A0A = E, A0- транспонированная матрица.

Свойства ортогональной матрицы:

1.единичная матрица ортогональна;

2.если матрица A ортогональна, то A0 = A 1;

3.если матрица A ортогональна, то A0 - тоже ортогональна;

4.произведение двух ортогональных матриц есть ортогональная матрица;

5.определитель ортогональной матрицы равен 1.

A0A = E, следовательно

jA0Aj = jEj = 1

С другой стороны

jA0Aj = jA0jjAj = jAj2 = 1

36

10.2.3Преобразование симметричной матрицы к трехдиагональному виду посредством вращений

Вращением называется преобразование координат с элементарной матрицой вращения

1

:::

:::

:::

:::

:::

:::

:::

:::

:::

0::: ::: ::: :::

:::

:::

:::

:::

:::

:::1

B

:::

1

:::

:::

:::

:::

:::

C

T

=

:::

:::

:::

(1)

B

:::

:::

c

0

:::

:::

s

:::

C

B:::

:::C

B

C

B:::

:::

:::

0

1

:::

:::

:::

:::

:::C

B

C

ij

B:::

:::

:::

:::

:::

:::

:::

:::

:::

:::C

B

C

B::: ::: ::: :::

:::

:::

1

0

:::

:::C

B

C

B:::

:::

:::

s

:::

:::

0

c

:::

:::C

B

:::

:::

:::

:::

:::

C

B::: ::: ::: :::

:::C

@

A

B:::

:::

:::

:::

:::

:::

:::

:::

:::

1 C

где c2 + s2 = 1

Геометрически вращение может быть интерпретировано как поворот базисных векторов eiи ej на некоторый угол в плоскости, в которой расположены эти векторы eiи ej

Покажем что любую симметричную матрицу можно привести к трехдиагональной форме посредством цепочки вращений с матрицами вида Tij.

Пусть A - симметричная матрица.

B = ATij C = Tij0 ATij = TijB

Tij0 - транспонированная матрица. Все столбцы матрицы B совпадают со столбцами матрицы A за исключением i j столбцов, которые получаются из соотвествующих столбцов матрицы A по формулам

Bi = cAi + sAjBj = sAi + cAj (2)

В свою очередь строки матрицы C совпадают со строками матрицы B, за исключением i j строк, которые получаются из соотвествующих строк матрицы B по таким же формулам

Ci = cBi + sBjCj = sBi + cBj

Пусть 1 < i < j. Коэффициенты s,c можно выбрать так, чтобы элемент

ci 1;j = bi 1;j = sai 1;i + cai 1;j = 0

То есть достаточно взять

s = ai 1;j

cai 1;i

Следовательно

s=	p	ai 1:j	, c=	p	ai 1:i
		ai2 1;i+ai2 1;j			ai2 1;i+ai2 1;j

Выбор знака в знаменателе безразличен. Весь процесс приведения симметричной матрице к трехдиагональной выглядит так:

1.за счет преобразований T23; T24; :::; T2nаннулируются по очереди элементы первой строки начиная с 3- его;

2.затем за счет преобразований T34; T35; :::; T3n аннулируются по очереди элементы второй строки начиная с 4-его при этом элементы первой строки больше меняться не будут;

3.далее за счет T45; T46; :::; T4n аннулируются по очереди элементы третьей строки начиная с 5-его и т.д.

После построения трехдиагональной матрицы (1) подобной исходной матрице A собственные значения могут быть найдены путем построения характеристического полинома Dn( ) по рекурентым формулам 2 (см. Трехдиагональная матрица).

37

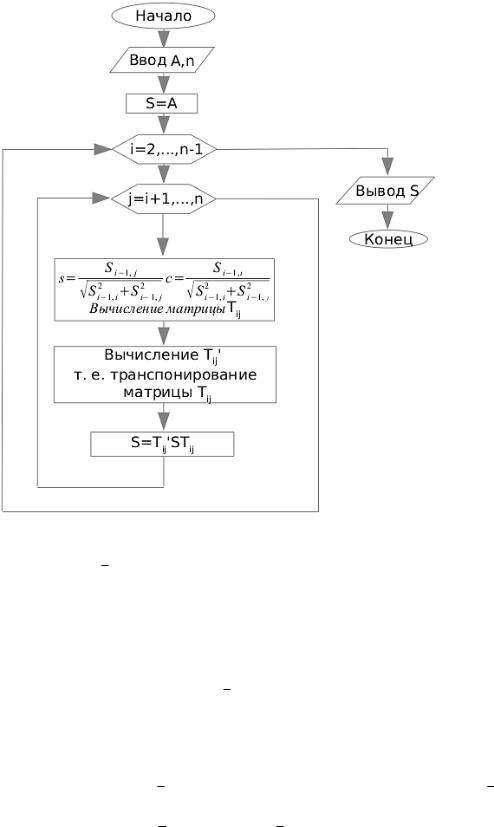
10.2.4Блок-схема алгоритма построения трехдиагональной матрицы

Входные параметры: n - порядок матрицы, A - исходная симметричная матрица Выходные параметры: S - трехдиагональная матрица

10.2.5Вычисление собственных векторов трехдиагональной матрицы и исходной матрицы

Вычисление собственных векторов y трехдиагональной матрицы (1) может быть осуществлено путем решения системы линейных у-ний.

8c1y1 + (a2				i)y2	+ b2y3 = 0
(a1	i)y1		+ b1y2		= 0
>					(4)

>

>

<

>:::

>

>

:cn 1yn 1 + (an i)yn = 0

где y1; y2; :::; yn - координаты собственного вектора yi, соотвествующего i Рекомендуется задать первую координату y1

Для перехода от собственных векторов трехдиагональной матрицы (1) к собственным векторам исходной матрицы A нужно использовать соотношение

C = Tn0 1;n:::T230 AT23:::Tn 1;n (5)

Из (5) следует, что собственный вектор x матрицы A соотвествующий собственному вектору y матрицы C равняется

x = T 23T 24:::T n 1;ny

38