6Решение систем линейных уравнений
Способы решения систем линейных уравнений в основном разделяются на две группы:
1.Точные методы. Представляют собой конечные алгоритмы для вычисления корней системы (правило Краммера, метод Гаусса, метод Гаусса-Жордана и д.р.)
2.Итерационные методы. Позволяющие получить корни системы с заданной точностью путем сходящихся бесконечных последовательностей (метод Якоби, метод Зейделя и д.р.)
7Метод Гаусса
Процесс решения системы уравнений по этому методу сводится к построению эквивалентной системы, имеющей треугольную матрицу (Прямой ход) с последующим нахождением решения (Обратный ход) Отличие определителя системы от нуля это необходимое и достаточное условие существования единственного решения системы.
В случае равенства нулю определителя система либо не имеет решений, либо имеет их бесчисленное множество.
Пусть дана система уравнений:
8
>a11x1
>
>
<a21x1
>. . . :
>
>
:an1x1
+ a12x2 + . . . + a1nxn = a1;n+1
+ a22x2 + . . . + a2nxn = a2;n+1
(1)
+ an2x2 + . . . + annxn = an;n+1
Ведущим элементом на каждой итерации с номером (k) назовем элемент akk 6= 0, а строку, содержащую этот элемент ведущей строкой.
7.1Прямой ход
Допустим, что a11 6= 0. Разделим коэффициенты первого у-ния системы (1) (включая и правую часть) на коэффициент a11, который будем называть ведущим элементом первого шага
ea1j = a1j j = 2; 3; ::n + 1
a11
Получим новое у-ние
x1 + ea12x2 + . . . + ea1nxn = ea1;n+1 (2)
Теперь вычтем из каждого i-отого у-ния системы (1) у-ние (2), умноженное соотвественно на коэффициент ai1. Получим новую эквивалентную систему уравнений.
>
8a22(1)x2 |
+ a23(1)x3 |
+ . . . + a2(1)n xn = a2(1);n+1 |
|
|||
x1 |
+ a12x2 |
+ . . . + a1nxn |
= a1;n+1 |
(3) |
||
|
e |
|
|
e |
e |
|
>
>
<
>. . . :
>
>
:a(1)n2 x2 + . . . + a(1)nnxn = a(1)n;n+1
где
a1j = a1j e a11
a(1)ij = aij aij ea1j i = 2; 3; :::; n j = 2; ::; n + 1
Разделим далее коэффициенты второго у-ния в система (3) на ведущий элемент a(1)22 , который будем считать отличным от 0. Получим у-ние
x2 + ea23x3 + ea24x4 + . . . + ea2nxn = ea2;n+1 (4)
18
Теперь вычтем из каждого i-отого у-ния системы i = 3; 4; ::; n (3) у-ние (4) умноженное на a(1)i2 получим:
8x2 |
+ a23x3 |
+ . . . + a2nxn |
= a2;n+1 |
|
||||||||||||
|
x1 |
+ a12x2 |
+ . . . + a1nxn |
= a1;n+1 |
|
|||||||||||
>a |
33 |
x |
3 |
+ |
. . . |
+ a |
3n |
x |
n |
= a |
3;n+1 |
(5) |
||||
> |
|
|
|
|
|
|
|
|||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
e |
|
|
|
|
|
e |
|
|
e |
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
||||
< |
|
|
|
|
e |
|
|
|
|
|
e |
|
|
e |
|
|
> |
|
(2) |
|
|
|
|
|
(2) |
|
(2) |
|
|||||
>
>. . . :
>
>
>
> (2) (2) (2) (1)
:an3 x3 + an4 x4 + . . . + annxn = an;n+1
Продолжая этот процесс на n-ом шаге получим систему уравнений.
8x2 |
+ a23x3 |
+ . . . + a2nxn = a2;n+1 |
|
|||||||||
> |
x1 |
+ a12x2 |
+ . . . + a1nxn = a1;n+1 |
|
||||||||
|
|
|
e |
|
|
|
|
|
e |
e |
|
|
>x |
3 |
+ |
. . . |
+ a |
3n |
x |
n |
= a |
3;n+1 |
(6) |
||
> |
|
|
|
|
|
|
|
|||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
e |
|
|
|
|
|
e |
e |
|
> |
|
|
|
|
|
|
|
|
|
|||
< |
|
|
|
|
|
e |
|
|
e |
|
||
|
|
|
|
|
|
|
|
|
||||
>
>. . . :
>
>
>
>
:xn = ean;n+1
Коэффициенты входящие в (1), (3), (5) и (6) определяются по следующим формулам
a(0)ij = aij i = 1; 2; :::; n j = 1; 2; :::; n + 1 (7)
на k-ом шаге
8
a(k 1)
<a = kj
ekj a(kkk 1)
:a(ijk) = a(ijk 1) a(ijk 1) eakj
k = 1; 2; :::; n j = k; k + 1; :::; n; n + 1
(8)
k = 1; :::; n 1 i = k + 1; :::; n j = k; k + 1; :::; n; n + 1
Необходимым и достаточным условием приведения матрицы к треугольному виду является отличие от нуля всех ведущих элементов
akk 6= 0 k = 1; 2; :::; n
Наибольшая точность достигается тогда, когда ведущий элемент строки имеет наибольшее значение, поэтому строку с нулевым или малым ведущим элементом надо заменить на ту из стоящих под ней строк, в которой в том же столбце стоит элемент, имеющий наибольшее значение.
7.2Обратный ход
В процессе обратного хода неизвестные определяются по формулам
8xn |
= a n;n |
|
|
n |
a |
|
x |
j = n 1; :::; 1 (9) |
|
< |
x |
= a |
+1 |
|
|
|
|
|
|
i |
ei;n+1 |
|
j=i+1 |
ij j |
|||||
: |
|
e |
|
|
P |
e |
|
|
|
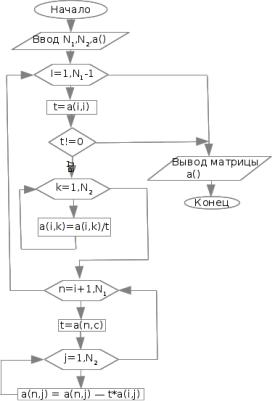
7.3Процедура приведения матрицы к треугольному виду
Входные данные N1 число строк, N2 число столбцов, a() - массив коэффициентов системы (включая правую часть)
Выходные данные a() - массив коэффициентов треугольной матрицы
19
7.4Обращение матриц методом Гаусса (Вычисление обратной матрицы методом Гаусса)
Пусть задана невырожденная матрицы
A = (aij) i; j = 1; 2; :::; n (1)
Для нахождения ее обратной матрицы
A 1 = (xij) (2)
используем соотношение
AA 1 = E
где Е единичная матрица (3). Перемножая матрицы получим n систем уравнений с n2неизвестными xij
n
P
aikxkj = ij i; j = 1; :::; n (4)
k=1
где
(
ij =
1 i = j
0 i 6= j
Полученные n систем уравнений (4) имеют одну и ту же матрицу A и различные правые части. Эти системы одновременно можно решить методом Гаусса.
Пример. Дана матрица
A = |
2 |
1 |
4 |
5 |
Найти обратную матрицу A 1
20