Часть I

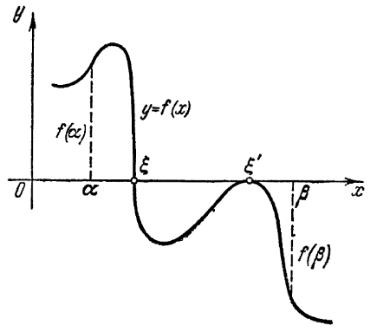
Численные методы решения нелинейных уравнений

f(x) = 0 (1)

f(x) определена и непрерывна на некотором конечном/бесконечном интервале. Всякое значение , такое, что

f( ) = 0

называется корнем у-ния (1) или нулем ф-и f(x).

Полагаем, что (1) имеет лишь изолированные корни т. е. для каждого корня уравнения (1) существует окрестность не содержащая других корней этого уравнения. Приближенное нахождение действительных изолированных корней обычно состоит из двух этапов:

1.отделение корней. Определение возможно меньших интервалов [a; b] в которых содержится лишь один корень уравнения (1);

2.уточнение приближенных корней.

1Нахождение корней методом половиного деления

Пусть ф-я f(x) определена на интервале [a; b]. Для отделения корней аналитическим методом используют следующую теорему.

Первая теорема Больцано-Коши: Если непрерывная ф-я f(x) принимает значения разных знаков на концах отрезка [a; b], то есть

f(a)f(b) < 0

то внутри этого отрезка содержится по меньшей мере один корень уравнения

f(x) = 0

т. е. найдется хотя бы одно число , такое, что

f( ) = 0

4

Док-во. Пусть дано у-ние

f(x) = 0 (1)

где ф-я f(x) непрерывна на [a; b]. Для определенности

(

f(a) < 0 f(b) > 0

Разделим интервал [a; b] пополам точкой a+2 b . Если

f(a+2 b ) = 0

то

=a+2 b

является корнем у-ния (1) и теорема доказана. Пусть

f(a+2 b ) 6= 0

тогда на концах одного из интервалов [a; a+2 b ] или [a+2 b ; b] функция будет принимать значения разных знаков. Причем отрицательное значение на левом, положительно на правом. Обозначим этот интервал как [a1; b1], причем

(

f(a1) < 0 f(b1) > 0

Разделим пополам интервал [a1; b1] и снова отбросим случай, когдаf(a+2 b ) = 0. Обозначим через [a2; b2] ту половину интервала [a1; b1] для которой

(

f(a2) < 0 f(b2) > 0

Продолжим этот процесс построения интервалов. После конечного числа шагов получим такую, что f( ) = 0, либо получим бесконечно последовательность вложенных друг в друга интервалов, таких что

(

f(an) < 0 (2) f(bn) > 0

bn an = b2na (3)

Так как левые концы интервалов образуют монотонно-неубывающую ограниченную последовательность, а правые монотонно-невозрастающую ограниченную последовательность, то эти последовательности сходятся и в силу равенства (3) у них существует общий предел:

	lim (b		n	a	) = lim		b a	= 0
							2n
	n	!1		n	n	!1

nlim (bn an) = nlim bn nlim an = 0
!1	!1	!1

= lim bn = lim an

n!1 n!1

Переходя к пределу в неравенствах (2) и используя при этом непрерывность ф-и получим:

f( ) = lim f(an) = f( lim an) 6 0

n!1 n!1

f( ) = lim f(bn) > 0

n!1

следовательно

f( ) = 0

Теорема 1 используется не только для отделения корней. Ее док-во дает метод приближенного вычисления корней метод половинного деления. Погрешность метода определяется неравенством

0 6 an 6 21n (b a)

5