следовательно
jx j 6 jf(x)j
m1
Теорема Лагранжа. Пусть функция f(x) определена и непрерывна в замкнутом интервале [a; b] и существует конечная производная f0(x) покрайней мере в открытом интервале (a; b), тогда между a и b найдется точка c a 6 c 6 b, такая что для нее выполняется равенство
f(b) f(a) = f0(c) b a
3Метод итерации
f(x) = 0 (1)
непрерывная ф-я.
Заменим у-ние (1) равносильным у-нием
x = '(x) (2)
Выберем каким-либо способом грубо приближенное значение корня x0 и подставим в правую часть (2), получим
x1 = '(x0) (3)
Подставим в правую часть (3), вместо x0 x1, получим
x2 = '(x1)
Повторяя этот процесс получим
xn = '(xn 1) (4)
Если эта последовательность сходящаяся, то есть существует предел
= lim xn
n!1
то переходя к пределу в равенстве (4) и считая, что '(x) непрерывная ф-я, получим
lim xn = '( lim xn 1)
n!1 n!1
или
= '( ) (5)
Следовательно корень у-ния (2), а следовательно и у-ния (1) и он может быть вычислен по у-нию (4) с любой степенью точности.
3.1Геометрическая модель
Отправляясь от некоторой точки A0 с координатами (x0; f(x0)) строим ломаную линию A0; B1; A1; B2; A2; . . .
звенья которой паралелльны осям Ox и Oy. Вершины A1; A2; A3; ::: лежат на кривой
y = '(x)
а B1; B2; B3 лежат на прямой
y = x
Общие абсциссы точек A1 B1; A2 B2; ::: представляют собой последовательные приближения x1; x2; ::: корня
.
7
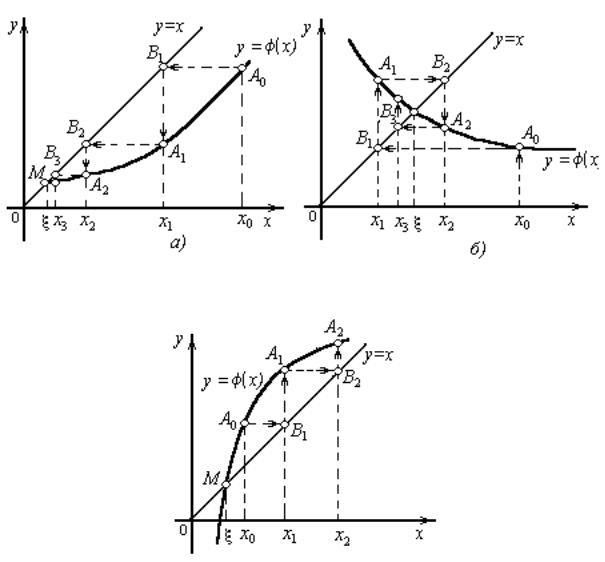
Но процесс последовательного приближения сходится не при любой функции '(x) (случай, где j'0(x)j > 1).
3.2Условие сходимости итерационного процесса
Теорема. Пусть ф-я '(x) определена и дифференцируемая на отрезке [a; b]. Причем все ее значения принадлежат этому отрезку [a; b]. Тогда если существует правильная дробь q, такая, что
j'0(x)j 6 q < 1 (6)
при a < x < b, то
1.Процесс итерации xn = '(xn 1) n = 1; 2; ::: сходится независимо от начального значенияОценка погрешности приближенного корня уравнения. x0, принадлежащего [a; b]
2.Предельное значение = lim xn является единственным корнем у-ния x = '(x) (8) на отрезке [a; b]
n!1
Док-во. Рассмотрим два последовательных приближения
xn = '(xn 1) xn+1 = '(xn)
Вычитая из второго первое получим
xn+1 xn = '(xn) '(xn 1)
8
Применив теорему Лагранжа, получим
xn+1 xn = (xn xn 1)'0(xn) xn 2 (xn 1; xn)
jxn 1 xnj 6 qjxn xn 1j (9)
Отсюда при n = 1; 2; 3. . . получим |
x2j |
6 qjx2 |
x1j |
|
|
8jx3 |
6 q2 x1 |
x0 |
|||
x2 |
x1 |
6 q x1 |
x0 |
j |
j (10) |
>j |
j |
j |
j |
||
> |
|
|
|
|
|
>
<
>:::
>
>
:jxn+1 xnj 6 qnjx1 x0j
x0 + (x1 x0) + (x2 x1) + ::: + (xn+1 xn)+. . . (11)
Ряд, для которого последовательные приближения x1; x2; :::; xnявляются (n + 1)-ми частными суммами
xn = Sn+1
т.е.
x1 = S2 x2 = S3 и т.д.
В силу неравенств (10) члены ряда (11) по абсолюной величине меньше соотвествующих членов геометрической прогрессии со знаменателем q < 1, эта прогрессия сходится и мажорирует ряд (11), поэтому ряд (11) сходится, а поскольку его слагаемыми являются абсолютные величины, то ряд (11) сходится абсолютно.
lim Sn+1 = lim xn = 2 [a; b]
n!1 n!1
Переходя к пределу в равенстве (7) в силу непрерывности ф-и '(x) получим
= '(x)
то есть корень у-ния (1).
Покажем, что на [a; b] единственный корень. Допустим, что существует 6= , следовательно
= '( ) (13)
= '( ) '( ) = ( )'0(c) c 2 ( ; )
тогда
( )[1 '0(c)] = 0
но
1 '0(c) 6= 0
значит
= 0
и единственный корень.
Пример невыполнения условий теоремы
j'0(x)j > 1
9