Так как h =	b na	, то полагают, что	Ai	= (b a)Hi
	где
			Hi = 1	( 1)n i n q[n+1] dq i = 0; 1; :::; n
			n i!(n i)!		0 q i

постоянные величины, называемые коэффициентами Котеса. Теперь формула (1) принимает вид

bn

P

ydx = (b a) Hiyi (8)

ai=0

где h = b na yi = f(a + ih)

Для коэффициентов Котеса выполняются соотношения

n

P

1.Hi = 1

i=0

2. Hi = Hn i

21	Формула трапеций
Из формулы (7) при n = 1
		1		q(q 1)		1
		H0 =				dq = 2
				q
		0
		H1 =	1
				qdq = 1
						2
			0
Следовательно
		x1
		ydx = h (y0 + y1) (1)
		2
		x
		0
		h = x1 x0 = b a
формула трапеции для элементарного промежутка.
21.1	Формула погрешности
	x1	x0+h	ydx h2 [y(x0) + y(x0 + h)] = R(h)
	R =	ydx h2 (y0 + y1) =
	x	x
	0	0
Найдем первую и вторую производную от погрешности R от n.
	R0(h) = y(x0 + h) 21 [y(x0) + y(x0 + h)] h2 y0(x0 + h) = 21 [y(x0 + h) y(x0)] h2 y0(x0 + h)
	R00(h) = 21 y0(x0 + h) 21 y0(x0 + h) h2 y00(x0 + h) = h2 y00(x0 + h)
		R(0) = 0 R0(0) = 0

Отсюда, интегрируя по h и используя обобщенную теорему о среднем последовательно получаем

h

R00(t)dt = 21

h

ty00(x0

h

( 1) 1 2 (x0; x0 + h)

R0(h) = R0(0) +

+ t)dt = 21 y00( 1) tdt = h42 y00

0

0

0

Далее

R(h) = R(0) +

h

(t)dt =

41

h

( 1)dt = 41 y00( )

h

( ) 2 (x0; x0 + h)

R0

t2y00

t2dt = h123 y00

0

0

0

Следовательно

R =

h3

y00( ) 2 (x0; x0 + h) (2)

12

54

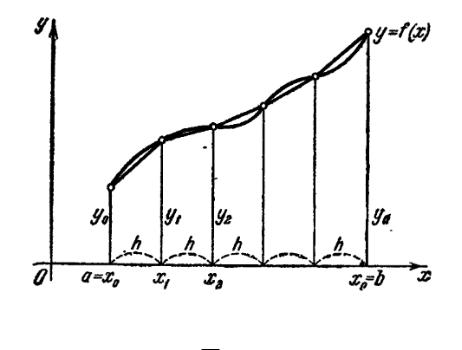
21.2Общая формула трапеций

Для вычисления интеграла

b

ydx

a

разделим промежуток [a; b] на n равных частей [x0; x1], [x1; x2], ... , [xn 1; xn] и к каждому из них применим формулу трапеций.

Введем обозначения

a = x0 b = xn h = b na yi = f(xi) i = 0; 1; 2; :::; n

тогда

b

ydx = h2 (y0 + y1) + h2 (y1 + y2) + ::: + h2 (yn 1 + yn) = h(y20 + y1 + ::: + yn 1 + y2n ) (3)
a
Погрешность формулы трапеции в силу выражения (2) будет равной
R = xnydx h2	n	(yi 1 yi) =	n	[ xi	ydx h2 (yi 1 + yi)] = h123 n				y00( i) i 2 (xi 1; xi) (4)
0	P		P	xi	1			P
x	i=1		i=1					i=1
Рассмотрим среднее арифметическое
					n
				= 1		y00( i) (5)
					iP
					n
					=1
Оно ограничено

m2 6 6 M2

наименьшим и наибольшим значением второй производной y00(x) на отрезке [a; b]. Так как y00(x) непрерывна на отрезке [a; b] то найдется такая точка , что

		= f00( )
Тогда из (4) и (5) следует, что
	nh3		(b a)h2		(b a)3
R =	12 y00	( ) =	12	y00( ) =	12h2	y00( )

Применение формулы трапеции приводит к погрешности того же порядка, что и применение формулы многоугольников.

55