Глава 4. Динамика вращательного движения.

§ 4.1. Кинетическая энергия вращающегося и катящегося тел

1. Найдем кинетическую энергию тела, вращающегося относительно неподвижной оси. Используем модель а.т.т. как сумму м.т. (рис.16). Все точки тела движутся по окружностям, траектория одной из них массой m_i, движущейся по окружности радиусом r_i со скоростью υ_i. указана на рисунке. Кинетическая энергия этой точки 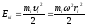. Найдем кинетическую энергию тела как сумму кинетических энергий образующих его точек: 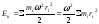. Полученный результат показывает, что кинетическая энергия вращающегося тела определяется двумя величинами: его угловой скоростью и еще одной индивидуальной характеристикой тела, зависящей от распределения его массы относительно оси вращения: 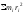. Ее называют моментом инерции тела относительно оси:

I =m_ir_i² (4.1.1)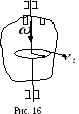

Формула кинетической энергии вращающегося тела имеет вид:

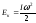(4.1.2)

2. В § 1.4 мы отмечали, что произвольное движение твердого тела можно представить как сумму двух движений: поступательного и вращательного. На практике часто встречается качение твердого тела – это вид плоского движения, т.е. такого движения, когда все точки тела перемещаются в параллельных плоскостях. Кинетическая энергия катящегося тела складывается из двух частей:

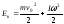(4.1.3)

Здесь v₀ - скорость поступательного движения центра инерции, I₀ – момент инерции тела относительно оси, проходящей через центр инерции тела перпендикулярно плоскостям перемещения его точек.

§ 4.2. Момент инерции

1. Из формул (4.1.2) и (4.1.3) следует, что момент инерции тела при вращательном движении является аналогом массы при его поступательном движении, а именно, служит мерой инертности тела, т.е. его способности сопротивляться изменению скорости: чем больше инертность тела, тем труднее изменить его скорость. Из определения момента инерции (см. формулу 4.1.1) следует, что инертность тела при вращении зависит от распределения его массы относительно оси вращения. Это означает, что одно и то же тело относительно разных осей вращения имеет разные моменты инерции. Это нам хорошо известно из опыта: чем дальше вращающаяся масса от оси вращения, тем труднее ускорить или замедлить ее вращение. Момент инерции, как и масса, скалярная величина, его единица измерения в СИ обозначается кг^.м².

Для сплошного однородного тела, рассматриваемого как совокупность м.т., с точки зрения математики удобно суммирование свести к интегрированию. Пусть dm – масса физически малого элемента объема dV ¹, находящегося на расстоянии r от оси вращения, плотность вещества тела -  (кг/м³), тогда dm= dV , и момент инерции этого элемента массы dI = r²dm = r² dV . Формула для вычисления момента инерции сплошного тела примет вид:

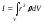(4.2.1)

Интегрирование проводят по всему объему тела, это обозначено ниже знака интеграла.

2. Приведем формулы моментов инерции некоторых тел, часто встречающихся в практике.

а) Обруч или тонкостенный цилиндр массой m и радиусом R , вращающийся относительно своей оси симметрии. Учитывая, что все элементы массы m находятся на одинаковом расстоянии от оси, получаем по формуле (4.1.1):

I =m_ir_i² = R²m_i = m R² (4.2.2)

б) Диск или сплошной цилиндр массой m и радиусом R , вращающийся относительно своей оси симметрии. Используем формулу (4.2.1), для этого диск разобьем на кольцевые слои. Один такой слой толщиной dr, высотой диска h и объемом dV=2rhdr показан на рис. 17. Момент инерции такого элементарного слоя в виде кольца dI= r² dV= r² 2rhdr=2hr³dr. Заметим, что в этом примере интегрирование по объему тела свелось к интегрированию по расстоянию r от оси до внешней поверхности цилиндра, так что 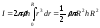. Учитывая, что объем цилиндра V=Sh=R²h, а его масса m=V, получили: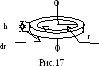

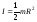(4.2.3)

Используя изложенный в этой главе материал, объясните, одновременно ли достигнут конца спуска два цилиндра одинаковых размеров, если один из них сплошной, а другой пустотелый, и они одновременно начали скатываться с вершины наклонной плоскости (вспомните лекционную демонстрацию).

в) Шар, вращающийся относительно своей оси (эту формулу нетрудно получить интегрированием, перейдя в сферическую систему координат):

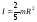(4.2.4)

г) Стержень длиной l, вращающийся относительно перпендикулярной к нему оси, проходящей через его середину (получите эту формулу самостоятельно):

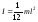(4.2.5)

д) Теорема Штейнера позволяет найти момент инерции тела относительно любой оси, если известен его момент инерции относительно параллельной оси, проходящей через центр инерции тела:

I=I₀+mb² (4.2.6)

Здесь I – момент инерции тела относительно рассматриваемой оси, I₀ - момент инерции этого же тела относительно оси, проходящей через центр инерции и параллельной рассматриваемой, b – расстояние между этими осями. Обратите внимание, что момент инерции тела относительно любых параллельных осей наименьший в случае, когда ось проходит через центр инерции. Самостоятельно получите формулу для момента инерции стержня, если ось вращения проходит через его конец и перпендикулярна стержню.