
- •Предмет физики
- •Структура физического познания.
- •Пространственно-временная область изучаемых физикой объектов
- •Физические теории
- •Раздел 1. Физические основы механики.
- •Глава 1. Кинематика.
- •§1.1. Система отсчета. Инерциальные системы отсчета. Принцип относительности.
- •§1.2. Кинематика материальной точки.
- •§1.3. Равномерное и равнопеременное движения.
- •§ 1.4. Кинематика вращательного движения.
- •§ 1.5. Краткие итоги главы 1.
- •Глава 2. Динамика материальной точки.
- •§ 2.1 .Задача динамики. Состояние материальной точки. Динамические характеристики движения.
- •§ 2.2. Законы Ньютона. Второй закон как уравнение движения.
- •§ 2.3. Силы в механике.
- •§ 2.4. Работа силы. Мощность.
- •§ 2.4. Механическая энергия.
- •§ 2.5. Краткие итоги главы 2
- •Глава 3.Законы сохранения в механике.
- •§ 3.1.Фундаментальный характер законов сохранения
- •§ 3.2. Закон сохранения импульса.
- •§ 3.3. Закон сохранения механической энергии
- •§ 3.4. Столкновения тел
- •Глава 4. Динамика вращательного движения.
- •§ 4.1. Кинетическая энергия вращающегося и катящегося тел
- •§ 4.2. Момент инерции
- •§ 4.3. Работа и мощность при вращательном движении. Момент силы относительно оси
- •§ 4.4. Уравнение динамики вращательного движения.
- •§ 4.5. Закон сохранения момента импульса
- •§ 4.6. Краткие итоги главы 4
- •Раздел 2. Молекулярная физика и термодинамика
- •Глава 5. Кинетическая теория
- •§ 5.1. Тепловое движение
- •§ 5.2. Основное уравнение кинетической теории газа
- •§ 5.3. Уравнение Клапейрона – Менделеева
- •§ 5.4. Молекулярно-кинетический смысл абсолютной температуры. Средняя энергия теплового движения молекулы
- •§ 5.5. Распределение Максвелла молекул газа по скоростям
- •§ 5.6. Барометрическая формула. Распределение Больцмана.
- •§ 5.7. Среднее число столкновений и средняя длина свободного пробега молекул.
- •§ 5.8. Выводы из главы 5.
- •Глава 6. Термодинамика.
- •§ 6.1. Тепловые процессы
- •§ 6.2. Первое начало термодинамики.
- •§ 6.3 Изопроцессы.
- •§ 6.4. Тепловая и холодильная машины
- •§ 6.5. Цикл Карно
- •§ 6.6. Энтропия.
- •§ 6.7. Второе начало термодинамики.
- •§ 6.8. Основные выводы главы 6.
- •Раздел 3. Электромагнетизм
- •Глава 7. Электростатика
- •§7.1.Электрический заряд. Закон Кулона.
- •§7.2. Электрическое поле. Напряженность.
- •§ 7.3. Теорема Гаусса.
- •§ 7.4. Потенциал и работа электростатического поля.
- •§ 7.5. Связь напряженности и потенциала электростатического поля.
- •§ 7.6.Электростатическое поле в веществе.
- •§ 7.7. Электроемкость. Конденсатор.
- •§ 7.8. Энергия электрического поля.
- •Глава 8. Постоянный электрический ток.
- •§ 8.1. Электрический ток: сила тока, плотность тока
- •§ 8.2. Механизм электропроводности
- •§ 8.3. Законы постоянного тока.
- •§ 8.4. Работа и мощность тока
- •Глава 9. Магнитное поле тока
- •§ 9.1 Магнитное взаимодействие. Магнитное поле
- •§ 9.2. Закон Био-Савара-Лапласа
- •9.3. Вихревой характер магнитного поля.
- •§ 9.4. Действие магнитного поля на токи и движущиеся электрические заряды
- •§ 9.5. Магнитное поле в веществе
- •Глава 10. Явление электромагнитной индукции
- •§ 10.1. Основной закон электромагнитной индукции
- •§ 10.2. Самоиндукция и взаимная индукция
- •§ 10.3. Энергия магнитного поля
- •§ 10.4. Вихревое электрическое поле. Уравнения Максвелла
§1.3. Равномерное и равнопеременное движения.
1. Взаимосвязь трех кинематических характеристик: закона движения, скорости и ускорения, рассмотренная в предыдущем параграфе, позволяет найти по одной известной кинематической характеристики остальные две. В предыдущем параграфе мы рассмотрели, как, зная закон движения, найти скорость и ускорение м. т. в любой момент времени. В этом параграфе рассмотрим решение обратной задачи кинематики: найти скорость как функцию времени и получить закон движения, зная зависимость ускорения от времени. Проделаем это на примерах равномерного и равнопеременного движений. Убедимся в том, что известные из школы формулы можно легко вывести, а не запоминать.
2. Равномерным называется движение,
когда скорость не изменяется по величине,
следовательно, тангенциальное ускорение
a
=0. Учитывая, что a=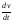 ,
получаем:
,
получаем:
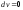 ,
т.е. υ=
,
т.е. υ=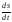 =const.
Находим первообразную (интегрируем) и
получаем формулу равномерного движения:
=const.
Находим первообразную (интегрируем) и
получаем формулу равномерного движения:
s=so+υt (1.3.1)
Здесь so –координата тела на траектории в начальный момент времени t=0. Если начало отсчета совместить с начальным положением тела, то so=0, и s = υt.
3. Равнопеременным называется
движение с постоянным ускорением
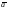 =const.
По аналогии с проделанным в предыдущем
п.1, проинтегрируем формулы (1.2.11) и
(1.2.6):
=const.
По аналогии с проделанным в предыдущем
п.1, проинтегрируем формулы (1.2.11) и
(1.2.6):
 (1.3.2)
(1.3.2)
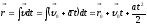 (1.3.3)
(1.3.3)
В этих
формулах
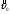 и
и
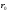 - начальная скорость и начальный
радиус-вектор м.т (при t=0).
- начальная скорость и начальный
радиус-вектор м.т (при t=0).
4. Примером равнопеременного движения
является свободное падение тела, при
этом тело движется с ускорением
свободного падения g=9,8
м/с2, направленным отвесно вниз
к земле. Рассчитаем траекторию свободного
падения тела, брошенного горизонтально
с некоторой высоты над поверхностью
земли. Тело движется в вертикальной
плоскости и имеет две степени свободы,
так что нарисуем две оси декартовых
координат, поместив начало отсчета в
точку старта тела. Ось x
направим горизонтально, ось y
направим вертикально вниз (рис.6).
Закон движения тела имеет вид (1.3.3),
причем, r0=0,
вектор начальной скорости
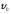 направлен по оси х. Запишем этот
закон в проекциях на оси координат:
направлен по оси х. Запишем этот
закон в проекциях на оси координат: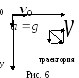
x=υ0t
y=gt2/2.
Мы получили
уравнение траектории (линии), заданное
параметрически. Выразим из первого
уравнения t, подставим
его во второе: у=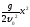 .
Итак, при свободном падении тело летит
по параболе. На практике такому движению
мешает сопротивление воздуха, так что
полученный нами результат приближенный.
.
Итак, при свободном падении тело летит
по параболе. На практике такому движению
мешает сопротивление воздуха, так что
полученный нами результат приближенный.
§ 1.4. Кинематика вращательного движения.
Абсолютно твердое тело (а.т.т.) - еще
одна модель механики. Она учитывает
размеры и форму тела, но пренебрегает
их изменением при движении, т.е.
деформациями. А.т.т. можно считать
системой материальных точек, взаимное
расположение которых не изменяется.
Любое движение а.т.т. можно представить
как сумму поступательного и вращательного
движений. При поступательном
движении все точки тела имеют
одинаковые скорости и одинаковые
ускорения в любой момент времени. При
вращательном движении траектории
всех точек тела – окружности, их
плоскости совпадают или параллельны
друг другу, а центры лежат на одной
прямой (ее называют ось вращения). На
рис. 7 представлены два положения
движущегося твердого тела, они
обозначенные числами 1 и 2. Траектория
движения некоторой точки А тела указана
пунктиром. Перемещение тела из положения
1 в положение 2 может быть осуществлено
разными способами. Две возможных
комбинации поступательного и вращательного
движений показаны промежуточными
положениями тела. Первый вариант:
сначала поступательное движение 11,
затем вращательное 11,
и опять поступательное 12.
Второй вариант: сначала поступательное
движение 12,
затем вращательное 22.
Можно рассмотреть еще множество разных
вариантов, но в любом из них угол поворота
тела будет
один и тот же, а вот скорость поступательного
движения может быть различной. 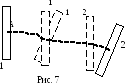
Из рассмотренного ясно, что поступательное движение тела сводится к движению точки. Освоив кинематику вращательного движения, мы сможем справиться с кинематикой произвольного движения тела.
2. На рис.8 показано а.т.т. произвольной
формы, вращающееся вокруг вертикальной
оси, закрепленной в неподвижных
подшипниках, изображенных скобочками.
Указаны траектории движения двух точек
тела. Радиусы и плоскости окружностей,
описываемых этими точками, различны,
а вот центральные углы, на которые
опираются дуги, описанные разными
точками при вращении тела, одинаковы.
Из этих рассуждений следует, что
вращающееся тело имеет всего одну
степень свободы: i
=1. Его положение в пространстве задает
одна координата - угол поворота тела
относительно некоторого положения,
выбранного за начало отсчета. Закон
вращательного движения выражает
уравнение 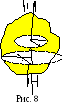
= (t) (1.4.1)
Разность
угловых координат в конечный t2
и начальный t1
моменты времени равна пути при
вращении, измеряемом углом
= 2
- 1.
Малые угловые перемещения (2)
можно считать векторами1,
будем их обозначать
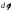 .
Этот вектор направлен вдоль оси в
соответствии с правилом правого винта,
т.е. указывает направление вращения
тела, и не имеет фиксированной точки
закрепления. Такой вектор называется
аксиальным (осевым) в отличие от полярных
векторов
.
Этот вектор направлен вдоль оси в
соответствии с правилом правого винта,
т.е. указывает направление вращения
тела, и не имеет фиксированной точки
закрепления. Такой вектор называется
аксиальным (осевым) в отличие от полярных
векторов
 ,
,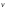 ,
,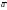 ,
рассмотренных нами в § 1.2.
,
рассмотренных нами в § 1.2.
Быстроту вращения характеризует угловая скорость .
Средняя угловая скорость
<>= /t (1.4.2)
Мгновенная угловая скорость
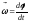 (1.4.3)
(1.4.3)
Быстроту изменения угловой скорости описывает угловое ускорение . Его среднее значение
<> = /t (1.4.4)
Мгновенное угловое ускорение
 (1.4.5)
(1.4.5)
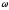 и
и
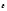 -
аксиальные векторы, направленные вдоль
оси, как и
-
аксиальные векторы, направленные вдоль
оси, как и
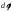 .
Направление вектора угловой скорости
определяет правило правого винта, а
направление вектора углового ускорения
зависит от знака изменения угловой
скорости: при ускоренном вращении
.
Направление вектора угловой скорости
определяет правило правого винта, а
направление вектора углового ускорения
зависит от знака изменения угловой
скорости: при ускоренном вращении
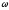 и
и
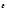 направлены вдоль оси в одну сторону,
при замедленном – в противоположные
стороны. В СИ угловая координата
измеряется в радианах (рад), угловая
скорость в рад/с, угловое ускорение в
рад/с2.
направлены вдоль оси в одну сторону,
при замедленном – в противоположные
стороны. В СИ угловая координата
измеряется в радианах (рад), угловая
скорость в рад/с, угловое ускорение в
рад/с2.
3. Найдем связь между линейными и угловыми
кинематическими характеристиками
точки вращающегося тела. На рис. 9
показана траектория некоторой точки
тела, отстоящей от оси вращения на
расстоянии R, ее
линейная скорость
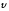 и
угловая скорость
и
угловая скорость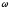 .
За промежуток времени t
тело повернулось на угол ,
а точка прошла путь s.
Очевидно, s=R.
Исходя из определений линейной и
угловой скоростей (формулы 1.2.8 и 1.4.3)
получаем:
.
За промежуток времени t
тело повернулось на угол ,
а точка прошла путь s.
Очевидно, s=R.
Исходя из определений линейной и
угловой скоростей (формулы 1.2.8 и 1.4.3)
получаем:
υ=R (1.4.6)
Используя формулы (1.2.13) и (1.2.15), получаем:
a = R (1.4.7)
an= 2R (1.4.8)
Обратите внимание, что нормальное ускорение всегда бывает у точек вращающегося тела, а тангенциальное только при неравномерном вращении.
