
- •Предмет физики
- •Структура физического познания.
- •Пространственно-временная область изучаемых физикой объектов
- •Физические теории
- •Раздел 1. Физические основы механики.
- •Глава 1. Кинематика.
- •§1.1. Система отсчета. Инерциальные системы отсчета. Принцип относительности.
- •§1.2. Кинематика материальной точки.
- •§1.3. Равномерное и равнопеременное движения.
- •§ 1.4. Кинематика вращательного движения.
- •§ 1.5. Краткие итоги главы 1.
- •Глава 2. Динамика материальной точки.
- •§ 2.1 .Задача динамики. Состояние материальной точки. Динамические характеристики движения.
- •§ 2.2. Законы Ньютона. Второй закон как уравнение движения.
- •§ 2.3. Силы в механике.
- •§ 2.4. Работа силы. Мощность.
- •§ 2.4. Механическая энергия.
- •§ 2.5. Краткие итоги главы 2
- •Глава 3.Законы сохранения в механике.
- •§ 3.1.Фундаментальный характер законов сохранения
- •§ 3.2. Закон сохранения импульса.
- •§ 3.3. Закон сохранения механической энергии
- •§ 3.4. Столкновения тел
- •Глава 4. Динамика вращательного движения.
- •§ 4.1. Кинетическая энергия вращающегося и катящегося тел
- •§ 4.2. Момент инерции
- •§ 4.3. Работа и мощность при вращательном движении. Момент силы относительно оси
- •§ 4.4. Уравнение динамики вращательного движения.
- •§ 4.5. Закон сохранения момента импульса
- •§ 4.6. Краткие итоги главы 4
- •Раздел 2. Молекулярная физика и термодинамика
- •Глава 5. Кинетическая теория
- •§ 5.1. Тепловое движение
- •§ 5.2. Основное уравнение кинетической теории газа
- •§ 5.3. Уравнение Клапейрона – Менделеева
- •§ 5.4. Молекулярно-кинетический смысл абсолютной температуры. Средняя энергия теплового движения молекулы
- •§ 5.5. Распределение Максвелла молекул газа по скоростям
- •§ 5.6. Барометрическая формула. Распределение Больцмана.
- •§ 5.7. Среднее число столкновений и средняя длина свободного пробега молекул.
- •§ 5.8. Выводы из главы 5.
- •Глава 6. Термодинамика.
- •§ 6.1. Тепловые процессы
- •§ 6.2. Первое начало термодинамики.
- •§ 6.3 Изопроцессы.
- •§ 6.4. Тепловая и холодильная машины
- •§ 6.5. Цикл Карно
- •§ 6.6. Энтропия.
- •§ 6.7. Второе начало термодинамики.
- •§ 6.8. Основные выводы главы 6.
- •Раздел 3. Электромагнетизм
- •Глава 7. Электростатика
- •§7.1.Электрический заряд. Закон Кулона.
- •§7.2. Электрическое поле. Напряженность.
- •§ 7.3. Теорема Гаусса.
- •§ 7.4. Потенциал и работа электростатического поля.
- •§ 7.5. Связь напряженности и потенциала электростатического поля.
- •§ 7.6.Электростатическое поле в веществе.
- •§ 7.7. Электроемкость. Конденсатор.
- •§ 7.8. Энергия электрического поля.
- •Глава 8. Постоянный электрический ток.
- •§ 8.1. Электрический ток: сила тока, плотность тока
- •§ 8.2. Механизм электропроводности
- •§ 8.3. Законы постоянного тока.
- •§ 8.4. Работа и мощность тока
- •Глава 9. Магнитное поле тока
- •§ 9.1 Магнитное взаимодействие. Магнитное поле
- •§ 9.2. Закон Био-Савара-Лапласа
- •9.3. Вихревой характер магнитного поля.
- •§ 9.4. Действие магнитного поля на токи и движущиеся электрические заряды
- •§ 9.5. Магнитное поле в веществе
- •Глава 10. Явление электромагнитной индукции
- •§ 10.1. Основной закон электромагнитной индукции
- •§ 10.2. Самоиндукция и взаимная индукция
- •§ 10.3. Энергия магнитного поля
- •§ 10.4. Вихревое электрическое поле. Уравнения Максвелла
§1.2. Кинематика материальной точки.
1.Задача кинематики – описание механического движения. Кинематические характеристики – закон движения (в быту мы его обычно называем расписанием), скорость и ускорение. Знание одной из них как функции времени позволяет найти остальные две, и мы этим постоянно пользуемся в своей жизни.
2. Для теоретического описания физических объектов используют их модели. Простейшая модель механики – материальная точка. Материальной точкой или частицей называют тело, размеры которого, форма, внутренняя структура и протекающие в нем процессы в данной задаче не влияют на его движение. Например, рассматривая орбитальное движение Земли вокруг Солнца, ее можно считать материальной точкой. В других задачах, например, при изучении процессов, происходящих в земной коре (землетрясение), модель материальной точки неприемлема. Следует помнить о том, что в классической механике частицы должны быть классическими телами, а не квантовыми. Столь маленькие с обыденной точки зрения объекты, как электроны, создающие изображение на экране кинескопа, вполне соответствуют модели материальной точки, тогда как такие же электроны при своем движении в атоме являются квантовыми объектами, и модель материальной точки к ним не применима.
3. Закон движения известен, если
известно положение тела в пространстве
в каждый момент времени. Этот закон
может быть задан таблицей, графиком,
уравнением (его называют кинематическим
уравнением движения). 
Положение материальной точки в
пространстве указывает радиус - вектор
 ,
проведенный из начала отсчета в точку,
где находится тело (рис. 2). При движении
этот вектор изменяется со временем t,
так что закон движения в векторной
форме выражает уравнение:
,
проведенный из начала отсчета в точку,
где находится тело (рис. 2). При движении
этот вектор изменяется со временем t,
так что закон движения в векторной
форме выражает уравнение:
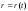 (1.2.1)1
(1.2.1)1
В декартовой системе координат этот же закон движения в координатной форме выражают три скалярных уравнения:
x=x(t)
y=y(t) (1.2.2)
z=z(t)
Согласие между законами движения в векторной (1.2.1) и в координатной (1.2.2) формах есть выражение принципа независимости движения: пространственное движение м.т. можно представить как сумму трех прямолинейных движений вдоль осей координат.
Линия, по которой движется тело, называется траекторией. Уравнение траектории задано законом движения. Закон движения в координатной форме (1.2.2) задает это уравнение в параметрической форме, где параметром является время t . Подчеркнем, что понятие траектории применимо только в классической физике, для квантовых частиц оно теряет смысл
Минимальное число параметров (координат), задающих положение тела, называется его числом степеней свободы – i . На рис 1 рассмотрено трехмерное движение м.т. ( i =3), движение по известной поверхности имеет две степени свободы и называется двухмерным, движение по известной траектории (например, поезда по рельсам или автомобиля по шоссе) называется одномерным. При одномерном движении закон движения превращается в одно скалярное уравнение:
s = s(t) (1.2.3)
В приведенном уравнении s – координата точки траектории. Если s=0 – тело находится в начале отсчета, если s>0 или s <0 – тело смещено на расстояние s, измеренное вдоль траектории от начала отсчета соответственно в положительном или в отрицательном направлениях.
4. Следующая кинематическая характеристика
движения – скорость – характеризует
быстроту изменения положения тела в
пространстве. Пусть положение тела в
момент времени t1
указывал радиус – вектор
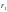 ,
а в момент времени t2
радиус - вектор
,
а в момент времени t2
радиус - вектор
 .
Вектор перемещения (рис.3)
.
Вектор перемещения (рис.3)
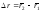 (.1.2.4)
(.1.2.4)
Путь s
– расстояние, пройденное телом по
траектории. При движении по прямолинейной
траектории в одном направлении модуль
вектора веремещения и пройденный путь
равны друг другу: 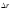 =
s.
Заметим, что по определению, путь –
положительная арифметическая величина.
Если направление движения тела изменяется
на противоположное, то путь равен сумме
длин, измеренных вдоль траектории, при
любом направлении движения. Например,
когда мы ушли из дома, а потом вернулись
домой, то вектор перемещения равен
нулю, а вот пройденный путь, и об этом
свидетельствует наша усталость, совсем
не равен нулю. В случае движения по
криволинейной траектории, а также при
изменении направления движения по
траектории любой формы
=
s.
Заметим, что по определению, путь –
положительная арифметическая величина.
Если направление движения тела изменяется
на противоположное, то путь равен сумме
длин, измеренных вдоль траектории, при
любом направлении движения. Например,
когда мы ушли из дома, а потом вернулись
домой, то вектор перемещения равен
нулю, а вот пройденный путь, и об этом
свидетельствует наша усталость, совсем
не равен нулю. В случае движения по
криволинейной траектории, а также при
изменении направления движения по
траектории любой формы
s.
s. 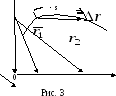
Вектор средней скорости за промежуток времени t = t2 – t1 равен:
< >=
>=
 (1.2.5)
(1.2.5)
Направление вектора средней скорости
совпадает с направдением вектора
перемещения. Из рис. 2 видно, что если
рассматриваемый участок пути разделить
на два одинаковых, то на каждом из них
векторы средних скоростей будут
различаться, так что < >
- довольно грубая характеристика
движения. Для получения более точной
характеристики надо рассматривать
маленькие участки траектории, которым
соответствуют маленькие промежутки
времени. Предел выражения (1.2.5) при
стремлении промежутка времени t
к нулю дает мгновенную скорость. В
математике такую операцию называют
нахождением производной, так что по
определению вектор мгновенной скорости
>
- довольно грубая характеристика
движения. Для получения более точной
характеристики надо рассматривать
маленькие участки траектории, которым
соответствуют маленькие промежутки
времени. Предел выражения (1.2.5) при
стремлении промежутка времени t
к нулю дает мгновенную скорость. В
математике такую операцию называют
нахождением производной, так что по
определению вектор мгновенной скорости
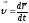 (1.2.6)
(1.2.6)
Направлен
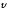 по касательной к траектории, так что
ему можно придать вид:
по касательной к траектории, так что
ему можно придать вид:
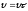 (1.2.7)
(1.2.7)
где υ –
модуль скорости,
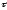 -
касательный орт, т.е. единичный вектор,
направленный по касательной к траектории.
-
касательный орт, т.е. единичный вектор,
направленный по касательной к траектории.
На практике зачастую интерес представляет только численное значение скорости. Его легко найти, когда закон движения задан в скалярной форме (1.2.3), продифференцировав его:
υ =
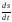 (1.2.8)
(1.2.8)
Скорость будет выражаться положительным числом при движении тела по траектории в положительном направлении и отрицательным при движении в отрицательном направлении.
Когда закон движения задан в координатной форме (1.2.2), то следует найти проекции вектора скорости на координатные оси как первые производные по времени от соответствующих координат, а затем найти модуль вектора скорости:
υx=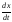 ,
υ y=
,
υ y=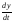 ,
υ z=
,
υ z=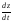 ,
v=
,
v=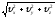 (1.2.9)
(1.2.9)
5. Ускорение
 характеризует быстроту изменения
скорости. На рис. 4 показаны два положения
на траектории движущейся частицы,
соответствующие им скорости
характеризует быстроту изменения
скорости. На рис. 4 показаны два положения
на траектории движущейся частицы,
соответствующие им скорости
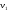 и
и
 ,
и приращение скорости
,
и приращение скорости
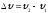 .
Вектор среднего ускорения
.
Вектор среднего ускорения 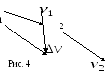
<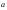 >=
>=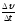 (1.2.10)
(1.2.10)
При уменьшении промежутка времени t и стремлении его к нулю предел выражения (1.1.10) дает определение мгновенного ускорения:
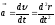 (1.2.11)
(1.2.11)
Из рис. 4
следует, что при движении по криволинейной
траектории вектор ускорения направлен
под углом к вектору скорости внутрь
траектории. При прямолинейном движении
вектор ускорения совпадает с вектором
скорости при ускоренном движении и
противоположен ему при замедленном.
Всякий вектор, в том числе и
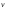 ,
имеет две характеристики – модуль и
направление, они могут изменяться
независимо друг от друга. Используя
формулы (1.2.7) и (1.2.11), получаем:
,
имеет две характеристики – модуль и
направление, они могут изменяться
независимо друг от друга. Используя
формулы (1.2.7) и (1.2.11), получаем:
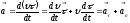 (1.2.12)
(1.2.12)
Вектор
ускорения состоит из двух слагаемых –
тангенциального
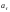 и нормального
и нормального
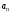 ускорений. Первое слагаемое –
тангенциальное ускорение – направлено
по касательной к траектории и указывает
на изменение модуля скорости. При
убыстрении движения
ускорений. Первое слагаемое –
тангенциальное ускорение – направлено
по касательной к траектории и указывает
на изменение модуля скорости. При
убыстрении движения
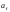 и
и
 направлены в одну сторону, при замедлении
они противоположны. Величина
тангенциального ускорения
направлены в одну сторону, при замедлении
они противоположны. Величина
тангенциального ускорения
a=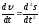 (1.2.13)
(1.2.13)
Второе
слагаемое – нормальное ускорение –
связано с изменением направления
скорости. Это хорошо известное из
школьного курса физики центростремительное
ускорение при равномерном движении
тела по окружности. Оно направлено по
радиусу к центру окружности и равно:
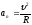 (1.2.14)
(1.2.14)
R
– радиус кривизны траектории, т.е.
радиус соприкасающейся окружности,
дугой которой можно заменить бесконечно
малый участок кривой в окрестности
данной ее точки. Задав в этой точке орт
нормали
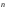 ,
направленный по радиусу окружности в
ее центр, получаем:
,
направленный по радиусу окружности в
ее центр, получаем:
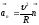 (1.2.15)
(1.2.15)
На рис 5 показан небольшой кусочек траектории, где в данный момент времени находится движущаяся частица. Орты касательный и нормали взаимно перпендикулярны, соответственно, перпендикулярны друг другу тангенциальное и нормальное ускорения, а полное ускорение равно:
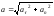 (1.2.16)
(1.2.16)
Если закон движения задан в координатной форме, то модуль ускорения можно вычислить аналогично модулю скорости (формула 1.2.9) так:
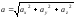 =
=
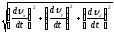 (1.2.17)
(1.2.17)
Для вычисления проекций вектора ускорения на оси координат можно воспользоваться формулами:
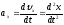 ,
,
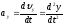 ,
,
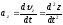 (1.2.18)
(1.2.18)
