3. Динамика вращательного движения

Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное.

При поступательном движении все точки тела в любой момент времени имеют одинаковые скорости и ускорения, вследствие чего перемещения всех точек тела равны друг другу.

При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Перемещения точек тела оказываются разными. Если твердое тело перемещается в пространстве и при этом вращается, то это сложное движение можно представить как сумму поступательного и вращательного движений, происходящих одновременно.

3.1. Кинетическая энергия вращающегося тела. Момент инерции твердого тела

Рассмотрим твердое тело, вращающееся вокруг некоторой неподвижной в пространстве оси ОО.

Рис.10

Мысленно разобьем объем тела на малые элементы и пронумеруем их от 1 до N. Выделим элемент тела массы m_i находящийся на расстоянии r_i от оси вращения (рис.10). Линейная скорость этого элемента v_i. Кинетическая энергия выбранного малого элемента тела

,

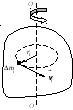
где  – угловая скорость вращения тела (одинакова для всех элементарных масс).

Для того чтобы найти кинетическую энергию всего вращающегося тела, необходимо просуммировать кинетические энергии отдельных элементов тела:

.

Введем обозначение:

. (15)

Эта физическая величина называется моментом инерции твердого тела относительно заданной оси вращения. Момент инерции является мерой инертности тела при вращательном движении и зависит от массы тела, его размеров и формы а также от пространственного положения оси вращения. Размерность момента инерции в СИ – кгм².

Таким образом, кинетическая энергия тела вращающегося вокруг фиксированной оси может быть выражена через момент инерции тела I и угловую скорость его вращения :

.

Если тело вращается и одновременно движется поступательно, то кинетическая энергия тела складывается из кинетической энергии поступательного движения центра масс и кинетической энергии вращательного движения.

.

3.2. Моменты инерции тел простой геометрической формы

Момент инерции твердого тела относительно некоторой оси вращения определяется выражением (15):

.

Суммирование распространяется на элементы всего твердого тела. Если разбиение тела проводить на все более и более мелкие элементы, то тогда сумма в пределе трансформируется в интеграл, и в результате чего получим:

(16)

(интегрирование ведется по всему объему твердого тела).

Можно получить еще одну формулу полезную для расчета момента инерции. Для этого воспользуемся выражением для плотности вещества: . После подстановки dm = dV в (16) получим:

. (17)

В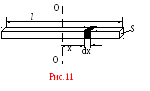 качестве примера применения формулы (16) найдем момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину (рис.11). Длина стержня l, масса стержня т. Разобьем весь стержень на отрезки малой длины . Масса такого отрезка равна , а расстояние до оси вращения r = x. Момент инерции всего стержня найдем, воспользовавшись формулой (16):

Рис.12

.

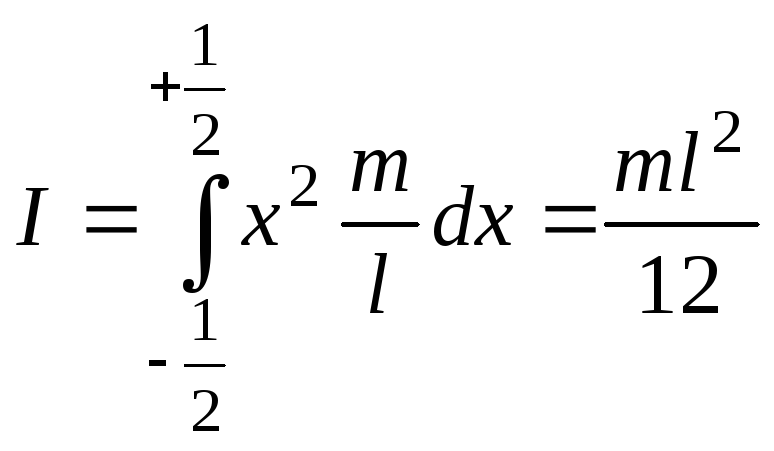Приведем, для справок, формулы для моментов инерции тел простейшей геометрической формы.

 Момент инерции однородного диска (рис.12) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр равен:

,

где радиус диска R, масса т.

Рис.13

Эта же формула справедлива и для момента инерции сплошного цилиндра относительно оси совпадающей с осью

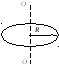
цилиндра.

 Момент инерции тонкого обруча относительно оси, перпендикулярной к плоскости обруча и проходящей через его центр будет (рис.13):

.

где радиус обруча – R, масса обруча – т.

Эта же формула справедлива для тонкостенного цилиндра.

 Момент инерции шара относительно оси проходящей через его центр. Радиус шара R, масса т:

.

 Момент инерции тонкого диска массы m и радиуса R, (толщина диска b << R), относительно оси совпадающей с диаметром диска:

:

,

Все приведенные формулы справедливы для моментов инерции относительно оси проходящей через центр масс (центр инерции) твердого тела. Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера:

Момент инерции относительно произвольной оси О₁О₁ равен сумме момента инерции I₀, относительно оси OO, параллельной данной и проходящей через центр инерции тела (центр масс тела) и произведения массы тела на квадрат расстояния между осями.

.

Рис.14

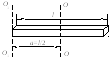
В качестве примера получим с помощью этой теоремы выражение для момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через один из его концов (рис.14). Из рисунка ясно, что а = , кроме этого момент инерции относительно оси, проходящей через центр масс равен:

Поэтому по теореме Штейнера получим:

.