1.3. Ускорение при криволинейном движении – тангенциальное и нормальное ускорения

Скорость является вектором, т.е. характеризуется как величиной, так и направлением. При криволинейном движении скорость может изменяться независимо как по величине, так и по направлению. Поэтому ускорение содержит две составляющие (рис.3).

Тангенциальное а_t (касательное) ускорение характеризует изменение модуля скорости и равно производной от модуля мгновенной скорости по времени

.

Направлено тангенциальное ускорение по касательной к траектории (так же как и вектор скорости). Если модуль скорости увеличивается, то тангенциальное ускорение положительно, если уменьшается, то отрицательно.

Нормальное (центростремительное) ускорение а_n характеризует изменение направления скорости и по величине равно

,

где R – радиус кривизны траектории.

Вектор нормального ускорения перпендикулярен скорости и направлен к центру кривизны траектории (рис.3).

Как видно из рисунка полное ускорение можно определить по теореме Пифагора и оно равно:

.

Полное ускорение направлено также как сила, действующая на тело, и определяется вторым законом Ньютона.

1.4. Кинематика вращательного движения

Рассмотрим материальную точку М, вращающуюся вокруг оси ОО (рис.4).

Пусть в некоторый момент времени t она находится в положении М, а в момент времени t + dt – в положении М'. За малое время dt радиус-вектор повернется на угол dj и материальная точка пройдет путь dS по окружности.

Величину dS можно выразить через угол dj и радиус окружности r:

.

Поделим обе части уравнения на dt:

. (4)

Величина, стоящая в левой части равенства представляет собой модуль скорости . Производная от j по t в правой части равенства называется угловой скоростью:

. (5)

Угловая скорость w характеризует быстроту изменения угла поворота вращающейся точки и измеряется в радианах за секунду (рад/с).

Для полной характеристики вращательного движения недостаточно знать только численное значение угловой скорости. Надо задать еще положение в пространстве оси вращения и направление вращения вокруг этой оси. Для этого необходимо угловую скорость считать векторной величиной. Направление вектора угловой скорости связано с направлением вращения правилом правого винта (правилом буравчика). Согласно этому правилу вектор мгновенной угловой скорости всегда направлен по оси вращения, в ту или другую сторону в зависимости от направления вращения (рис.5).

Рис.5

Из уравнений (4) и (5) следует связь между величинами мгновенной скорости и угловой скорости w

.

Так как линейная и угловая скорости являются векторами, то связь между ними можно записать также в форме векторного произведения

.

Рассмотрим теперь равномерное вращательное движение.

При таком движении величина угловой скорости остается постоянной w = const, и из формулы (5) следует

. (6)

Чтобы найти связь  и  за конечный промежуток времени необходимо проинтегрировать выражение (6)

.

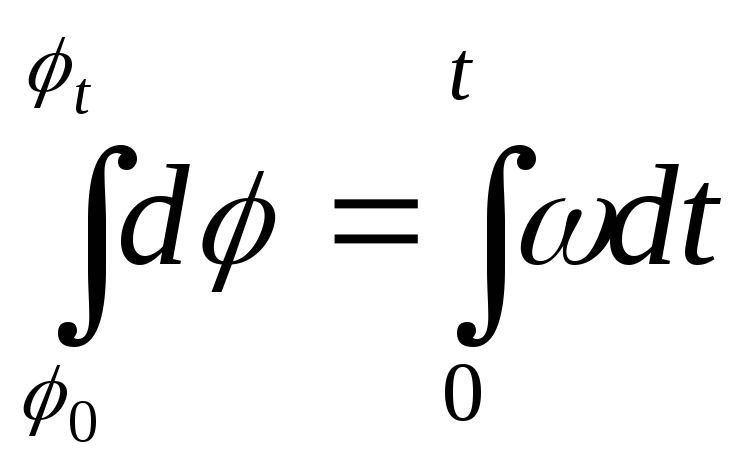Так как  = const, то ее можно вынести за знак интеграла и в результате интегрирования получи

, или ,

где – угол поворота в начальный момент времени и в момент времени t.

Эта формула верна только для вращательного движения по окружности с постоянной угловой скоростью.

Для такого движения можно ввести понятие периода обращения Т. Период Т – это время, затрачиваемое на один полный оборот. Величина обратная периоду называется частотой n. В системе СИ период измеряется в секундах, а частота в Герцах (Гц). Один Герц соответствует одному обороту за секунду.

За время, равное T, материальная точка совершает полный оборот, т.е. проходит угол j = 2p (рад). Тогда, из соотношения (6) получим:

,

где  – частота вращения выраженная в Гц.

Если вращение происходит неравномерно, то быстроту изменения угловой скорости можно характеризовать угловым ускорением e

.

Угловое ускорение измеряется в рад/с².

Величина тангенциальной составляющей ускорения материальной точки при движении по окружности связана с угловым ускорением следующим образом:

.

Величина нормальной составляющей ускорения (центростремительное ускорение) равно:

.

Если угловое ускорение не меняется с течением времени (), то

; (7)

, (8)

где , – угловые скорости вращения в начальный момент времени и в момент времени _.

Угловое ускорение алгебраическая величина: для равноускоренного вращения, и для равнозамедленного вращения.

Формулы (7,8) полностью описывают вращательное движение с постоянным по величине угловым ускорением. Легко заметить, что они аналогичны формулам для скорости и пути при прямолинейном равноускоренном движении. Сравнение формул для этих движений представлено в таблице:

Прямолинейное ускоренное движение	Вращательное ускоренное движение
Скорость	Угловая скорость
Путь	Угол поворота