6.6. Сложение взаимно-перпендикулярных колебаний. Фигуры Лиссажу

Предположим, что материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях с одинаковыми частотами:

x = А₁cos(t + ₁); y = А₂cos(t + ₂).

Траектория результирующего колебания будет зависеть от разности фаз складываемых колебаний.

В общем случае траектория колеблющейся точки – эллипс:

. Рассмотрим некоторые частные случаи:

1) ₂ -₁=   k, то эллипс становится отрезком прямой. (k – целое число);

2) ₂-₁ =( k  /2) и А₁ = А₂, то эллипс превращается в окружность (k – целое число);

3) в общем случае, при произвольном соотношении фаз и амплитуд, отличном от приведенных выше, траектория – эллипс.

Если взаимно-перпендикулярные колебания происходят с различными частотами, то в результате сложения получаются траектории более сложной формы, называемые фигурами Лиссажу. Форма фигур Лиссажу зависит от соотношения частот, разности фаз складываемых колебаний и от амплитуд колебаний что используется на практике для измерения этих величин.

6.7. Затухающие колебания

Вследствие сопротивления движению колебательная система непрерывно отдает часть своей энергии среде. При убывании энергии колебаний уменьшается и амплитуда колебаний, т.е. колебания затухают.

Рассмотрим случай, когда материальная точка совершает прямолинейное колебание под действием упругой силы, двигаясь в вязкой среде. При малых скоростях в вязкой среде сила трения пропорциональна скорости v:

,

где r – коэффициент сопротивления.

Кроме этой силы действует упругая сила (закон Гука)

.

Результирующая сила равна сумме упругой силы и силы трения.

Следовательно, уравнение движения (по II закону Ньютона) имеет вид:

; .

Введем обозначения:

.

где  – коэффициент затухания ( > 0); ₀ – частота колебаний этой же системы в отсутствии затухания. Уравнение затухающих колебаний с учетом введенных обозначений будет иметь следующую форму:

.

Общее решение этого уравнения может быть записано в следующем виде:

,

где – амплитуда затухающих колебаний.

Как видно из последней формулы, амплитуда колебаний с течением времени уменьшается и темп уменьшения определяется коэффициентом затухания .

Величина является циклической частотой затухающих колебаний; ₀ – циклической частотой колебаний этой же системы в отсутствии трения (циклическая частота собственных колебаний).

На рис.24 представлен график затухающих колебаний.

x

t

Рис.24

Для характеристики степени затухания колебаний используют не только коэффициент затухания , но и другие величины:

1) логарифмический декремент затухания;

2) время релаксации колебаний;

3) добротность системы.

Логарифмическим декрементом затухания называется натуральный логарифм отношения двух значений последовательных амплитуд:

,

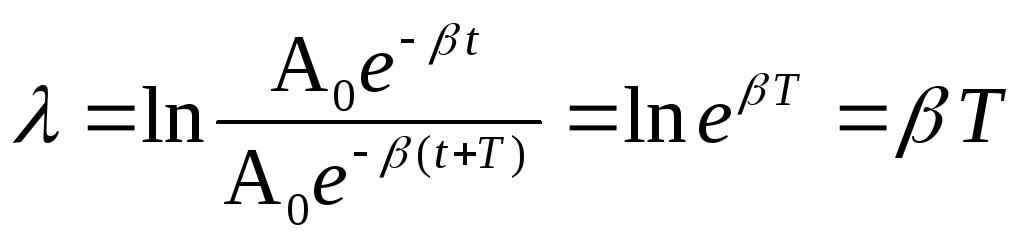где Т – период колебаний.

Связь между логарифмическим декрементом затухания, коэффициентом затухания и периодом колебаний

 = T.

Время релаксации – это время, в течение которого амплитуда убывает в e раз (е – основание натуральных логарифмов),

.

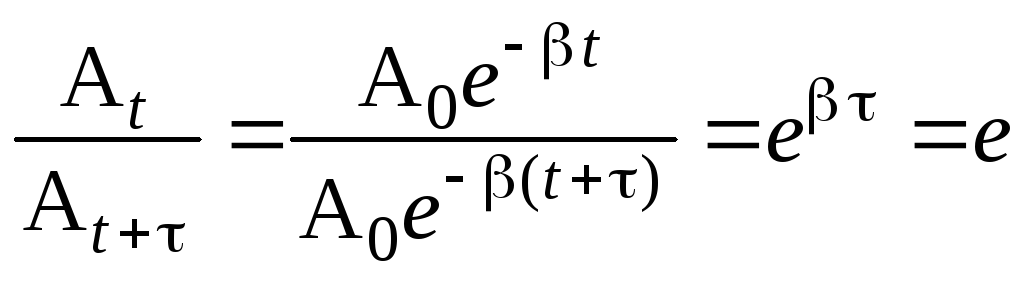Из последнего соотношения получим  = 1, т.е. коэффициент затухания есть физическая величина, обратная времени релаксации.

При практическом использовании колебаний важно, чтобы колебания затухали по возможности медленно. Величину, которая характеризует это свойство, называют добротностью. По определению добротность

.

Рассмотрим теперь важный для практики режим затухающих колебаний, когда  = ₀. В этом случае и движение становится апериодическим. Этот режим называется критическим, а – критическим сопротивлением.

На рис.25 представлен график апериодического движения.

Рис.25

Критический режим затухающих колебаний используется, например, в демпферах амортизационных систем автомобилей для уменьшения тряски при движении; в стрелочных электроизмерительных приборах для уменьшения амплитуды колебаний стрелки прибора при измерениях и в ряде других случаев.