5.6. Флуктуационный шум

Примером случайного процесса является флуктуационный шум, наиболее характерный для большинства каналов электросвязи. Для количественных расчетов воздействия флуктуационного шума на сигнал необходимо знать основные вероятностные характеристики. Поскольку шум образуется как сумма большого числа отдельных независимых колебаний, он, согласно центральной предельной теореме представляет собой стационарный эргодический случайный процесс с гауссовским (нормальным) распределением вероятности.

ПРВ гауссовского процесса описывается формулой [6, 32]:

в которую входят два числовых параметра m и σ² , имеющие смысл математического ожидания и дисперсии: m = M(x), σ² = D(X).

График плотности вероятности W(x) представляет собой колоколообразную кривую с единственным максимумом в точке x = m (рис. 5.11). Из графика видно, что с уменьшением σ кривая все более локализуется в окрестности точки x = m. Для флуктуационного шума обычно M(x) = 0.

Рис. 5.11. Гауссовское распределение вероятностей

Функция распределения вероятности для гауссовского случайного процесса:

После замены переменных y = (x - m)/σ эта функция приводится к виду:

где

–интеграл вероятности.

Функция Ф₀(z) табулирована в математических справочниках. Заметим, что Ф₀(-z) = -Ф₀(z) , Ф₀(0) = 0, Ф₀(∞) = 0,5. Для приближенных вычислений можно воспользоваться приближенным выражением:

Ф₀(z) ≈ 0,5 - 0,65 exp[-0,44(z + 0,75)²]

Пример. Вычислим вероятность того, что мгновенное значение флуктуационного шума с нулевым средним и дисперсией σ² = 9 [B²] превысит уровень x₀ = 6 [B].

Исходя из определения функции распределения вероятности, вероятность превышения случайным процессом уровня x₀

p(X > x₀) = 1 - p(X ≤ x₀) = 1 - F(x₀)

Подставляя значение F(x₀) для гауссовского случайного процесса, получаем:

p(X > x₀) = 1 - 0,5 - Ф₀[(x₀ - m)/σ] = 0,5 - Ф₀[(x₀ - m)/σ]

Для заданных числовых значений и m = 0, воспользовавшись таблицами или приближенной формулой для Ф₀(z), получаем:

p(X > 6) ≈ 2,33∙10^-2.

Обычно спектральная плотность мощности G_x(f) флуктуационного шума постоянна в широком диапазоне частот, т. е. можно приближенно считать, что: G_x(f) = N₀ при 0 ≤ f ≤ ∞. В этом случае шум называют белым. Это название дано по аналогии с белым светом, имеющим все частотные компоненты.

6. Комплексное представление сигналов и помех

6.1. Понятие аналитического сигнала

Представление детерминированных сигналов рядами ортогональных функций полезно при анализе прохождения сигналов через линейные радиотехнические устройства.

При анализе нелинейных преобразований сигналов и, в частности, модуляции и демодуляции, требуется иной подход. Этот подход основывается на понятии аналитического сигнала.

Многие формулы гармонического анализа записываются значительно проще и некоторые задачи решаются легче, если использовать в качестве элементарных функций экспоненциальные функции мнимого аргумента, например комплексная огибающая легко отделяется от множителя с несущей частотой при выражении сигнала в комплексной форме.

A∙cos[j(ω₀t + φ)] = [А∙ехр(j φ)]∙ехр (ω₀t).

Если разложить косинус суммы по формуле Эйлера [6, 21], то:

cos(ωt + φ) = 1/2[exp{j(ωt + φ)} + exp{-j(ωt + φ)}]. (6.1)

Этой записи можно дать геометрическую трактовку, пользуясь представлением комплексных чисел в виде точек или векторов на плоскости.

Выражение exp{j(ωt + φ)} представляет в данном случае вектор единичной длины, проведенный под углом ωt + φ к действительной оси (рис. 6.1). При изменении времени t этот вектор единичной длины меняет положение, вращаясь в положительном направлении с угловой скоростью ω.

Изобразить синусоиду в форме (6.1), это значит представить ее суммой двух векторов, длина каждого из которых равна 1/2, расположенных в любой момент времени симметрично относительно действительной оси и вращающихся в разных направлениях с угловыми скоростями ω и -ω (рис. 6.2).

Рис. 6.1. Геометрическая трактовка Рис. 6.2. Экспоненциальное

трактовка экспоненциальной ф-ции представление элементарной

мнимого аргумента функции

В момент t = 0 они занимают положения под углами φ и –φ относительно действительной оси. Геометрическая сумма векторов всегда совпадает по направлению с действительной осью и представляет действительную функцию времени cos(ωt + φ).

При представлении косинусоиды в виде cos(ωt + φ) = Re[exp{j(ωt + φ)}] можно ограничиться одним вращающимся в положительном направлении вектором и представить косинусоиду его проекцией на действительную ось.

В этом случае нет необходимости вводить отрицательные частоты. Длина вектора представляет амплитуду косинусоиды, а угол, образуемый им в данный момент с действительной осью – полную фазу (ωt + φ).

Проекция этого вектора на мнимую ось равнаIm[exp{j(ωt + φ)}] = sin (ωt + φ), т.е. представляет ту же косинусоиду, сдвинутую по фазе на π/2 (рис. 6.3).

Значительное количество сигналов применяемых в системах электросвязи можно представлять в виде:

s(t) = A(t)∙cos[ωt + φ(t)] (6.2)

т.е. как «квазигармоническую» функцию с переменными «амплитудой» и «начальной фазой».

Рис. 6.3. Проекции единичного

вектора на действительную и

мнимую оси

Такой сигнал можно интерпретировать геометрически как проекцию на действительную ось вращающегося вектора, но при этом изменяющего свою длину и угловую скорость. Для описания свойств сигнала представленного в форме (6.2) вводят понятие комплексного аналитического сигнала.

Аналитический сигнал формируется путем отбрасывания области отрицательных частот спектра вещественного сигнала и удвоения спектра в области положительных частот. Так, если s(t) – вещественный сигнал, записываем s(t) ↔ S(f) и аналитический сигнал

s_a(t) ↔ 2σ(f)∙X(f), (6.3)

где σ(f) – единичная ступенчатая функция в частотной области.

Единичная ступенчатая функция равна нулю в интервале от минус бесконечности до некоторой точки и единице в интервале от этой точки до плюс бесконечности. Ступенчатая функция во временной области имеет вид

(6.4)

Преобразование Фурье единичной ступенчатой функции равно

(6.5)

Таким образом, можно определить единичную ступенчатую функцию в частотной области и ее преобразование Фурье. Пусть

тогда

(6.6)

Заметим, что если s(t) – синусоида постоянной амплитуды, то операция, указанная в выражении (6.3), состоит просто в замене вещественной синусоиды комплексной экспонентой. В более общем случае для нахождения вещественной и мнимой частей s_a(t) можно преобразовать спектр в выражении (6.3) во временную область:

(6.7)

Свертка s(t) с импульсной функцией не меняет s(t), поэтому можно записать

(6.8)

Вещественная часть s_a(t) является исходной вещественной функцией, а мнимая часть определяется в формуле (6.8) интегралом от функции, содержащей s(t). Этот интеграл называется преобразованием Гильберта функции s(t) и обозначается

(6.9)

Существует следующее обратное соотношение:

(6.10)

Таким образом, s(t) и s*(t) представляют собой пару преобразований Гильберта и аналитический сигнал можно записать как

s_a(t) = s(t) + js*(t). (6.11)

Исходя из этого, аналитический сигнал в момент времени t может быть представлен точкой на комплексной плоскости, если по оси абсцисс откладывать значения реального сигнала s(t), а по оси ординат – сопряженного с ним сигнала s*(t), (рис. 6.4).

Легко показать, что функция sin(ω₀t) является преобразованием Гильберта cos(ω₀t). Поэтому аналитический сигнал, соответствующий cos(ω₀t), имеет вид s_а(t) = cos ω₀t + j sin ω₀t = =exp(jω₀t). Аналитический сигнал общего вида удобно представлять в экспоненциальной форме как

s_a(t) = |s_a(t)|exp [jФ(t)], (6.12)

где |s_a(t)| = [s²(t) + j∙s*²(t)]^1/2;

Ф(t) = arctg [s*(t)/s(t)].

Рис. 6.4. Представление аналитического

сигнала точкой

Теперь положим Ф(t) = ω₀t + φ(t) и запишем

s_a(t) = |s_a(t)| ехр [jφ(t)] ехр (jω₀t) = (t) exp (jω₀t) (6.13)

Комплексная огибающая (t) получается удалением комплексного множителя, связанного с несущей, из аналитического сигнала:

(t) = s_a(t)∙ехр (-jω₀t) = |s_a(t)| ехр [jφ(t)]. (6.14)

Если (t) – узкополосная относительно f₀ функция, то она будет обладать свойствами, которые мы интуитивно связываем с огибающей. В противном случае это просто удобное математическое представление.

Для получения спектра функции s*(t) можно применить функцию sign, которая тесно связанной с единичной ступенчатой функцией и определяется как

(6.15)

Соотношение между функцией sign и единичной ступенчатой функцией σ(t) показано графически на рис. 6.5.

Рис. 6.5. Единичная ступенчатая функция σ(t) и функция sign (t)

Функция sign может быть определена и в частотной области sign (f). С помощью выражений (6.5) и (6.15) получаются следующие соотношения для пар преобразований:

Функция sign может быть определена и в частотной области sign (f). С помощью выражений (6.5) и (6.15) получаются следующие соотношения для пар преобразований:

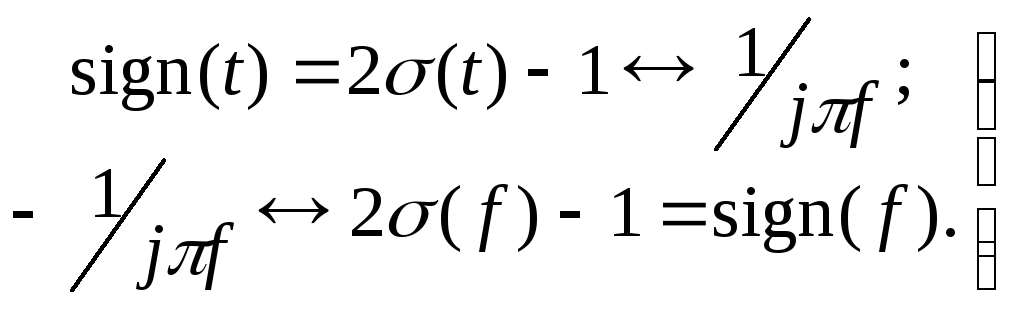(6.16)

Таким образом, спектр функции s*(t) имеет вид:

l/πt ↔ -j∙sign (f);

(6.17)

С помощью обобщения теоремы Парсеваля можно показать, что s(t) и s*(t) ортогональны. Для двух заданных функций s₁(t) и s₂(t) обобщенное соотношение Парсеваля состоит в том, что

(6.18)

откуда

(6.19)

но S(f)[ -j∙sign (f)∙S(f)]* = j| S(f)|² ∙ sign (f).

В силу того, что эта функция частоты нечетна, интеграл в выражении (6.19) по всему частотному диапазону равен нулю. Поэтому

Спектральные плотности энергии s(t) и s*(t) одинаковы, следовательно, полная энергия аналитического сигнала в два раза больше энергии вещественного.