Соответствие синдромов конфигурациям ошибок

Синдром	001	010	011	100	101	110	111
Конфигурация ошибок	0000001	0000010	0001000	0000100	1000000	0010000	0100000
Ошибка в символе	k3	k2	i4	k1	i1	i3	i2

Таким образом, код (7,4) позволяет исправить все одиночные ошибки. Простая проверка показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно создание такого цифрового корректора ошибок (дешифратора синдрома), который по соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.

Циклические коды. Циклическим кодом называется такой групповой код, который связан дополнительным условием цикличности. Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода.

Циклические коды широко применяются при передаче данных в современных информационных системах благодаря ряду положительных качеств, основными из которых являются:

- высокая эффективность, так как циклические коды обладают сравнительно небольшой избыточностью, отличаются простотой реализации кодирующих и декодирующих устройств;

- высокая помехоустойчивость – за счет способности кода к обнаружению и исправлению ошибок.

Для оптимального кода количество исправляемых ошибок равно 2^k-1, где k – число контрольных разрядов.

Применяемые в настоящее время циклические коды, содержащие n разрядов, из которых m является информационными, а k = n-m – контрольными (проверочными), расположенными в конце кодовой комбинации. Так как информационные и контрольные разряды занимают строго определенные места и длина кодовой комбинации постоянна, то циклические коды относятся к систематическим кодам.

Для описания циклических кодов обычно пользуются записью любого n-разрядного двоичного числа в виде многочлена степени (n-1). Например, кодовая комбинация 1011001 записывается как многочлен x⁶ + x⁴ + x³ + 1, т.е. коэффициенты многочлена не пишутся, а члены с коэффициентами 0 опускаются. Наивысшая степень числа с коэффициентом 1 называется степенью полинома (многочлена). Так, в примере рассмотрен многочлен 6-й степени.

Таким образом, действия над кодовыми числами можно свести к действиям над многочленами. При этом используют теорию коммутативных колец. Коммутативным кольцом называют множество, в котором особым образом определены операции сложения и умножения.

В циклическом кодировании все математические операции сложения производятся с использованием сложения по mod 2 и с приведением подобных членов.

Операцию умножения символически проводят по следующим правилам:

1) Вначале все многочлены перемножаются по обычным правилам, но с приведением подобных членов по mod 2.

2) Если старшая степень полученного в результате умножения многочлена не превышает (n-1), то этот многочлен является результатом символического умножения.

3) Если старшая степень полученного в результате умножения многочлена больше (n-1), то многочлен произведения делится на двучлен xⁿ+1. В этом случае результатом символического умножения считается остаток от деления (вычет).

Пример: Имеем кодовые комбинации 001101 и 101110, где n = 6.

Эти комбинации соответствуют многочленам: x³ + x² + 1 и x⁵ + x³ + x² + x.

Допустим, необходимо провести дважды циклический сдвиг этих кодовых комбинаций. В результате получим:

Для проведения этой операции с многочленами необходимо их символически умножить на x×x = x²:

1) (x³ + x² + 1) × x² = x⁵ + x⁴ + x², т.к. степень полученного многочлена не превышает (n-1) = 5, то этот многочлен принимается за результат умножения и действительно соответствует сдвинутой кодовой комбинации 110100.

2) (x⁵ + x³ + x² + x) × x² = x⁷ + x⁵ + x⁴ + x3, т.к. степень полученного многочлена превышает (n-1), то для получения результата символического умножения необходимо произвести деление этого многочлена на двучлен (xⁿ +1):

Остаток от деления x⁵ + x⁴ + x³ + x принимается за результат символического умножения, что соответствует циклически сдвинутой кодовой комбинации 111010.

В основе образования циклического кода лежит использование так называемого образующего (неприводимого) многочлена (полинома). Выбор образующего полинома определяет тип циклического кода и характеризует его обнаруживающие и исправляющие способности.

Степень образующего полинома равна k, т.е. числу контрольных символов. Любой многочлен циклического кода должен делиться без остатка на образующий полином.

В то же время ни один многочлен, соответствующий запрещенной кодовой комбинации, не должен делиться без остатка на образующий полином. Это свойство позволяет обнаружить ошибку, а по виду остатка и вектор ошибки, т.е. исправлять ошибки.

Для получения циклического кода, многочлен G(x) (соответствующий кодовым комбинациям безызбыточного m – разрядного кода), умножают на x^k. Это соответствует приписыванию со стороны младших разрядов k нулей к кодовым комбинациям.

Затем произведение G(x)×x^k делится на образующий многочлен Р(x). В общем случае мы получаем в результате такого деления Q(x) той же степени, что и G(x) и остаток R(x). Остаток R(x) прибавляется к G(x)×x^k. Получаем многочлен F(x) = G(x)×x^k + R(x).

Так как в комбинациях, соответствующих многочлену G(x)×x^k, первые k младших разрядов – нули, а R(x) – многочлен степени не выше k-1, то операция получения многочлена соответствует приписыванию R(x) к G(x) со стороны младших разрядов.

Полученный таким образом многочлен F(x) будет делиться на образующий многочлен Р(x) без остатка.

Таким образом, циклический код можно получить, если к каждой кодовой комбинации безызбыточного кода приписывать остаток от деления многочлена, соответствующего этой кодовой комбинации на образующий многочлен.

Так как опознавателями ошибок являются остатки от деления многочленов циклического кода на образующий многочлен, то корректирующая способность кода будет тем выше, чем больше остатков от деления можно образовать. Наибольшее число остатков, равное 2^k-1 (исключая нулевой), может обеспечить неприводимый (простой) многочлен, т.е. такой многочлен, который делится только сам на себя. Поэтому в качестве образующего многочлена необходимо выбирать простой многочлен (или их произведение).

Пример образования циклического кода. Пусть информационный код содержит m = 4 разрядов. Одна из N = 2^m комбинаций этого кода: 1101 в виде многочлена запишется так: G(x) = x³ + x² + 1.

Если циклический код обнаруживает и исправляет одну ошибку, его минимальное кодовое расстояние равно: d_min = S + r + 1 = 3 (где r - число обнаруживаемых, а S - число исправляемых ошибок).

Выберем из Таблицы 16.2 значение k (для m = 4, k = 3).

Выберем из таблицы 16.3 полином P(x) для k = 3: P(x) = x³ + x + 1 (т.е. 1011)

Умножим G(x) на x^k : G(x)×x³ = (x³ + x² + 1)×x³ = x⁶ + x⁵ + x³ (т.е. 1101 × 1000 = 1101000)

Разделим G(x)×x^k на полином P(x):

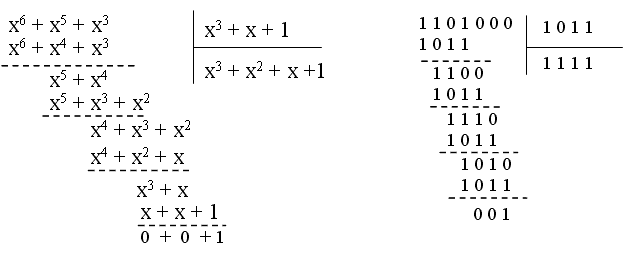
В результате получаем: G(x)×x³/ P(x) = (x³ + x² + x + 1) + 001/ (x³ + x + 1) или: 1111 + 001 / 1011

В соответствии с n = m + k: (x³ + x² + x + 1) = Q(x) → 1111

1/(x³ + x + 1) = R(x) / P(x) → 001 / 1011

R(x) = 001

Искомый многочлен F(x) равен:

F(x) = Q(x) × P(x) = G(x) × x^k + R(x) = x⁶ + x⁵ + x³ + 1 → 1101001

Для обнаружения и исправления ошибок принятая комбинация делится на образующий многочлен P(х). Если остаток R(х) = 0, значит, комбинация принята без ошибок. Наличие остатка свидетельствует о том, что комбинация принята искаженной.

Таблица 16.2