12.3. Цепи с конечной импульсной характеристикой (ких-цепи)

Предположим, что импульсная характеристика некоторой цепи h[n] имеет конечную длину N, т.е. h[n] ≠ 0, 0 ≤ n ≤ N - 1. Тогда свертка (12.10) принимает вид конечной суммы

и может быть записана в виде разностного уравнения

y[n] = b₀x[n] + b₁x[n - 1] + b₂x[n - 2] + … + b_{N -1}x[n - N + 1]. (12.12)

Вычисление каждого значения выходного сигнала требует учета текущего и N - 1 предшествующих отсчетов входного сигнала и может быть выполнено цепью, структурная схема которой показана на рис. 12.3. Такие цепи называются трансверсальными, или цепями с конечной импульсной характеристикой (КИХ-цепями).

Рис. 12.3. Структура цепи с конечной импульсной характеристикой

Комплексная частотная характеристика КИХ-цепи имеет вид полинома порядка N - 1 относительно e^-jω:

Таким образом, КИХ-цепь умножает спектральную плотность входной последовательности на полином.

12.4. Рекурсивные цепи

Другой важный для практики класс дискретных ЛИС-цепей составляют цепи, которые не умножают, а делят спектральную плотность входной последовательности на полином некоторого порядка M - 1 относительно e^-jω. Обозначим этот полином A(e^jω) = α₀ + α₁e^-jω + α₂e^-j∙2ω + … + α_M-1e^-j∙(M-1)ω, тогда спектральные плотности входной и выходной последовательностей связаны выражением Y(e^jω) = X(e^jω) / A(e^jω), следовательно, X(e^jω) = Y(e^jω) A(e^jω), откуда по аналогии с (12.3) можно записать

x[n] = α₀y[n] + α₁y[n - 1] + α₂y[n - 2] + … + α_M-1y[n - M + 1].

Решая это уравнение относительно выходного сигнала, получаем

откуда, вводя обозначения b = 1/α₀, α_i = -α_i/α₀, находим окончательно разностное уравнение рекурсивной цепи

y[n] = bx[n] + α₁y[n - 1] + α₂y[n - 2] + … + α_M-1y[n - M + 1],

структура которой показана на рис. 12.4.

Рис. 12.4. Структура рекурсивной цепи

12.5. Устойчивость лис-цепей

Обычно к ЛИС-цепям предъявляется требование устойчивости. Напомним, что линейная цепь называется устойчивой, если отклик на воздействие, ограниченное по модулю, также ограничен.

Для устойчивости ЛИС-цепи необходимо и достаточно, чтобы ее импульсная характеристика была абсолютно суммируемой, т.е. выполнялось условие [7]

(12.13)

Очевидно, для импульсных характеристик конечной длины это условие выполняется всегда, поэтому КИХ-цепи всегда устойчивы.

Рекурсивные цепи могут быть неустойчивыми из-за наличия обратных связей. Анализ устойчивости ЛИС-цепей основан на использовании z-преобразования, которое формально может быть получено из преобразования Фурье заменой величины e^jω на комплексное переменное z:

(12.14)

z-преобразование может сходиться для одних значений комплексного переменного z и расходиться для других. Множество точек комплексной z-плоскости, в которых z-преобразование сходится, называется областью сходимости. Для абсолютно суммируемой импульсной характеристики область сходимости ее z-преобразования содержит единичную окружность. Если цепь является физически реализуемой (каузальной), то она устойчива в том и только в том случае, если все полюсы ее передаточной функции

по модулю меньше единицы, т.е. находятся внутри единичной окружности.

Самый широкий класс ЛИС-цепей конечного порядка образуют цепи, структура которых может быть сведена к каскадному соединению трансверсальной и рекурсивной частей, что соответствует разностному уравнению вида

y[n] = b₀x[n] + b₁x[n - 1] + b₂x[n - 2] + … + b_N-1x[n - N + 1] +

+ α₁y[n - 1] + α₂y[n - 2] + … + α_M-1x[n - M + 1] =

(12.15)

откуда следует выражение для КЧХ дробно-рационального вида

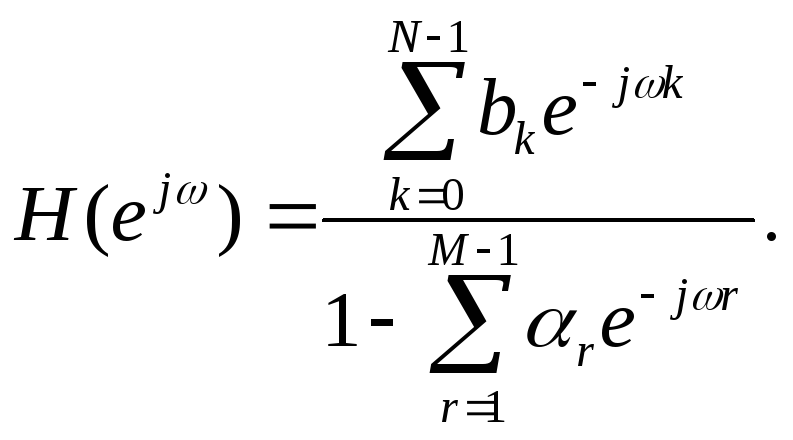(12.16)

В общем случае ЛИС-цепь конечного порядка с КЧХ вида (12.16) имеет бесконечно длинную импульсную характеристику (БИХ), но если полином-числитель делится на знаменатель без остатка, то результатом деления оказывается полином и импульсная характеристика имеет конечную длину (таковы, например, КИХ-фильтры на основе частотной выборки, см. далее).