3. Спектральные характеристики сигналов

3.1. Спектральное представление периодических сигналов

Как известно, разложение периодического сигнала по базису тригонометрических функций – это разложение его в ряд Фурье.

Разложение сигнала в ряд Фурье называется спектром сигнала.

В общем случае периодический сигнал содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, или гармоник, с частотами, кратными основной частоте последовательности.

Графическое изображение коэффициентов ряда Фурье для конкретного сигнала называется спектральной диаграммой. По горизонтальной оси откладываются частоты гармоник, а по вертикали – амплитуды (амплитудная диаграмма) или начальные фазы (фазовая диаграмма).

При разложении в комплексный ряд Фурье:

(3.1)

где

Спектр сигнала содержит компоненты на отрицательной полуоси частот, причём С_-k = С_k* (* обозначено комплексно-сопряжённое число).

Между коэффициентами комплексного и тригонометрического ряда существует связь:

(3.2)

Шириной спектра сигнала ΔF_э называется полоса частот, в пределах которой заключена основная доля энергии сигнала.

В качестве примера рассчитаем спектр периодической последовательности прямоугольных импульсов c амплитудой А:

Рис. 3.1. Периодическая последовательность прямоугольных импульсов

Определим коэффициенты разложения в ряд Фурье C_к:

, т.к. подынтегральная функция – нечетная.

Пусть Т = 2, тогда коэффициенты a_k равны:

a₀ = А, a_k = 2А/ k (sin k/2), при k > 0.

Итак, временная диаграмма периодической последовательности импульсов показана на рис. 3.1. Спектр этой последовательности дискретный и показан на рис. 3.2.

Рис. 3.2. Спектр периодическая последовательность прямоугольных импульсов

Ширина спектра сигнала равна, в данном случае, ΔF_э =2/.

3.2. Спектральное представление непериодических сигналов

Для спектрального представления непериодических (импульсных) сигналов s(t), заданных на конечном интервале (t₁, t₂) (рис. 3.3), непосредственно воспользоваться рядом Фурье нельзя. Для гармонического разложения сигнала мысленно дополняют его такими же импульсными сигналами до периодического с некоторым интервалом Т (рис. 3.3).

Рис. 3.3. Импульсный сигнал s(t) и его периодическое продолжение s_пер(t+kT)

Для того чтобы вне искусственно введенного интервала исходный сигнал был равен нулю, необходимо увеличить период повторения импульсов.

В пределе, при увеличении периода ∞ → Т все импульсы уйдут право и влево в бесконечность и периодическая последовательность вновь станет одиночным импульсом.

Для вычисления спектра удобна симметричная комплексная форма ряда Фурье, но в нем вместо суммы будет интеграл с бесконечными пределами (преобразование Фурье):

(3.3)

При таком предельном переходе основная частота сигнала Ω = 2π/T стремится к нулю, бесконечно увеличивается число спектральных составляющих, частоты соседних гармоник kΩ и (k + 1)Ω становятся неразличимыми, а спектр будет сплошным.

Функция G(jΩ) называется спектральной плотностью сигнала х(t).

Функции G(jΩ) и s(t) представляют собой две математические модели одного и того же физического процесса: одна из них отражает частотный состав сигнала, а другая описывает изменение сигнала с течением времени.

Спектральная плотность сигнала определяется с использованием прямого преобразования Фурье:

(3.4)

Таким образом, формулы (3.3) и (3.4) называются соответственно обратным и прямым преобразованиями Фурье Они показывают взаимосвязь между сигналом s(t) и его комплексной спектральной плотностью G(jΩ).

Для одиночного прямоугольного импульса с амплитудой А и длительностью  на рис. 3.4 получим спектр S(jΩ) на рис. 3.5:

Это выражение с учетом формулы Эйлера можно переписать в виде

(3.5)

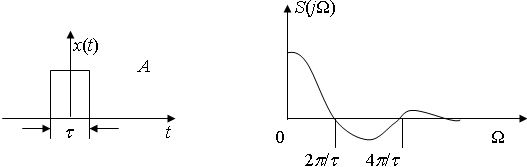
Рис. 3.4. Одиночный прямоугольный импульс Рис. 3.5. Спектр прямоугольного импульса

Спектр непериодического сигнала сплошной, бесконечный, ширина спектра определяется длительностью сигнала и, приближённо, равна ΔF_э ≈2/.