9.3. Перевірка гіпотези про закон розподілу. Критерій згоди Пірсона.

Критерієм згоди називають статистичний критерій перевірки гіпотези про закон розподілу ймовірностей випадкової величини (ознаки генеральної сукупності). Є кілька критеріїв згоди: критерій Колмогорова, критерій Смірнова, критерій Пірсона та ін.

Найбільш розповсюдженим критерієм перевірки вірогідності Hпро закон розподілу ознаки генеральної сукупності є критерій згоди Пірсона (критерій), який ґрунтується на порівнянні емпіричних і теоретичних частот та визначається за формулою, деm – число інтервалів, на які поділяється статистичний розподіл вибірки; n_і – частота ознаки в i –му інтервалі; п_і* – теоретичні частоти, підраховані за відповідними формулами закону розподілу ймовірностей, який припускається для ознаки генеральної сукупності.

Теоретичні частоти знаходяться за формулою , деn – об’єм вибірки; p_i – для дискретної випадкової величини є ймовірність події Х=х; для неперервної випадкової величини – ймовірність, що ознака Х попаде в і-ий інтервал.

Нехай висунуто гіпотезу H₀ : випадкова величина Х розподілена за законом А.

Здійснивши вибірку обсягу п, знаходять і записують у вигляді таблиці інтервальний статистичний розподіл частот:

				...
ni	n1	n2	n3	...	nm

Оскільки перевіряється гіпотеза про те, що розподіл ознаки Х генеральної сукупності описується певною (конкретною) функцією розподілу F(x), то для кожного інтервалу можна визначити теоретичні ймовірності p_i попадання значень випадкової величини Х у цей інтервал, а отже, і теоретичні частоти .

Для обчислення ймовірностей p_i використовують формули:

(26)

Зазначимо, що для обчислення ймовірностей p_i і p_m у формулі (26) покладають, відповідно, і . Тоді .

Отримані результати обчислень зручно записати у формі таблиці:

				...
ni	n1	n2	n3	...	nm
pi	p1	p2	P3	...	pm
	n1^*	n2^*	n3^*	...	nm^*

Згідно з критерієм Пірсона для перевірки гіпотези H₀ вводиться випадкова величина (статистика) K :

На підставі даних вибірки, записаних у таблиці, обчислюють емпіричне значення критерію Пірсона:

Відомо, що при n → ∞ закон розподілу статистики K прямує до закону розподілу зk=m−r−1 ступенями вільності, де m – кількість груп у статистичному розподілі вибірки; r − кількість параметрів гіпотетичного розподілу A (наприклад, r = 2 для нормального розподілу, r =1 для розподілу Пуассона, r =0 для рівномірного розподілу).

Для критерію будують правосторонню критичну область за правилом:

P_кр.= (27)

За заданим рівнем значущості α і кількістю ступенів вільності k із таблиці критичних точок розподілу (в якій дано розв’язки рівняння (27)) знаходять критичну точкуk_кр=(,k).

Порівнюємо значення k_кр і К_спост: якщо К_спост ≥ k_кр то гіпотезу H₀ відхиляють; якщо ж К_спост k_кр, то гіпотезу H₀ приймають.

Застосування критерію вимагає дотримання таких умов:

1) експериментальні дані мають бути незалежними, тобто вибірка має бути випадковою;

2) обсяг вибірки має бути достатньо великим (практично не меншим ніж 50 одиниць), а частота кожної групи – не меншою за 5. Якщо остання умова не виконується, то проводиться попереднє об’єднання нечисленних груп.

Критерій згоди Пірсона дає відповідь на питання, чи розбіжність між емпіричними і теоретичними частотами зумовлена випадковістю, чи вона є значущою. Як і будь-який інший критерій він не доводить справедливості гіпотези H₀, а лише дозволяє встановити на прийнятному рівні значущості узгодженість чи неузгодженість гіпотези H₀, з даними спостережень.

Приклад. При рівні значущості перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти

Емпіричні частоти, ni	7	14	39	75	107	86	31	15
Теоретичні частоти, пі*	4	15	43	83	100	77	38	14

Розв’язання

Складаємо таблицю для обчислення -критерію.

і		пі*
1	7	4	3	9	2,25	49	12,25
2	14	15	-1	1	0,07	196	13,06
3	39	43	-4	16	0,37	1521	35,37
4	75	83	-8	64	0,77	5625	67,77
5	107	100	7	49	0,49	11449	114,49
6	86	77	9	81	1,05	7396	96,05
7	31	38	-7	49	1,29	961	25,28
8	15	14	1	1	0,07	225	16,07
	374	374				27422	380,34

Контроль обчислень: – обчислення правильні.

Кількість ступенів вільності: s=8, k=s-3=5. За таблицею критичних точок -розподілу (додаток 4) за рівнем значущостіі кількістю ступенів вільностіk=5 знаходимо . Оскільки, то немає підстав відхилити нульову гіпотезу. Отже, розбіжність емпіричних та теоретичних частот незначуща, дані спостережень узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.

0. Перевірка гіпотези про рівність середніх двох сукупностей

Порівняння середніх двох сукупностей має важливе практичне значення. На практиці часто зустрічається випадок, коли середній результат однієї серії експерименту відрізняється від середнього результату другої серії. При цьому постає питання, чи можна пояснити таку різницю середніх випадковими неминучими помилками експерименту чи вона викликана деякими закономірностями.

В психолого-педагогічних дослідженнях задача порівняння середніх часто виникає при контролі, наприклад, рівня знань учнів, що навчалися за різними навчальними програмами або методиками, або в різних умовах і т.і.

Сформулюємо задачу.

Нехай маємо дві сукупності, що характеризуються генеральними середніми іівідомими дисперсіями інеобхідно перевірити гіпотезу Н₀ про рівність генеральних середніх, тобто Н₀ : =. Для перевірки гіпотези Н₀ із цих сукупностей взяті дві незалежні вибірки об’ємів п₁ і п₂ , по яких знайдено вибіркові середні іта вибіркові дисперсіїі.

При достатньо великих об’ємах вибірок вибіркові середні імають наближено нормальний закон розподілу, відповідноі.

У випадку справедливості гіпотези Н₀ різниця –має нормальний закон розподілу з математичним сподіванням М(–)=М()–М()=–=0 і дисперсією(дисперсія різниці незалежних випадкових величин дорівнює сумі їх дисперсій, а дисперсія середньоїп незалежних доданків в п раз менша дисперсії кожного).

Тому при виконанні гіпотези Н₀ статистика

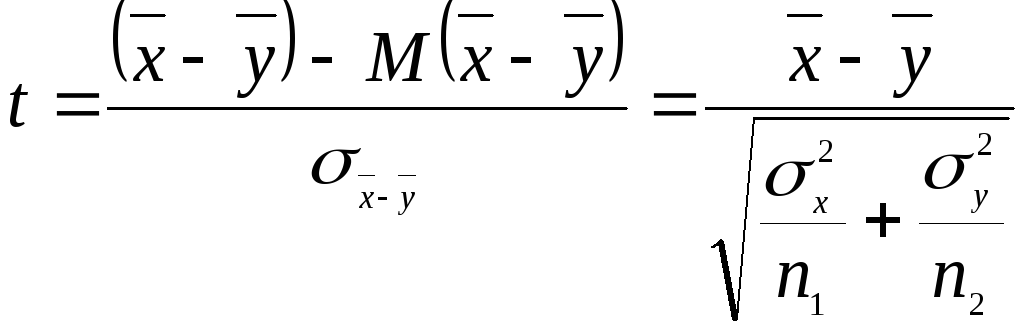(28)

має стандартний нормальний розподіл .

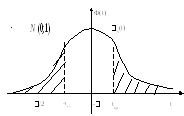
У випадку альтернативної гіпотези Н₁: >(або Н₁: ) вибирають односторонню критичну область і критичне значення статистики

(29)

а при конкуруючій гіпотезі Н₁: вибирають двосторонню критичну область і критичне значення статистики

(30)

Якщо спостережуване значення статистики t більше за t _кр, що визначене на рівні значимості  ( за абсолютною величиною), тобто t > t _кр, то гіпотеза Н₀ відхиляється. Якщо t  t _кр , то робиться висновок, що нульова гіпотеза не протирічить даним спостереження.

Приклад. Для перевірки ефективності нової методики навчання відібрано дві групи студентів. В першій групі чисельністю п₁ =50 студентів, де застосовувалася нова методика, середній бал успішності складав =85 балів, у другій чисельністюп₂ =70 студентів =78 балів. Попередньо встановлено, що дисперсії успішності в групах дорівнюють відповідно=100 і=74. На рівні значимості=0,05 потрібно з’ясувати вплив нової методики на середній бал успішності студентів.

Розв’язання

Припустимо, що середній бал успішності студентів при викладанні предметів за новою і старою методикою однакові, тобто Н₀ : =.

Тоді Н₁: >або Н₂: ( в даній задачі краще взяти Н₁, так як її справедливість означає ефективність застосування нової методики навчання).

За формулою (28) маємо .

При альтернативній гіпотезі Н₁ критичне значення статистики знаходиться з умови (29), тобто , звідки за таблицями значень функції Лапласаt _кр =t _0,9=1,64, а при Н₂ – умова (30), тобто , звідки t _кр =t _0,95=1,96.

Оскільки t > t _кр (при будь-якій із взятих конкуруючих гіпотез), то гіпотеза Н₀ відхиляється, тобто на 5%-ому рівні значимості можна зробити висновок, що нова методика дозволяє підвищити середній бал студентів.

Якщо припустити, що розподіл випадкових величин Х та У в кожній сукупності має нормальний закон розподілу, то тоді, якщо дисперсії івідомі, то перевірка гіпотез проводиться так, як описано вище, не тільки для великих але й для малих по об’єму вибірок. Якщо ж дисперсіїіневідомі, але рівні, тобто ==, то в якості невідомої величиниможна взяти її оцінку – виправлену вибіркову дисперсію

або.

Однак кращою оцінкою для буде дисперсія змішаної сукупності об’ємуп₁ + п₂, тобто

,

а оцінкою дисперсії різниці незалежних вибіркових середніх буде.

Доведено, що у випадку справедливості гіпотези Н₀, статистика

(31)

має t-розподіл Стьюдента з k=п₁+ п₂-2 ступенями вільності. Тому критичне значення статистики t знаходиться за формулами (29) і (30) в залежності від виду критичної області, в яких замість функції Лапласа Ф(t) береться функція ( t; k) для розподілу Стьюдента при k=п₁+п₂-2, тобто (t;k)=1-. при цьому зберігається те саме правило відхиляння (приймання) гіпотези: гіпотеза Н₀ відхиляється на рівні значимості , якщо t > t _1-2;k, (у випадку односторонньої критичної області) або t > t _1-;k (у випаду двосторонньої критичної області). У протилежному випадку гіпотеза Н₀ приймається.

Зауваження. Якщо дисперсії =невідомі і не передбачається, що вони рівні, то статистика, обрахована за формулою (31) також маєt‑розподіл Стьюдента, однак відповідне йому число ступенів вільності визначається наближено і складніше.

Приклад. Зроблено дві вибірки врожаю пшениці: при своєчасному зборі врожаю і зборі з деяким запізненням. У першому випадку при спостереженні 8 ділянок вибіркова середня урожаю склала 16,2ц/га, а середнє квадратичне відхилення – 3,2ц/га; у другому випадку при спостереженні 9 ділянок ті ж характеристики дорівнювали 13,9ц/га і 2,1ц/га. На рівні значимості =0,05 з’ясувати вплив своєчасного збору врожаю на середнє значення урожайності.

Розв’язання

Припустимо, що середнє значення урожайності при своєчасному зборі урожаю і з запізненням рівні, тобто Н₀ : =.

Тоді Н₁: >, що означає значний вплив на урожайність строків збору. За формулою (31),k=8+9-2=15 з умови (t;k)=1-2=1-2·0,05=0,9. Звідси за таблицею значень критерію Стьюдента (додаток 5) t_0,9;15=1,75. Оскільки t_0,9;15=1,75, то гіпотеза Н₀ приймається. Це означає, що дані які ми маємо на 5%-ому рівні значимості, не дозволяють вважати, що деяке спізнення у строках збору суттєво впливає на величину урожаю.

Порівняння середніх декількох сукупностей буде розглянуте у темі 11.

0. Перевірка гіпотези про рівність часток ознаки двох сукупностей

Задача порівняння часток (відносних частот) ознаки в двох сукупностях досить часто зустрічається на практиці. Наприклад, якщо вибіркова частка ознаки однієї сукупності відрізняється від такої ж частки в другій сукупності, чи вказує це на те, що наявність ознаки в одній сукупності дійсно ймовірніше, чи ця різниця часток є випадковою?

Сформулюємо задачу. Маємо дві сукупності, генеральні частки ознаки яких дорівнюють відповідно р₁ і р₂. Необхідно перевірити нульову гіпотезу про рівність генеральних часток, тобто Н₀: р₁=р₂ . Для перевірки гіпотези Н₀ із цих сукупностей взяті дві незалежні вибірки достатньо великого об’єму п₁ і п₂. Вибіркові частки ознаки рівні відповідно і, дет₁ і т₂ – відповідне число елементів першої і другої вибірки, що має дану ознаку.

При достатньо великих п₁ і п₂, вибіркові частки імають наближено нормальний закон розподілу з математичним сподіваннямр₁ і р₂ і дисперсіями і, тобто відповідноN(р₁; ) іN(р₂; ).

При справедливості гіпотези Н₀: р₁=р₂=р різниця -має нормальний закон розподілу з математичним сподіванням М(‑)=р‑р=0 і дисперсією .Тому статистика

має стандартний нормальний розподіл N(0;1)

В якості невідомого значення р що входить у вираз статистики t, беруть його найкращу оцінку , рівну вибірковій частці ознаки, якщо дві вибірки з’єднати в одну, тобто.

Вибір виду критичної області і перевірка гіпотези здійснюється таким же чином, як і вище, при перевірці гіпотези про рівність середніх.

Приклад. Контрольну роботу з математичної статистики по індивідуальним варіантам виконували студенти двох груп першого курсу. В першій групі було запропоновано 105 задач, з яких правильно розв’язано 60, у другій із 140 запропонованих правильно розв’язано 69. На рівні значимості 0,02 потрібно перевірити гіпотезу про відсутність суттєвої різниці в засвоєнні навчального матеріалу студентами обох груп.

Розв’язання

Припустимо, що частки розв’язаних задач студентами обох груп рівні, тобто Н₀: р₁=р₂= р. В якості альтернативної візьмемо гіпотезу Н₁: р₁р₂. При справедливості гіпотези Н₀ найкращою оцінкою р буде

=. Вибіркові частки розв’язаних задач для кожної групиі. Статистику критерію обчислимо за формулою:

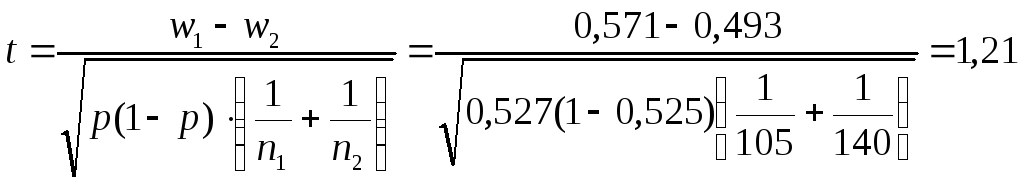
При конкуруючій гіпотезі Н₁: р₁р₂ обираємо критичну двосторонню область: Ф(t_кр)=1-0,02=0,98, звідки за таблицею значень функції Лапласа t_кр= t_0,98=2,33. Фактичне значення критерію менше критичного, тобто tt_0.98 . Отже, гіпотеза Н₀ приймається, тобто отримані дані не протирічать гіпотезі про однаковий рівень засвоєння навчального матеріалу студентами обох груп.

0. Перевірка гіпотези про рівність дисперсій двох сукупностей

Гіпотези про дисперсії виникають доволі часто, оскільки дисперсія характеризує такі виключно важливі показники, як точність машини, приладу, технологічних процесів, ступінь однорідностей сукупностей і т.і.

Сформулюємо задачу. Нехай маємо дві нормально розподілені сукупності, дисперсії яких рівні і. Необхідно перевірити нульову гіпотезу про рівність дисперсій, відносно конкурентної Н₁: >або Н₂:  .

Для перевірки гіпотези Н₀із цих сукупностей взяли дві незалежні вибірки об’ємами п₁ і п₂. Для оцінки дисперсій івикористаємо виправлені вибіркові дисперсіїі. Звідси, задача перевірки гіпотези зводиться до порівняння дисперсійі.

Доведено, що випадкова величина F, що визначається відношенням:

₍₃₂₎

_{має F- розподіл Фішера-Снедекора з k1=n1-1 і k2=n2-1 ступенями вільності.}

Слід мати на увазі, що F-розподіл Фішера-Снедекора є несиметричним, тому гіпотеза Н₀ відхиляється, якщо F>F_,k1;k2 (у випадку правосторонньої критичної області) або FF_{1-/2,k1;k2} чи F>F_/2,k1;k2 (у випадку двосторонньої критичної області). У протилежному випадку гіпотеза Н₀ приймається.

Приклад. На двох токарних станках обробляються деталі. Відібрані дві проби: із деталей, зроблених на першому станку, п₁=15шт., на другому п₂=18шт. Поданих цих вибірок розраховані вибіркові дисперсії івідповідно. Припускаючи, що розміри деталей підпорядковуються нормальному закону розподілу, на рівні значимості=0,05 з’ясувати, чи можна вважати, станки володіють різною точністю.

Розв’язання

Припустимо, що дисперсії розмірів деталей, що оброблялися кожним станком рівні, тобто Н₀: =. Тоді Н₁: >(дисперсія першого більша).

За формулою (32) маємо (в якості дисперсіїберуть більшу із двох дисперсій).

За таблицею критичних значень F-Фішера (додаток 6) при рівні значимості =0,05 та k₁=п₁-1=14 і k₂=п₂-1=17 знаходимо критичне значення, тобто F_кр=F_{0,05; 14;17}=2,33. Оскільки F F_кр, то гіпотеза Н₀ не відхиляється.

Зауваження. Якщо Н₁:  , то слід знайтиF_{1-/2;k1;k2} і F_/2;k1;k2, Оскільки за таблицею можна знайти лише праву границю, то ліву знаходять із співвідношення, доведеного для F-критерію: F_{1‑/2;k1;k2}=. У даному випадку при=0,05 в задачі потрібно знайти F_0,025;14;17 і F_0,975;14;17=.

Приклад . За рівнем значущості =0,05 порівняти вагу семимісячних немовлят двох груп (перша група мала штучне вигодовування, а друга – грудне), якщо за вибірками одержали такі показники

п₁=20; =8,0; S_x=0,3

п₂=25; =8,6;S_у=0,4

Розв’язання

За рівнем значущості =0,05 перевіримо гіпотезу про рівність середніх Н₀: =, при альтернативній гіпотезі Н₁: .

Спочатку перевіримо гіпотезу про рівність дисперсій : ²_х=²_у при альтернативній гіпотезі : ²_х ²_у .

Обчислимо значення критерію за формулою (32) _.

_{За таблицею критичних значень розподілу Фішера (додаток 6) для} =0,05 і кількості ступенів вільності к₁=25-1=24, к₂=20-1=19, знаходимо критичну точку F_кр. =2,11.

Оскільки F  F_кр. , то :²_х=²_у приймаємо і нема підстав відхиляти гіпотезу про рівність середніх.

Обчислимо спостережуване значення статистики за формулою (31):

_t=

За таблицею критичних значень розподілу Стьюдента (додаток 5) для =0,05 і кількості ступенів вільності к=20+25-2=43 знаходимо критичну точку розподілу Стьюдента t_кр. =2,02.

Оскільки tt_кр., то гіпотезу про рівність середніх відхиляємо. Тобто середня вага немовлят, що росли на штучному харчуванні менша ніж середня вага немовлят, що вигодовувалися грудним молоком.

0. Перевірка гіпотез про числові значення параметрів

Нехай х_і (і=1,2,...,п) – значення деякого параметра виробу, що виготовляється станком автоматичної лінії, і нехай а – задане номінальне значення цього параметру. Кожне окреме значення х_і може, очевидно, якось відхилятися від заданого номіналу. Очевидно, для того, щоб перевірити правильність налаштування цього станка, потрібно переконатися в тому, що середнє значення параметра у виготовлених на ньому виробів буде відповідати номіналу. Що означає перевірити гіпотезу Н₀:при альтернативній Н₁:, або Н₂:а, або Н₃:>а.

При довільному на лаштуванні станка може виникнути необхідність перевірки гіпотези про те, що точність виготовлення виробів по даному параметру, що задана дисперсією , рівна заданій величині, тобто Н₀: =, або наприклад, що частка бракованих виробів, що виготовляються станком, рівна заданій величинір₀, тобто Н₀:р= р₀.

Відповідні критерії перевірки гіпотез про числові значення параметрів нормального закону приведені в таблиці

Нульова гіпотеза	Припущення	Статистика критерію	Альтернативна гіпотеза	Критерій відхилення гіпотези
	відоме
	невідоме
	а невідоме			або
	Достатньо великі п