Запитання для самоконтролю

1. Що таке статистична гіпотеза? Які є види статистичних гіпотез? Навести приклади статистичних гіпотез.

2. В чому полягають помилки першого та другого роду, які виникають при перевірці гіпотез?

3. Що називають статистичним критерієм перевірки гіпотез? Що таке потужність критерію?

4. Що таке критична область, як її знайти?

5. Яка статистика критерію використовується для перевірки гіпотези про закон розподілу випадкової величини? За якою формулою її обчислюють?

6. Яка статистика критерію використовується для перевірки гіпотези про рівність середніх двох сукупностей? За якою формулою її обчислюють?

7. Яка статистика критерію використовується для перевірки гіпотези про рівність дисперсій двох сукупностей? За якою формулою її обчислюють?

8. Яка статистика критерію використовується для перевірки гіпотези про рівність часток ознаки двох сукупностей? За якою формулою її обчислюють?

9. Що означає перевірити гіпотезу про числові значення параметрів? Навести приклад таких гіпотез?

Тема 10. Елементи теорії кореляції

Кореляційний аналіз досліджує наявність і характер зв’язків між випадковими величинами ознаками генеральної сукупності.

Основна задача кореляційного аналізу полягає у виявленні залежності між випадковими величинами Х та У і може бути розв’язана шляхом побудови статистичних оцінок коефіцієнта кореляції.

Точкову оцінку для коефіцієнта кореляції обчислюють за формулою:

(33)

Означення. Точкова оцінка коефіцієнта кореляції між випадковими величинами Х та У. яка обчислюється за формулою (33), називаєтьсявибірковим коефіцієнтом кореляції.

Вибірковий коефіцієнт кореляції характеризує зв’язок між випадковими величинами Х ті У (ознаками генеральної сукупності):

а) якщо 0, то зв’язок між Х та У є прямий і вони зменшуються або збільшуються одночасно;

б) якщо 0, то зв’язок між Х та У є обернений і із збільшенням однієї з них друга зменшується або навпаки;

в) ) якщо =0, то випадкові величини Х та У є некорельовані і це означає лише відсутність лінійного зв’язку між ними.

Вибірковий коефіцієнт кореляції задовольняє нерівність ≤1.

Нехай потрібно встановити залежність між двома випадковими величинами Х та У. Ці дві випадкові величини можуть бути зв’язані або функціональною залежністю, або так званою статистичною залежністю, або бути незалежними.

Строга функціональна залежність реалізується рідко.

Означення. Статистичною називається залежність, при якій зміна однієї величини викликає зміну розподілу іншої.

Означення. Кореляційною називається статистична залежність, яка проявляється в тому, що при зміні однієї величини змінюється середнє значення іншої.

Причому при кореляційній залежності одному значенню незалежної змінної Х відповідає не одне, а декілька значень залежної змінної У.

Приклад. Нехай Х – випадкова величина, що характеризує вагу людини в кг, а У – відповідний зріст в см і двовимірний статистичний розподіл задається такою таблицею

У	Х
	70	75	80	п
170	15	10	5	30
175	–	10	–	10
180	–	5	5	10
п	15	25	10	50

Число, яке лежить на перетині стовпчика х_і і рядка у_і , вказує частоту, з якою зустрічається пара чисел (х_і; у_і).

Умовною середньою називається середнє арифметичне із значень У, що відповідають одному і тому ж значенню Х=х.

Так, вазі 75 кг відповідає середній зріст

.

Аналогічно знаходиться умовна середня .Очевидно, що умовна середня є функцією х, у цьому випадку говорять, що величина У залежить від Х кореляційно. Використовуючи поняття умовної середньої, введемо таке означення кореляційної залежності.

Означення. Кореляційною називається залежність умовної середньої від аргументів х:=.

Якщо є дві і більш змінних то: =.

Рівняння =називаютьрівнянням регресії У на Х, функцію називають регресією У на Х, а її графік – лінією регресії.

Найпростішою буде кореляційна залежність, коли є один аргумент. Її називають парною.

Якщо аргументів більше ніж один, то залежність називається множинною.

Вигляд рівняння визначає тип кореляційної залежності.

Найбільш поширеним є рівняння лінійної регресії =та та квадратичної=. Відповідно лінії регресії зображені на рис. 8.

у

у

х₁ х₂ х₃ х_n х

х₁ х₂ х₃ х_n х

y=ax+b y=ax²

Рис. 8

Неважко довести, що коефіцієнти рівняння регресії =є розв’язками системи рівнянь 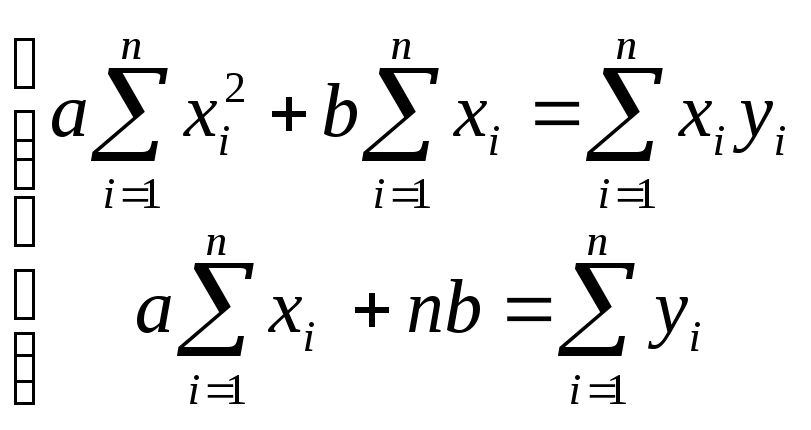і дорівнюють

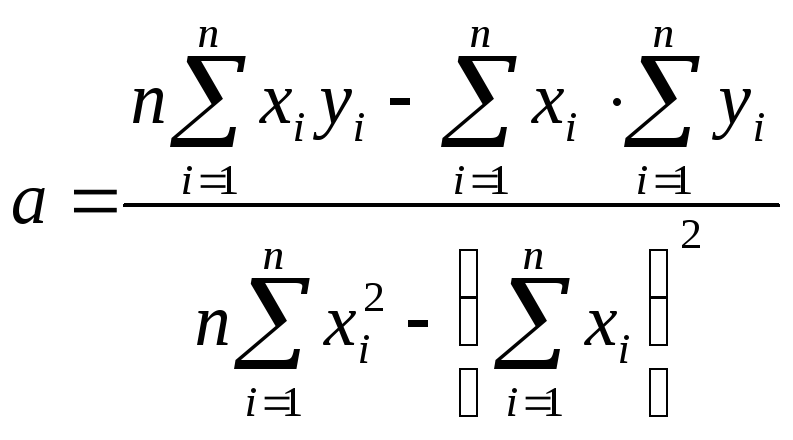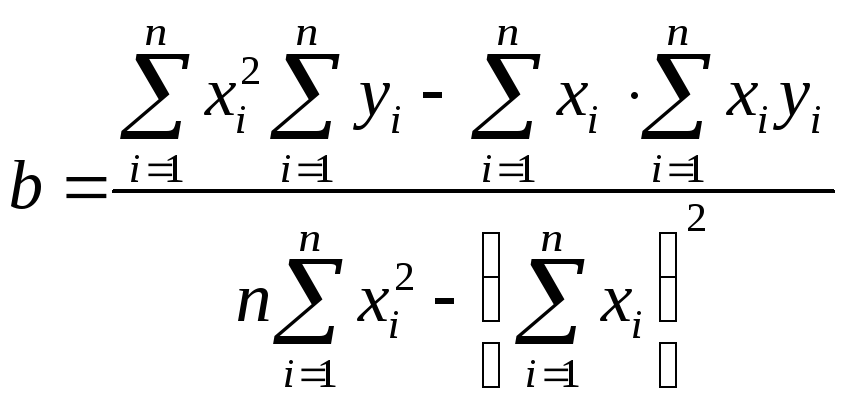та (34)

А коефіцієнти рівняння є розв’язком системи рівнянь

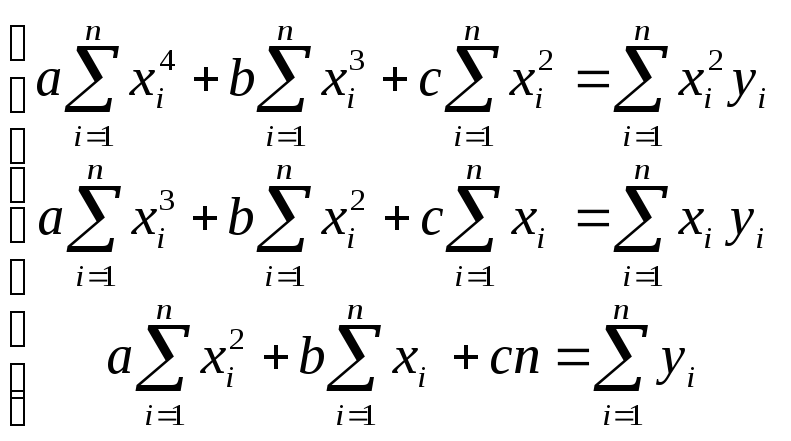і дорівнюють

,,

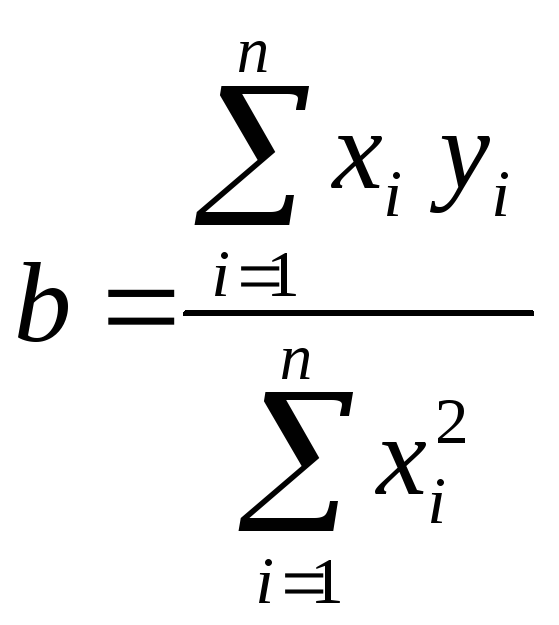Для знаходження вибіркового рівняння регресії У на Х за даними спостережень використовують метод "натягнутої нитки", методом сум та метод найменших квадратів.

Приклад. Знайти вибіркове рівняння регресії У на Х за даними спостережень: а) методом "натягнутої нитки", б) методом сум, в) методом найменших квадратів. Обчислити коефіцієнт кореляції та дати його тлумачення.

Х	30	28	26	31	15	20	23	27	28	22	21	23	26	30	31	25	25	27	28	23
У	47	45	41	49	25	33	37	43	46	35	35	37	42	47	49	40	39	43	45	37

Розв’язання

а) метод "натягнутої нитки"

Будуємо кореляційне поле за вибіркою (Х;У):

Через точки кореляційного поля проводимо пряму так, щоб в обох півплощинах знаходилася приблизно однакова кількість точок. На цій прямій обираємо дві точки. Наприклад, А(15,25) і В(30,47). Складаємо систему для визначення коефіцієнтів лінійного рівняння залежності між Х та У: y=ax+b. Система буде такою:

.

Отже, рівняння має вигляд: у=1,47х+3

б) метод сум

Умовно ділимо вибірку на дві рівні частини (по 10 елементів). Тоді визначальна система для коефіцієнтів а та b буде такою:

Обчислимо всі суми, які присутні в системі. Розрахунки заносимо в таблицю:

	X	Y	XY	X^2	Y^2
	30	47	1410	900	2209
	28	45	1260	784	2025
	26	41	1066	676	1681
	31	49	1519	961	2401
	15	25	375	225	625
	20	33	660	400	1089
	23	37	851	529	1369
	27	43	1161	729	1849
	28	46	1288	784	2116
	22	35	770	484	1225
Сума	250	401
	21	35	735	441	1225
	23	37	851	529	1369
	26	42	1092	676	1764
	30	47	1410	900	2209
	31	49	1519	961	2401
	25	40	1000	625	1600
	25	39	975	625	1521
	27	43	1161	729	1849
	28	45	1260	784	2025
	23	37	851	529	1369
Сума	259	414
Загальна сума	509	815	21214	13271	33921

Тоді система набуває вигляду:

.

Відповідне рівняння у=1,6х+0,1.

в) метод найменших квадратів

Визначальна система для коефіцієнтів рівняння така:

Відповідне рівняння у=1,49х+2,83.

Коефіцієнт кореляції обчислюємо за формулою:

Проміжні обчислення:

; ;

,

Тоді .

Оскільки коефіцієнт кореляції дуже близький до 1, то залежність між Х та У можна вважати лінійною.

Приклад. Зв’язок між кількісними ознаками Х та У генеральної сукупності задається таблицею

Х	2	3	4	5	6	7	8	9	10	11
У	1	5	7	11	13	17	19	23	25	29

Записати рівняння прямої регресії У на Х.

Розв’язання

Скористаємося формулами (34) для знаходження коефіцієнтів лінійної регресії. отримаємо а=3,03, b=-4,70.

Отже вибіркове рівняння регресії: у=3,03х-4,7.

Щоб переконатися в тому, що наше припущення про лінійність зв’язку між Х та У було правильним, обчислимо вибірковий коефіцієнт кореляції за формулою (33), отримаємо

Оскільки вибірковий коефіцієнт кореляції є досить близьким до одиниці, то припущення про лінійність зв’язку між Х та У – правильне. Крім цього, зв’язок є додатний і ці величини збільшуються одночасно.