
- •Лекция 1. Основные понятия и определения
- •1. Люди, принимающие решения
- •2. Люди и их роли в процессе принятия решений
- •3. Особая важность проблем индивидуального выбора
- •4. Альтернативы
- •5. Критерии
- •6. Оценки по критериям
- •7. Процесс принятия решений
- •8. Множество Эджворта-Парето
- •9. Типовые задачи принятия решений
- •10. Пример согласования интересов лпр и активных групп
- •11. Многодисциплинарный характер науки о принятии решений
- •Лекция 2. Аксиоматические теории рационального поведения
- •1. Рациональный выбор в экономике
- •2. Аксиомы рационального поведения
- •3. Задачи с вазами
- •4. Деревья решений
- •5. Парадокс Алле
- •6. Нерациональное поведение. Эвристики и смещения
- •7. Объяснения отклонений от рационального поведения
- •8. Должны ли экономисты принимать во внимание отклонения поведения людей от рационального?
- •9. Теория проспектов
- •10. Теория проспектов и парадокс Алле
- •11. Новые парадоксы
- •Волшебные страны Компьютерная игра в Университете Власти
- •Лекция 3. Многокритериальные решения при объективных моделях
- •1. Модели
- •2. Подход исследования операций
- •3. Появление многокритериальное
- •4. Первые многокритериальные решения: сколько строить ракет?
- •5. Разные типы проблем
- •6. Два пространства
- •7. Многокритериальный анализ экономической политики
- •8. Две трудности для лпр
- •9. Исследование решений на множестве э-п
- •10. Постановка многокритериальной задачи линейного программирования
- •11. Человекомашинные процедуры
- •12. Весовые коэффициенты важности критериев
- •13. Классификация чмп
- •14. Прямые человекомашинные процедуры
- •15. Процедуры оценки векторов
- •16. Процедуры поиска удовлетворительных значений критериев
- •Фаза расчетов
- •Фаза анализа
- •17. Пример применения метода stem : как управлять персоналом
- •Волшебные страны Обращение ректора Университета Власти к студентам
- •Лекция 4. Оценка многокритериальных альтернатив: многокритериальная теория полезности
- •1. Снова об этапах процесса принятия решений
- •2. Различные группы задач принятия решений
- •Задачи первой группы
- •Задачи второй группы
- •3. Пример
- •4. Многокритериальная теория полезности ( maut )
- •4.1. Основные этапы подхода maut
- •4.2. Аксиоматическое обоснование
- •4.3. Основные теоремы
- •4.4. Построение однокритериальных функций полезности
- •4.5. Проверка условий независимости
- •4.6. Определение весовых коэффициентов (коэффициентов важности) критериев
- •4.7. Определение полезности альтернатив
- •5. Метод smart – простой метод многокритериальной оценки
- •6. Первый эвристический метод
- •7. Веса критериев
- •8. Как люди назначают веса критериев
- •9. Практическое применение
- •Библиографический список
- •Волшебные страны Компьютерная генетика
- •Лекция 5. Оценка многокритериальных альтернатив: подход аналитической иерархии
- •1. Основные этапы подхода аналитической иерархии
- •2. Структуризация
- •3. Попарные сравнения
- •4. Вычисление коэффициентов важности
- •5. Определение наилучшей альтернативы
- •6. Проверка согласованности суждений лпр
- •7. Система поддержки принятия решений Expert Choice
- •8. Контрпримеры и противоречия
- •9. Мультипликативный метод аналитической иерархии
- •10. Пример практического применения подхода анр
- •Библиографический список
- •Лекция 6.Оценка многокритериальных альтернатив: методыelectre
- •1. Конструктивистский подход
- •2. Два основных этапа
- •3. Свойства бинарных отношений
- •4. Метод electre I
- •5. Метод electre II
- •6. Метод electre III
- •7. Пример
- •8. Пример практического применения метода electre III
- •9. Некоторые сопоставления
- •Модель человеческого мозга «Грандом», созданная в Монтландии
- •Лекция 7. Человеческая система переработки информации и ее связь с принятием решений
- •1. Этапы переработки информации, типы памяти
- •2. Модель памяти
- •3. Кратковременная память
- •3.1. Три этапа переработки информации в кратковременной памяти
- •3.2. Кодирование
- •3.3. Хранение
- •3.4. Магическое число
- •3.5. Денежный насос
- •3.6. Последовательная обработка информации
- •3.7. Извлечение
- •4. Дескриптивные исследования многокритериальных проблем
- •4.1. Прослеживание процесса принятия решений
- •4.2. Результаты дескриптивных исследований
- •5. Долговременная память
- •5.1. Кодирование
- •5.2. Хранение
- •5.3. Извлечение
- •6. Рабочая память
- •7. Психологические теории человеческого поведения при принятии решений
- •7.1. Теория поиска доминантной структуры
- •7.2. Теория конструирования стратегий
- •8. Исследование возможностей человека в задачах классификации многомерных объектов
- •8.1. Схема экспериментов
- •8.2. Параметры, используемые для оценки поведения испытуемых в задачах классификации
- •8.3. Описание экспериментов
- •8.4. Результаты экспериментов
- •8.5. Обсуждение результатов первой серии экспериментов
- •8.6. Анализ и обсуждение результатов второй серии экспериментов
- •8.7. Общее обсуждение
- •Библиографический список
- •История бюрократии в Монтландии
- •Лекция 8. Оценка многокритериальных альтернатив: вербальный анализ решений
- •1. Особый класс задач принятия решений: неструктурированные проблемы с качественными переменными
- •2. Качественная модель лица , принимающего решения
- •2.1. Черты человеческой системы переработки информации
- •2.2 Особенности поведения человека при принятии решений
- •3. Какими должны быть методы анализа неструктурированных проблем
- •4. Измерения
- •4.1. Качественные измерения
- •4.2. Сравнительные качественные оценки
- •5. Построение решающего правила
- •6. Проверка информации лпр на непротиворечивость
- •7. Обучающие процедуры
- •8. Получение объяснений
- •9. Основные характеристики методов вербального анализа решений
- •10. Метод запрос ( Замкнутые Процедуры у Опорных Ситуаций )
- •10.1. Постановка задачи
- •10. 2. Пример : как оценить проекты ?
- •10.3. Выявление предпочтений лпр
- •10.4. Сравнение альтернатив
- •10.5. Преимущества метода запрос
- •10.6. Практическое применение метода запрос
- •11. Сравнение трех сппр
- •Библиографический список
- •Контрольное задание
- •Компьютерные двойники
- •Лекция 9. Повторяющиеся решения. Построение баз экспертных знаний
- •1. Процесс мышления как манипулирование символами
- •2. Два типа знания
- •3. Время и условия становления эксперта
- •4. Трансформация системы переработки информации
- •5. Иерархические структуры хранения знаний
- •6. Черты поведения эксперта
- •7. Подсознательный характер экспертных знаний
- •8. Трудности получения экспертных знаний
- •9. Экспертные знания в задачах классификации с явными признаками
- •10. Формальная постановка задачи классификации
- •11. Основные идеи метода экспертной классификации
- •11.1. Структуризация проблем
- •11.2. Классификация состояний объекта исследования
- •11.3. Гипотеза о характерности
- •11.4. Проверка информации эксперта и гипотезы о характерности
- •11.5. Определение последовательности состояний для предъявления эксперту в процессе классификации
- •11.6. Трудоемкость построения баз знаний
- •11.7. Проверка качества баз знаний
- •12. Граничные элементы классификации
- •13. Решающие правила экспертов
- •14. Система диагностики заболеваний группы
- •Библиографический список
- •Лекция 10. Анализ риска
- •1. Типы риска
- •2. Особая сложность задач анализа риска
- •3. Направления исследований
- •4. Измерение риска
- •4.1. Инженерный подход
- •4.2. Модельный подход
- •4.3. Восприятие риска
- •4.4. Сопоставление разных способов измерения риска
- •5. Установление стандартов
- •6. Человекомашинное взаимодействие
- •7. Риск катастрофических событий как независимый критерий
- •8. Распределения "с тяжелыми хвостами"”
- •9. Аварии и их анализ
- •10. Управление риском
- •11. Практический пример: выбор месторасположения нового объекта с учетом факторов риска
- •11.1. Конкретная задача: альтернативы
- •11.2. Активные группы
- •11.3. Критерии
- •11.4. Особенности задачи выбора с точки зрения теории принятия решений
- •11.5. Анализ вариантов
- •11.6. Конструирование нового варианта
- •Библиографический список
- •Контрольное задание
- •Волшебные страны Компьютерная демократия Монтландии
- •Лекция 11. Коллективные решения
- •1. Парадокс Кондорсе
- •2. Правило большинства голосов
- •3. Метод Борда
- •4. Аксиомы Эрроу
- •5. Попытки пересмотра аксиом
- •6. Теорема невозможности и реальная жизнь
- •7. Принятие коллективных решений в малых группах
- •8. Организация и проведение конференций по принятию решений
- •9. Метод организации работы гпр
- •9.1. Предварительные этапы
- •9.2. Анализ собранной информации
- •9.3. Проведение конференции по принятию решений
- •9.4. Практический пример
- •Библиографический список
- •Волшебные страны Военный переворот в Свапландии ( Статья в оппозиционной газете «Вечерний наблюдатель» , выходящей в столице Монтландии - Олоне).
- •К событиям в Свапландии ( Статья в правительственной газете «Олон - пост» , выходящей в столице Монтландии - Олоне .)
- •Лекция 12. Многокритериальная задача о назначениях
- •1. Определение и особенности
- •2. Постановка многокритериальной задачи о назначениях
- •2.1. Содержательная постановка задачи
- •2.2. Критерий оптимальности решения мзн
- •2.3. Формальная постановка задачи
- •3. Пример
- •4. Различные типы задач о назначениях
- •5. Основные алгоритмы решения многокритериальной задачи о назначениях
- •5.1. Различные индексы соответствия
- •5.2. Поиск решения многокритериальной задачи о назначениях
- •6. Этап анализа данных и проверки существования идеального решения
- •7. Формирование области допустимых решений
- •8. Выявление предпочтений лпр
- •8.1. Статистические оценки сложности задач выявления предпочтений лпр
- •8.2. Основная процедура выявления предпочтений лпр
- •8.3. Выявление предпочтений лпр ; вспомогательная процедура
- •9. Поиск окончательного решения многокритериальной задачи о назначениях
- •9.1. Поиск решения мзн типа а
- •9.2. Поиск решения мзн типа в
- •9.3. Поиск решения мзн типа с
- •9.4. Поиск решения мзн типа d
- •10. Практическое применение
- •Библиографический список
- •Контрольное задание
- •Волшебные страны Стратегия правления в Свапландии (Статья в Правительственной газете «Олон-пост», выходящей в столице Монтландии - Олоне.)
- •Прыжок в никуда
- •Лекция 13 принятие решений в организациях
- •1. Личные и деловые решения
- •2. Модель ограниченной рациональности
- •3. Эскалация решений
- •4. Тактические и стратегические решения
- •5. Модель «игра влияний» в руководстве организации
- •6. Модель обеспечения профессионального качества подготовки решений
- •7. Топографическая модель организации
- •8. Государственные или частные организации: что эффективнее?
- •9. Централизация в принятии решений: попытка административной революции
- •10. Система «ринго»
- •11. Планирование выполнения решений
- •12. Виртуальные организации
- •13. Управление знаниями в организациях
- •14. Метод милс (Многоуровневые Информационно-Логические Структуры)
- •15. Таблицы решений
3. Задачи с вазами
Теория полезности экспериментально исследовалась в так называемых задачах с вазами (или урнами). Ваза - это непрозрачный сосуд, в котором находится определенное (известное лишь организатору эксперимента) количество шаров различно го цвета. Задачи с вазами типичны для группы наиболее простых задач принятия решений — задач статистического типа. Для решения этих задач надо знать элементарные начала тео рии вероятностей [4]. Человек делает выбор в этих задачах, основываясь на расчетах. Варианты действий выражены в наибо лее простом виде.
Типовая задача для испытуемого может быть представлена следующим образом [3]. Перед испытуемым ставится ваза, ко торая может быть вазой 1-го или 2-го типа. Дается следующая информация: сколько имеется у экспериментатора ваз 1-го и 2-го типов; сколько черных и красных шаров в вазах 1-го и 2-го типов; какие выигрыши ожидают испытуемого, если он угадает, какого типа ваза; какие проигрыши ожидают его, если он ошибется. После получения такой информации испытуемый должен сделать выбор: назвать, к какому типу принадлежит поставленная перед ним ваза.
Пусть, например, экспериментатор случайно выбирает вазу для испытуемого из множества, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа. Если перед испытуемым находится ваза 1-го типа и он угадает это, то получит выигрыш 350 денежных единиц (д.е.), если не угадает, его проигрыш составит 50 д.е. Если перед ним ваза 2-го типа и он это угадает, то получит вы игрыш 500 д.е., если не угадает, его проигрыш составит 100 д.е. Примем, что полезность для испытуемого равна каче ству денежных единиц. Испытуемый может предпринять одно из следующих действий: d 1 - сказать, что ваза 1-го типа; d 2 —сказать, что ваза 2-го типа.
Условия задачи можно представить в табл. 2.1.
Таблица 2.1. Представление задачи с вазами
|
Тип вазы |
Вероятность выбора вазы данного типа |
Действия и выигрыши | |
|
d 1 |
d 2 | ||
|
1 |
0.7 |
350 |
-100 |
|
2 |
0.3 |
-50 |
500 |
Что же делать человеку? Теория полезности отвечает: оценить среднюю (ожидаемую) полезность каждого из действий и выбрать действие с максимальной ожидаемой полезностью. В соответствии с этой рекомендацией мы можем определить среднее значение выигрыша для каждого из действий:
U ( d 1 ) = 0,7 xor 350 - 0,3 xor 50 = 230 д.е;
U ( d 2 ) = 0,3 xor 500 - 0,7 xor 100 = 80 д.е.
Следовательно, разумный человек выберет действие d 1 а не действие d 2 .
Из этого примера следует общий рецепт действий для ра ционального человека: определить исходы, помножить их на соответствующие вероятности, получить ожидаемую полезность и выбрать действие с наибольшей полезностью.
Задачи с вазами помогут нам познакомиться с построением деревьев решений и принятием решений с их помощью.
4. Деревья решений
Приведенная выше табл. 2.1 может быть представлена в виде дерева решений (рис. 2.3). На этом дереве квадратик озна чает место, где решение принимает человек, а светлый кру жок - место, где все решает случай. На ветвях дерева написа ны уже знакомые нам значения вероятностей, а справа у конеч ных ветвей - значения исходов (результаты).
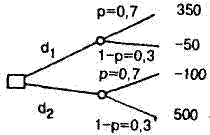
Рис. 2.3. Дерево решений
Для чего нужно дерево решений? Мы можем использовать его для представления своих возможных действий и для нахо ждения последовательности правильных решений, ведущих к максимальной ожидаемой полезности. Чтобы показать это, ус ложним задачу. Пусть в вазе 1-го типа содержится 6 красных и 4 черных шара. В вазе второго типа содержится 3 красных и 7 черных шаров. Предоставим человеку, выбирающему между действиями d 1 и d 2 , дополнительные возможности. Пусть он может до своего ответа вытащить за определенную плату один шар из вазы, причем после вытаскивания шар кладется обратно в вазу. Плата за вытаскивание одного шара равна 60 д. е.
Дерево решений с двумя его основными ветвями представ лено на рис. 2.4. Вот теперь вопрос о том, какое решение сле дует принимать, стал сложнее: необходимо решить, стоит ли вынимать шар и какой ответ дать после вытаскивания красно го или черного шара. При принятии этих решений нам окажет существенную помощь известный в теории вероятностей [4] (и в теории статистических решений) способ подсчета изменения вероятностей событий после получения дополнительной ин формации.
Вернемся к описанию задачи. Вероятность вытащить крас ный шар из вазы 1-го типа p K ( B 1 )=0,6, а из вазы 2-го типа p к (В 2 )=0,3. Зная все условные вероятности (зависящие от усло вия), а также вероятности p 1 и p 2 выбора ваз 1-го и 2-го типа (см. табл. 2.1), мы можем поставить следующие вопросы.
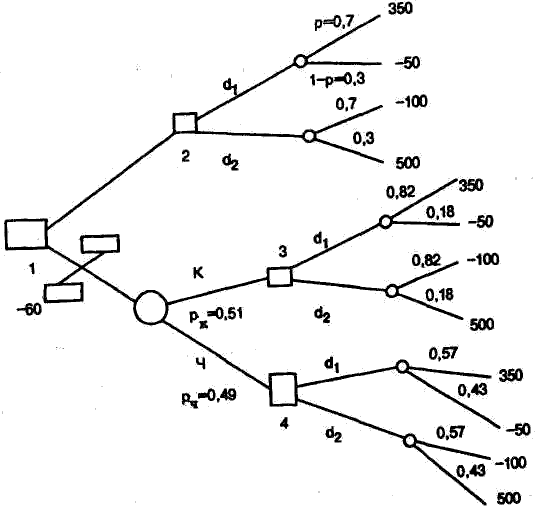
Рис. 2.4. Дерево решений
Первый вопрос: каковы вероятности вытащить красный и черный шары? Для ответа на этот вопрос произведем простые вычисления. Вероятность вытащить красный шар: p K ( B 1 )=0,7 A 0,6=0,42, если ваза окажется 1-го типа, p к (В 2 )=0,3 A 0,3=0,09, если ваза окажется 2-го типа. Следовательно, вероятность вы тащить красный шар в общем случае р к =0,51. Аналогичным образом можно посчитать, что вероятность вытащить черный шар Рч=0,49.
Второй вопрос более сложный. Пусть вытащенный шар оказался красным (черным). Какое действие следует выбрать: d 1 или d 2 ? Для ответа на этот вопрос нужно знать вероятности принадлежности ваз к 1-му и 2-му типам после получения до полнительной информации. Эти вероятности позволяет опреде лить знаменитая формула Байеса [4].
Например, мы вытащили красный шар. Какова после этого вероятность того, что перед нами стоит ваза 1-го типа?
Приведем все обозначения вероятностей:
p k ( B 1 ) - вероятность вытащить красный шар из вазы 1-го типа;
p ч ( B 1 ) — вероятность вытащить черный шар из вазы 1-го типа;
p к(В 2 ) ~ вероятность вытащить красный шар из вазы 2-го типа;
p ч (В 2 ) — вероятность вытащить черный шар из вазы 2-го типа;
p ( B 1 ) - вероятность того, что ваза окажется 1-го типа;
р(В 2 ) - вероятность того, что ваза окажется 2-го типа;
p ( B 1/ K ) - вероятность того, что ваза окажется 1-го типа по сле вытаскивания красного шара;
p ( B 1/ч ) - вероятность того, что ваза окажется 1-го типа после вытаскивания черного шара;
р(В 2/к ) - вероятность того, что ваза окажется 2-го типа по сле вытаскивания красного шара;
p (В 2/ч ) - вероятность того, что ваза окажется 2-го типа по сле вытаскивания черного шара.
Формула Байеса позволяет оценить p ( B i / K ) и p ( B i /ч ), где i =1, 2, используя все прочие вероятности. Например:

Для нашей задачи: p ( B 1/ K )=0,82; p ( B 1/ч )=0,57; p ( B 2/ K )=0,18; р(В 2/ч )=0,43.
Теперь мы имеем всю информацию, необходимую для при нятия решений.
На рис. 2.4 показаны две основные ветви дерева решений, причем верхняя просто повторяет дерево решений на рис. 2.3. Квадратик 1 слева соответствует первому решению - вытаски вать шар или нет. Случаю отказа от вытаскивания шара соот ветствует верхняя основная ветвь. Решению вытаскивать шар соответствует нижняя ветвь, начинающаяся со случайного со бытия (кружок). В квадратиках 2, 3, 4 принимаются решения о выборе одной из двух стратегий: d 1 или d 2 . Далее все решает случай (кружки).
Есть три простых правила выбора оптимальной (по крите-, рию максимума ожидаемой полезности) последовательности ре-шений на основе дерева решений:
• идти от конечных ветвей дерева к его корню;
• там, где есть случайность (кружок), находится среднее значение;
• там, где есть этап принятия решений (квадратик), выбирается ветвь с наибольшей ожидаемой полезностью, а другая отсекается двумя черточками.
Применим эти правила к дереву решений, представленному на рис. 2.4. В результате получим дерево решений, показанное на рис. 2.5.
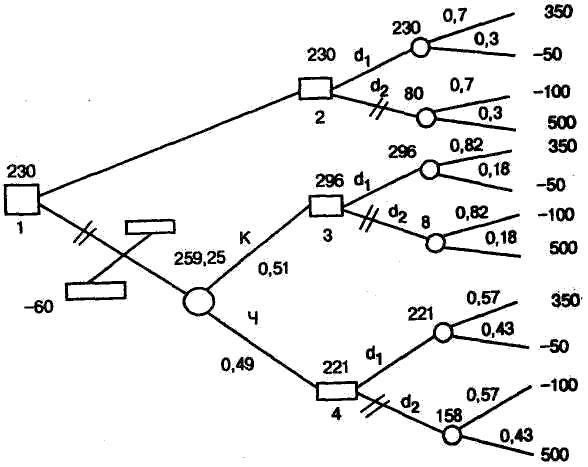
Рис. 2.5. «Сворачивание» дерева решений
На этом рисунке над кружками указаны средние значения полезности, двумя черточками отсечены ветви с меньшим значением ожидаемой полезности. Наилучший вариант действий: шар не вытаскивать и выбирать действие d 1 . Этот вариант соот ветствует самому верхнему пути дерева решений на рис. 2.5. Такая процедура нахождения оптимального пути на деревьях решений получила название «сворачивание» дерева решений.
Деревья решений при заданных числовых значениях веро ятностей и исходов позволяют осуществить выбор той страте гии (последовательности действий), при которой достигается наибольший выигрыш, т.е. достигается максимум функции по лезности ЛПР.
