Задача 4.1

Для нахождения дисперсии группы показателей (1,3,3,0,4,7) удобно вычисления оформить в виде таблицы 4.1.

Таблица 4.1

1	-2	4
3	0	0
3	0	0
0	-3	9
4	1	1
7	4	16
Сумма	0	30

При значение выборочной дисперсии находится по формуле (4.2):

.

Важная характеристика дисперсии заключается в том, что с ее помощью можно сравнивать выборки, различные по объему.

Однако сама дисперсия, как характеристика отклонения от среднего, часто неудобна для интерпретации. Так, например, предположим, что в эксперименте измерялся рост в сантиметрах, тогда размерность дисперсии будет являться характеристикой площади, а не линейного размера.

Для того чтобы приблизить размерность дисперсии к размерности измеряемого признака, применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют выборочным стандартным отклонением:

. (4.3)

Формулы (4.2) и (4.3) предназначены для вычисления статистик выборки. В них фигурируют значения: n– объем выборочной совокупности и– выборочное среднее.

Рассмотрим аналогичные формулы для вычисления соответствующих параметров генеральной совокупности.

Формула для вычисления генеральной дисперсии будет иметь вид:

, (4.4)

где ²– генеральная дисперсия;

x_i– значение признака;

 – генеральная средняя;

N – объем генеральной совокупности.

Аналогом формулы (4.3) для генеральной совокупности является

. (4.5)

Свойства дисперсии

1) Прибавление константы Ск каждому значению не влияет на дисперсию:

.

2) Умножение каждого значения на Сувеличивает дисперсию вС²раз:

.

3. СТАНДАРТИЗИРОВАННЫЕ ДАННЫЕ

Часто желательно описать место некоторого значения в сово­купности, измеряя его отклонение от среднего всех значений в единицах стандартного отклонения.

Например, данная сово­купность 100 значений имеет среднее 18,75, а стандартное от­клонение 2,60. Если вам известно лишь, что среди этих 100 зна­чений есть одно, равное 20, то его относительное положение в множестве 100 значений видно не сразу.

Любое множество п данных со средним и стандартным отклонением S_x можно преобразовать в другое множество со средним 0 и стандартным отклонением 1 таким образом, что преобразованные значения будут непосредственно выражаться в отклонениях исходных значений от среднего, измеренных в еди­ницах стандартного отклонения. Новые значения называют зна­чениями z:

. (4.6)

Значение z не только удобное средство информации о по­ложении некоторого значения, связанного со средним и измерен­ного в единицах стандартного отклонения, но и шаг вперед к преобразованию множества X в произвольную шкалу с удоб­ными характеристиками среднего и стандартного отклонения. Сами оценки z могут не подходить для некоторых целей. Отри­цательные оценки, например, могут оказаться неудобными, а множество z будет, конечно, содержать дроби. Преобразование самих z позволяет устранить эти несущественные трудности.

Известно, что значения cz, полученные умножением каж­дого z на константу с, будут иметь стандартное отклонение с, а для cz+d среднее равно

.

Существует множество шкал измерения (произвольные сред­ние и стандартные отклонения), которые распространены в пе­дагогике и общественных науках. Множество данных можно расположить на любой шкале, то есть им можно приписать желаемые среднее (d) и стандартное отклонение (с), пользуясь выражением

y_i = cz_i + d. (4.7)

Например, оценки интеллектуального теста часто пре­образуются в шкалу со средним 100 и стандартным отклонением 15 или 16. Значения Т, полученные с помощью 10z+50, находят широкое применение.

Задача 4.2

Множество значений (0, 3, 4, 5, 6, 9, 10, 12,13, 15) необходимо перевести в шкалу со средним значением 100 и стандартным отклонением 15.

Решение

Найдем среднее значение по формуле (3.2) и стандартное отклонение по формуле (4.3):

;

.

По формуле (4.6) для каждого x_iнайдем значениеz_i . Вычисление оформим в виде таблицы 4.2.

Таблица 4.2

xi	zi	yi
0	-1,586	76,208
3	-0,968	85,478
4	-0,762	88,567
5	-0,556	91,657
6	-0,350	94,747
9	0,268	104,017
10	0,474	107,107
12	0,886	113,287
13	1,092	116,376
15	1,504	122,556

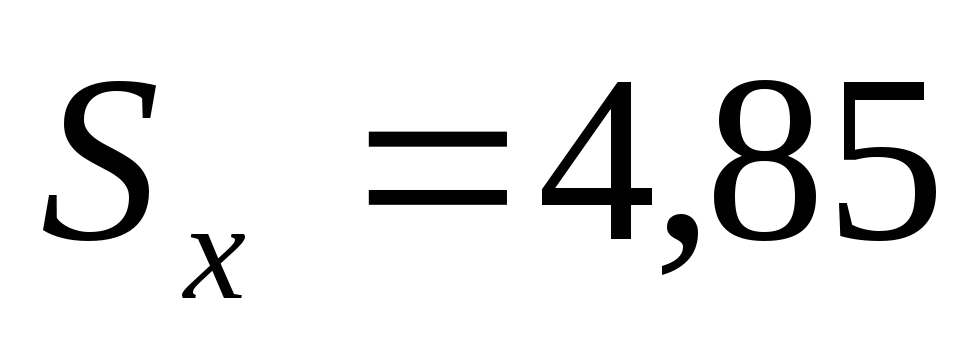
Подставляя каждое полученное значение z_i в формулу (4.7) и при условии, чтос=15 (новое стандартное отклонение) иd=100 (новое среднее значение), мы получим значенияу_iв новой шкале.

? ВОПРОСЫ И УПРАЖНЕНИЯ

1. Дайте определение размаху, выборочной дисперсии, генеральной дисперсии, стандартному отклонению. Воспроизведите формулы для их нахождения.

2. Что характеризует выборочная дисперсия.

3. Вычислите для множества: 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31 , 31, 31, 34, 36 размах, дисперсию, стандартное отклонение.

4. В каких случаях можно проводить сравнение разных выборок по дисперсиям?

5. Выборочные дисперсии результатов контрольной работы в классе 7«А» и 7«Б» соответственно равны 0,44 и 1,38. Какой вывод можно сделать при сравнении результатов контрольной работы в двух классах?

6. Дисперсия каждой из групп Aи В равна 5. Будет ли дисперсия 10 значений, полученных путем объединения групп, меньше, больше или равна 5?

Группа А: 13, 11, 10, 9, 7

Группа В: 28, 26, 25, 24, 22

7. Множество значений (-4, -2, 0, 1, 1, 3, 7, 12, 14, 15, 17) переведите в шкалу со средним значением 10 и стандартным отклонением 5.

ТЕМА 5