
- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
Білет 1
Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
Скінченні і нескінченні множини. Розглядаючи різні множини, ми помічаємо, що інколи можна, якщо не фактично, то хоча б принципово, назвати число елементів у певній множині. Такі, наприклад, множина всіх вершин деякого многогранника; множина всіх простих чисел, які не перевищують певного числа; множина всіх молекул води на Землі і т. д. Кожна з цих множин містить скінчене, хоча, можливо, і невідоме нам число елементів. З другого боку, існують множини, які складаються з нескінченного числа елементів. З другого боку, існують множини, які складаються з нескінченного числа елементів. Такі, наприклад, множина всіх натуральних чисел; множина всіх точок на прямій, всіх кругів на площині, всіх многочленів з раціональними коефіцієнтами тощо. При цьому, говорячи, що множина нескінченна, ми маємо на увазі, що з неї можна вилучити один елемент, два елементи і т. д., причому після кожного такого кроку в цій множині ще залишаться елементи.
Бієкцію — взаємно однозначна відповідність між елементами 2 множин, при якій кожному елементу однієї множини відповідає один і тільки один елемент іншої, і навпаки.
Зчисленні
(зліченні) множини. Найпростішою
серед нескінченних множин є множина
натуральних чисел. Назвемо зчисленною
множиною
всяку множину, елементи якої можна
бієктивно зіставити з усіма натуральними
числами. Інакше кажучи, зліченна множина
– це така множина, елементи якої можна
занумерувати в нескінченну послідовність:
 .
Наведемо приклади зліченних множин.
.
Наведемо приклади зліченних множин.
1. Множина всіх цілих чисел. Установимо відповідність між усіма цілими і всіма натуральними числами за такою схемою:
0 -1 1 -2 2 …,
1 2 3 4 5 …,
взагалі,
невід’ємному числу
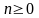 зіставимо непарне число
зіставимо непарне число
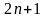 ,
а від’ємному
,
а від’ємному
 - парне число 2
- парне число 2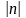 :
:
 при
,
при
,
 при
.
при
.
2.
Множина
всіх парних додатних чисел.
Відповідність очевидна:
 .
.
3.
Множина
 степенів числа 2. Тут
відповідність також очевидна. Кожному
числу
степенів числа 2. Тут
відповідність також очевидна. Кожному
числу
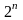 зіставляється число
зіставляється число
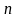 .
.
4.
Розглянемо складніший приклад, а саме,
покажемо, що множина
всіх раціональних чисел зліченна. Кожне
раціональне число однозначно записується
у вигляді нескоротного дробу
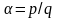 ,
,
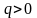 .
Назвемо суму
.
Назвемо суму
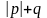 висотою
раціонального числа
висотою
раціонального числа
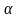 .
Зрозуміло, що число дробів з даною
висотою
скінченне. Наприклад, висоту
.
Зрозуміло, що число дробів з даною
висотою
скінченне. Наприклад, висоту
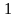 має тільки число
має тільки число
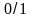 ;
висоту
;
висоту
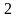 - числа
- числа
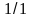 і -
,
висоту
і -
,
висоту
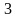 - числа
- числа
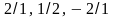 і
-
і
-
 і т. д. Нумеруватимемо всі раціональні
числа за зростанням висоти, тобто
спочатку випишемо числа висоти
,
потім – числа висоти
і т. д. При цьому всяке раціональне число
дістане деякий номер, тобто буде
встановлено взаємно однозначну
відповідність між всіма натуральними
і всіма раціональними числами.
і т. д. Нумеруватимемо всі раціональні
числа за зростанням висоти, тобто
спочатку випишемо числа висоти
,
потім – числа висоти
і т. д. При цьому всяке раціональне число
дістане деякий номер, тобто буде
встановлено взаємно однозначну
відповідність між всіма натуральними
і всіма раціональними числами.
Нескінченна множина, яка не є зліченною, називається незліченною множиною.
Установимо деякі спільні властивості зліченних множин.
Усяка підмножина зліченної множини скінченна або зліченна.
Доведення.
Нехай А
– зліченна множина, а В
– її підмножина. Занумеруємо елементи
множини А:
Нехай
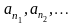 - ті з них, які входять у В.
Якщо серед чисел
- ті з них, які входять у В.
Якщо серед чисел
 є найбільше, то В скінченна, в противному
разі В зліченна, бо її члени
занумеровані числами
є найбільше, то В скінченна, в противному
разі В зліченна, бо її члени
занумеровані числами
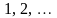
Сума будь-якої скінченої або зліченної множини зліченних множин є знову зліченна множина.
Доведення.
Нехай
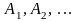 –
зліченні множини. Ми можемо вважати, що
вони попарно не перетинаються, бо інакше
ми розглянули б замість цих множин
–
зліченні множини. Ми можемо вважати, що
вони попарно не перетинаються, бо інакше
ми розглянули б замість цих множин
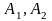 \
\ \
\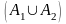 ,
… - кожна з яких не , - більш як зліченна,
- що мають ту саму суму, що й множини
Усі елементи множин
можна записати у вигляді такої нескінченної
таблиці:
,
… - кожна з яких не , - більш як зліченна,
- що мають ту саму суму, що й множини
Усі елементи множин
можна записати у вигляді такої нескінченної
таблиці:
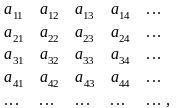
де
в першому рядку стоять елементи множини
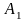 ,
у другому – елементи множини
,
у другому – елементи множини
 і т. д. Занумеруємо тепер всі ці елементи
«по діагоналях», тобто за перший елемент
візьмемо
і т. д. Занумеруємо тепер всі ці елементи
«по діагоналях», тобто за перший елемент
візьмемо
 ,
за другий
,
за другий
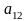 ,
за третій
,
за третій
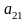 і т. д., рухаючись так, як показано
стрілками на такій таблиці:
і т. д., рухаючись так, як показано
стрілками на такій таблиці:

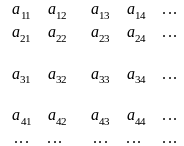
Зрозуміло, що при цьому кожний елемент кожної з множин дістане певний номер, тобто буде встановлено взаємно однозначну відповідність між усіма елементами всіх множин і всіма натуральними числами. Наше твердження доведено.
Будь-яка нескінченна множина містить зліченну підмножину.
Доведення.
Нехай М
– нескінченна множина. Виберемо в ній
довільний елемент
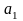 .
Оскільки М
нескінченна, у ній знайдеться елемент
.
Оскільки М
нескінченна, у ній знайдеться елемент
 ,
відмінний від
і від
,
і т. д. Продовжуючи цей процес (який не
може обірватись через «нестачу»
елементів, бо М
нескінченна), ми дістанемо зліченну
підмножину
,
відмінний від
і від
,
і т. д. Продовжуючи цей процес (який не
може обірватись через «нестачу»
елементів, бо М
нескінченна), ми дістанемо зліченну
підмножину
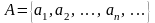 множини М.
множини М.
Еквівалентність множин. Порівнюючи ті чи інші нескінченні
множини з натуральним рядом, ми прийшли до поняття зліченної множини. Зрозуміло, що множини можна порівнювати не тільки з множинами натуральних чисел; встановлення взаємно однозначної відповідності (бієкції) дає змогу порівнювати між собою будь-які дві множини. Введемо таке означення:
Означення. Дві множини, М і N, називаються еквівалентними (позначення M ~ N), якщо між їхніми елементами можна встановити взаємно однозначну відповідність.
Поняття еквівалентності застосовне до будь-яких множин, як скінченних, так і нескінченних. Дві скінченні множини еквівалентні між собою тоді (і тільки тоді), коли число елементів у них однакове. Означення зліченної множини можна тепер сформулювати так: множина називається зліченною, якщо вона еквівалентна множині натуральних чисел.
Зрозуміло, що дві множини, еквівалентні третій, еквівалентні між собою; зокрема, всі зліченні множини еквівалентні між собою.
Незліченність множини дійсних чисел.
Теорема 1. Множина дійсних чисел, замкнутих між нулем і одиницею, незліченна.
Доведення. Припустимо, що дано якусь зліченну множину (всіх чи тільки деяких) дійсних чисел , що лежать на відрізку [0,1].
 (1)
(1)
Тут
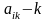 -а
десяткова цифра
-а
десяткова цифра
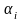 .
Побудуємо дріб
.
Побудуємо дріб

діагональною
процедурою Кантора,
а саме: за
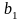 візьмемо довільну цифру, яка не збігається
з
,
за
візьмемо довільну цифру, яка не збігається
з
,
за
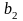 - довільну цифру, яка не збігається з
- довільну цифру, яка не збігається з
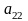 ,
і т. д., взагалі, за
,
і т. д., взагалі, за
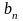 візьмемо довільну цифру, яка не збігається
з
візьмемо довільну цифру, яка не збігається
з
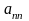 .
Цей десятковий дріб не може збігтися
ні з одним дробом, що міститься в переліку
(1). Справді, від
.
Цей десятковий дріб не може збігтися
ні з одним дробом, що міститься в переліку
(1). Справді, від
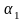 дріб
дріб
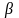 відрізняється принаймні першою цифрою,
від
відрізняється принаймні першою цифрою,
від
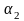 - першою цифрою і т. д., взагалі, оскільки
- першою цифрою і т. д., взагалі, оскільки
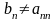 для всіх
,
то дріб
відмінний від будь-якого з дробів
для всіх
,
то дріб
відмінний від будь-якого з дробів
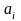 ,
що входять у перелік (1). Отже, ніяка
зліченна множина дійсних чисел, які
лежать на відрізку [0, 1], не вичерпує
цього відрізка.
,
що входять у перелік (1). Отже, ніяка
зліченна множина дійсних чисел, які
лежать на відрізку [0, 1], не вичерпує
цього відрізка.
Наведене
доведення містить невеликий «обман».
Справа в тому, що деякі числа (а саме,
числа виду
 )
можна записати у вигляді десяткового
дробу двома способами з нескінченною
кількістю нулів або з нескінченною
кількістю дев’яток; наприклад,
)
можна записати у вигляді десяткового
дробу двома способами з нескінченною
кількістю нулів або з нескінченною
кількістю дев’яток; наприклад,

Таким чином, незбіг двох десяткових дробів ще не гарантує відмінності чисел, які вони зображують.
Однак,
якщо дріб
будувати обережніше, так, щоб він не
містив ні нулів, ні дев’яток, припускаючи,
наприклад, що
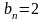 , коли
, коли
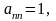 і
і
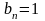 ,
коли
,
коли
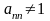 ,
то доведення стає цілком коректним.
,
то доведення стає цілком коректним.
Отже, відрізок [0, 1] дає приклад незліченної множини.
Наведемо деякі приклади множин, еквівалентних відрізку [0, 1]:
Множина всіх точок будь-якого відрізка [a, b] або інтервала (a,b).
Множина всіх точок на прямій.
Множина всіх точок площини, простору, поверхні сфери, точок, які
лежать всередині сфери, і т. д.
Множина всіх прямих на площині.
Множина всіх неперервних функцій однієї чи кількох змінних.
Поняття потужності множини. Якщо еквівалентні дві скінченні множини, то вони складаються з тієї самої кількості елементів. Якщо ж еквівалентні між собою множини М і N довільні, то кажуть, що М і N мають однакову потужність. Отже, потужність — це те спільне, що є в усіх еквівалентних між собою множин. Для скінченних множин поняття потужності збігається із звичним поняттям кількості елементів множини. Потужність множини натуральних чисел. Про множини, еквівалентні множині всіх дійсних чисел відрізка [0;1], кажуть, що вони мають потужність континууму. Цю потужність позначають символом с.
