2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.

Орієнтований граф — впорядкована пара множин (I,U), де I — непорожня множина вершин графа, що позначаються натуральними числами (I  N), U — множина впорядкованих пар (i,j), що називаються дугами, та (i,j)  I x I.

Вершина i дуги (i,j) називається її початком, а j — її кінцем.

Геометрично орієнтований граф зображується точками (множина вершин I) та лініями зі стрiлками (множина дуг U), що з'єднують деякі пари цих точок. На рис. 1 зображено граф g=(I,U), для якого I={1,2,3,4,5}, U={(1,3),(1,2),(2,1),(5,2),(4,5),(4,3)}

рис. 1.1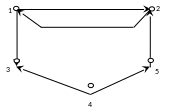

Шляхом орієнтованого графа g називається послідовність його дуг {u₁, u₂, … u_m}, для якої початок кожної наступної дуги, починаючи з другої, співпадає з кінцем попередньої дуги. Наприклад, на рис.1.1 шляхом є послідовність дуг {(4,5),(5,2)}.

Контуром орієнтованого графа g називається шлях графа {u₁, u₂, … u_m}, для якого кінець останньої дуги співпадає із початком першої дуги. Наприклад, на рис.1.1 шляхом є послідовність дуг {(1,2),(2,1)}.

Неорієнтований граф — впорядкована пара множин (I,U), де I — непорожня множина вершин графа, що позначаються натуральними числами (I  N), U — множина невпорядкованих пар (i,j), що називаються ребрами, та (i,j)  I x I.

Геометрично неорієнтований граф зображується точками (множина вершин I) та лініями (множина дуг U), що з'єднують деякі пари цих точок. На рис. 1.2 зображено граф g=(I,U), для якого I={1,2,3,4,5}, U={(1,3),(1,2),(2,5),(4,5),(3,4)}

2

рис. 1.2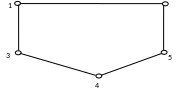

Ланцюг неорієнтованого графа — послідовність його ребер {u₁, u₂, … u_m}, для якої одна вершина кожного наступного ребра, починаючи з другого, є вершиною попереднього, а інша вершина є вершиною наступного ребра. Наприклад, на рис.1.2 ланцюгом є послідовність ребер {(1,3),(4,3)}.

Цикл неорієнтованого графа — називається ланцюг {u₁, u₂, … u_m}, для якого u₁=u_m. Наприклад, на рис.1.2 циклом є ланцюг {(1,3),(3,4),(5,4),(2,5),(2,1)}.

Розглядатимемо орієнтовані графи.

Мережею називається граф, елементам якого поставлені у відповідність деякі параметри. Елементами графа вважаються його вершини, дуги.

Побудуємо мережу таким чином:

1. кожній вершині iI поставимо у відповідність число d_i, що називається її інтенсивністю. Вершина i називається джерелом, якщо d_i>0, і стоком, якщо d_i<0, i нейтральною, якщо d_i=0;

2. кожній дузі (i,j)U поставимо у відповідність числа r_ij та c_ij, що називаються, відповідно, пропускною спроможністю та собівартістю.

Потоком в одержаній мережі називається сукупність величин x_ij, (i,j)U, що задовольняють умовам:

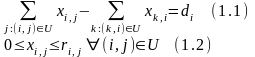
Нехай V⊂I.

Пропускною спроможністю розрізу U(V) називається величина

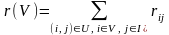
Теорема 1.1 Для того, щоб на мережі існував потік x = {xij, (i,j)∈U}, необхідно i достатньо, щоб d(I)=0 i для довільної множини V⊂I виконувалась умова d(V)≤r(V), де

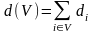(1.3)

Кожному потоку x = {xij, (i,j)∈U} поставимо у відповідність цільову функцію

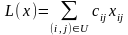(1.4)

Лiнiйна задача на мережі (або задача про оптимальний потік на мережі) полягає у пошуку допустимого потоку x на мережі, що мiнiмiзує цільову функцію L(x), тобто

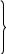
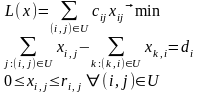(1.5)

Допустимий потік x називається оптимальним, якщо він доставляє мінімальне значення функції L(x).

Задача про найкоротший шлях. Метод Мінті

Нехай маємо де–яку мережу g=(I,U), 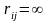, — довжина дуги (собівартість перевезення одиниці продукту по дузі).

Розглянемо також дві фіксовані вершини i₁, i_s графа g та довільний шлях, що з'єднує i₁ та i_s:

l(i₁,is)=((i₁,i₂),(i₂,i₃),...,(i_s-1,i_s))=(u₁,u₂,u₃,...,u_s-1), де i_t  I, t={1,..,s}.

Тоді собівартість перевезення даним шляхом визначається як

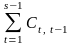
Задача про найкоротший шлях (про вибір найбільш економного шляху) полягає в пошуку шляху (u₁,u₂,u₃,...,u_s-1), що мiнiмiзує . Шуканий шлях називається найкоротшим (оптимальним).

Метод Мiнтi

Крок 1. Позначається вершина i₁ (коренева вершина) позначкою =0, I(1) = {i₁} — множина позначених вершин.

Крок (r+1). Розглянемо множину J(r)={...,i_µ,...} непозначених вершин i_µ: (i_λ,i_µ)U, i_λI(r), i_µJ(r), I(r)∩J(r)=. Для кожної з таких дуг (i_λ,i_µ) знаходимо суму

h_iλ+c_iλiµ,

виділяємо ті дуги, для яких ця сума мінімальна. При цьому з декількох дуг, що підлягають виділенню i закінчуються в одній i тій же вершині, виділяється лише одна.

Позначаємо кінці виділених дуг числом, що дорівнює мінімальному значенню h_iλ+c_iλiµ. За рахунок позначених вершин множина I(r) розширюється до множини I(r+1).

Вказаний процес продовжується до тих пір, поки серед позначених не з'явиться вершина i_s, або подальше позначення неможливе.

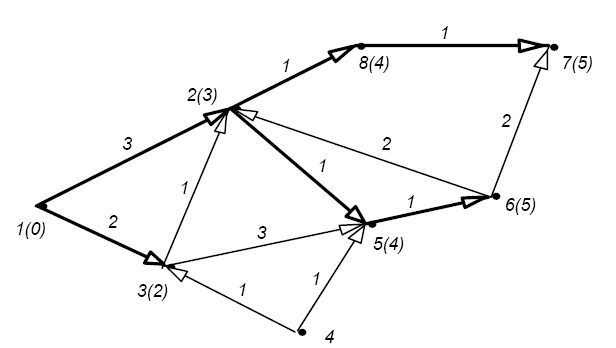
Рис. 2.3

Крок 3. Розглядаються дуги

(1,2) : h₁ + c₁₂ = 3,

(3,2) : h₃ + c₃₂ = 3,

(3,5) : h₃ + c₃₅ = 5.

Мiнiмальна з підрахованих величин відповідає дугам (1,2), (3,2). Видiлимо дугу (1,2), h₂ = 3, I(3) = {1,2,3}.

Крок 4. Розглядаються дуги

(2,5) : h₂ + c₂₅ = 4,

(2,8) : h₂ + c₂₈ = 4,

(3,5) : h₃ + c₃₅ = 5.

Видiляємо дуги (2,5), (2,8), h₅=4, h₈=4, I(4)={1,2,3,5,8}.

Крок 5. Розглядаються дуги

(5,6) : h₅ + c₅₆ = 5,

(8,7) : h₈ + c₈₇ = 5.

Видiляємо дуги (5,6), (8,7), h₆ = 5, h₇ = 5, I(5) = {1,2,3,5,6,7,8}.

Найкоротший шлях з вершини 1 у вершину 6 — це шлях l*(1,6) = (1,2,5,6). Знаходиться він переглядом виділених дуг від вершини 6 до вершини 1. При цьому C(l*(1,6)) = h₆ = 5.