1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.

Під множиною розуміють сукупність об’єктів довільної природи, які мають спільну властивість.

Об’єкти, з яких складається множина, називають її елементами. Якщо а є елементом множини А, то це символічно записують так: аА. Вираз аА (або 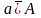) означає, що а не є елементом множини А.

Множина вважається заданою, якщо про кожний об’єкт можна сказати, є він елементом цієї множини, чи ні. Задати множину можна двома способами: переліком елементів та за допомогою характеристичної властивості, яку мають всі елементи даної множини.

Множина, яка складається з обмеженого числа елементів, називається скінченною. Множина, яка не містить жодного елемента, називається порожньою і позначається символом .

Означення 1. Якщо кожен елемент множини А є елементом множини В, то говорять, що множина А включається в множину В, або множина В включає множину А, або А є підмножиною множини В і позначають АВ. Іно­ді використовують позначення АВ, наголошуючи тим самим на мож­ливість співпадання (рівності) множин.

Означення 2. Множини А і В називаються рівними (записують А = В), якщо вони складаються з одних і тих же елементів, тобто множина А є підмножиною множини В, а В – підмножиною множини А.

Виходячи з означення підмножини, можна дати і таке означення рівності двох множин:

Означення 3. Множини А і В називаються рівними, якщо кожен елемент множини А є елементом множини В і навпаки, кожен елемент множини В є елементом множини А.

Звідси отримуємо правило встановлення рівності двох множин:

Для того щоб довести рівність двох множин А і В, потрібно взяти будь-який елемент з множини А і показати, що він належить множині В. Після цього взяти будь-який елемент з множини В і показати, що він належить множині А.

Встановлено, що для будь-якої n-елементної множини існує 2ⁿ різних підмножин. Множину всіх підмножин множини А називають булеаном множини А і позначають (А).

Існують множини, по відношенню до яких всі інші множини є підмножинами. Такі загальні множини називають універсальними і позначають буквою U.

Для множин можна ввести ряд операцій, результатом виконання яких також будуть множини.

Означення 4. Об’єднанням множин А і В (позначається AB) називається множина, яка складається з тих і тільки тих елементів, які належать хоча б одній з множин А чи В. Тобто AB={х| хА  хВ}.

Означення 5. Перетином множин А і В (позначається AB) називається множина, яка складається з тих і тільки тих елементів, які належать множинам А і В одночасно. Тобто AB={х| хА  хВ}.

Означення 6. Різницею множин А і В (позначається A\B) називається множина, яка складається з тих і тільки тих елементів, які належать множині А і не належать множині В. Тобто A\B={х| хА  хВ}.

Означення 7. Симетричною різницею множин А і В (позначається A∆B) називається множина, яка складається з тих і тільки тих елементів, які належать множині А і не належать множині В, або належать множині В і не належать множині А. Тобто A∆B={х| (хА  хВ)( хВ  хА)}.

Означення 8. Доповненням множини А до універсальної множини U (позначається 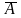) називається множина всіх елементів універсальної множини, які не належать множині А. Тобто ={х| х U  хА}.

Неважко помітити, що = U \ А.

Для кращого розуміння операцій над множинами іноді користуються спеціальними геометричними схемами, які називаються діаграмами Ейлера-Венна.

Для визначення порядку дій над множинами в теоретико-множинних виразах вводять дужки. Якщо у виразі дужки відсутні, то операції виконуються в такій послідовності: доповнення, перетин, об’єднання, різниця, симетрична різниця.

Під впорядкованою парою (a, b) розуміють двохелементну множину {a, b}, про яку можна сказати, який елемент стоїть на першому місці, а який – на другому. При цьому елемент a називається першою компонентою впорядкованої пари, а еле­мент b – другою. Якщо (a, b) і (c, d) впорядковані пари, то (a, b) = (c, d) то­ді і тільки тоді, коли а = с і b = d.

Аналогічно вводиться впорядкована трійка, четвірка і, взагалі, впорядкована n-ка, тобто впорядкована сукупність n елементів.

Означення 1. Прямим (декартовим) добутком множин А і В (позна­чається АВ) називають множину всеможливих впорядкованих пар (a, b), де аА, а bВ.

Тобто АВ = {( a, b) | аА  bВ}.

Можна розглядати прямий добуток довільної скінченої сукупності множин. Якщо А = В, то АА називають декартовим квадратом множини А і позначають А². Взагалі кажучи, декартовий добуток множини А на себе n разів, тобто множину АА...А, називають n-им декартовим (або прямим) степенем множини А і позначають Аⁿ.

Означення 2. n-арним (n-місним) відношенням називається всяка під­множина прямого добутку n множин.

Найбільш часто зустрічаються та найбільш вивченими є бінарні (тобто двомісні) відношення. Тому надалі зоглядатимемо лише бінарні відношення.

Якщо елемент а перебуває у відношенні  з елементом b, то це позначають так: (a, b), або a b.

b

Задавати відношення, як і множини, можна за допомогою характе­ристич­ної властивості, або за допомогою переліку всіх його елементів. Крім того, існують спеціальні способи задання відношень: графом, таблицею, матрицею, графіком.

Множина перших компонент називається областю визначення відношення, множина других – множиною значень.

Над відношеннями можна виконувати всі відомі теоретико-множинні операції: перетин, об’єднання і т.д. Крім того, для відношень можна означити ще дві операції – композицію та інверсію відношень.

Означення 3. Композицією відношень  і  називається відношення  ◦ , елементами якого є пари (a, b), для кожної з яких існує такий еле­мент с, що (a,с) і (с,b) .

Означення 4. Відношення ­ ^–1 називається оберненим (інверсним) до відноше­ння , якщо (b, a)­ ^-1 тоді і тільки тоді, коли (a, b).

Розглянемо властивості, за якими класифікують відношення.

Означення 5. Відношення  називається рефлексивним на множині А, якщо для будь-якого елементу аА пара (a, a).

Означення 6. Відношення  називається антирефлексивним на множині А, якщо ні для якого елементу аА не виконується (a, a).

Означення 7. Відношення  називається симетричним на множині А, якщо для всіх елементів a, bА таких, що (a, b), виконується (b, a).

Означення 8. Відношення  називається антисиметричним на множині А, якщо для всіх елементів a, bА таких, що (a, b) і (b, a) вико­нується a = b.

Означення 9. Відношення  називається транзитивним на множині А, якщо для будь-яких елементів a, b, сА з того, що (a, b) і (b, с) ви­пли­ває, що (а, с).

Означення 10. Відношення  називається зв’язним (досконалим) на множині А, якщо для будь- яких двох елементів a, bА таких, що a  b має місце хоча б одне із співвідношень: (a, b) або (b, a).

Означення 11. Відношення , задане на множині А, називається відно­шенням еквівалентності, якщо воно рефлексивне, симетричне і транзи­тивне.

З відношенням еквівалентності тісно пов’язане поняття розбиття мно­жини на класи.

Означення 12. Сукупність підмножин множини А називається розбиттям множини на класи, якщо ці підмножини непорожні, взаємно неперерізні і їх об’єднання співпадає з множиною А.

Означення 13. Класом еквівалентності, породженим елементом а, називається множина тих елементів з множини А, які перебувають у від­ношення еквівалентності  з елементом а.

Символічно можна записати так: К_а = {х | хА і (х, а)}.

Теорема. Всяке відношення еквівалентності, задане на множині А, задає розбиття множини на класи і, навпаки, всяке розбиття множини на класи задає на цій множині відношення еквівалентності.

Доведення. І етап. Нехай на множині А задано відношення еквівалентності . Очевидно, що множина А не порожня. Тоді існує елемент, наприклад, аА. Побудуємо клас еквівалентності К_а. Може бути два випадки: К_а=А або К_аА. В першому випадку теорема доведена, адже множина розбивається на один клас. В другому випадку, оскільки К_аА і К_аА, існує елемент b: bА і bК_а.

Побудуємо клас еквівалентності К_b. К_bА і К_b . Покажемо, що К_аК_b=. Припустимо супротивне. Тоді існує елемент c такий, що хК_b i хК_а. В силу означення класу еквівалентності одержимо (х,b) і (х,а) або (оскільки відношення еквівалентності симетричне) (b,х) і (х,а). В силу транзитивності відношення еквівалентності звідси отримуємо, що (b,а), тобто bК_а, що суперечить вибору елемента b. Одержана суперечність доводить, що К_аК_b=.

Знову може бути два випадки: К_аК_b=А або К_аК_b А. В першому випадку теорема доведена. В другому випадку існує елемент с: сА, сК_а, сК_b. Побудуємо клас еквівалентності К_с і т.д. В кінці кінців побудуємо скінчену або нескінчену множину класів еквівалентності, які задають розбиття множини на класи.

Прикладом розбиття на скінчену множину класів є розбиття учнів на класи чи студентів на групи, а на нескінчену – розбиття множини прямих на площині за відношенням паралельності.

ІІ етап. Нехай задано розбиття множини А на класи. Задамо на множині відношення  в такий спосіб: будемо вважати що два елементи перебувають у відношенні , якщо вони належать до одного і того ж класу. Очевидно, що таке відношення рефлексивне і симетричне. Якщо елемент b належить до того класу, що а і с елемент до того класу, що b , то елемент с належить до того класу, що а. Тому відношення транзитивне, отже і є відношенням еквівалентності. Теорема доведена.

Означення 14. Сукупність усіх класів еквівалентності за відношенням  називається фактор-множиною множини А за відношенням  і позна­чається А/.

Означення 15. Відношення , задане на множині А, називається від­ношенням порядку, якщо воно антисиметричне і транзитивне.

Якщо відношення порядку  – рефлексивне, то його називають нестро­гим порядком. Якщо ж відношення порядку  – антирефлексивне, то це бу­­де відношення строгого порядку. Відношення порядку називається лінійним, якщо воно зв’язне. Якщо ж відношення порядку незв’язне, то його називають відношенням часткового порядку.

Множина, на якій задано відношення порядку, називається впорядко­ва­ною. Залежно від типу відношення порядку вона може бути строго або нестро­го впорядкованою, частково або лінійно впорядкованою.

Білет24