
- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
На практиці зустрічаються задачі, в яких необхідно підрахувати число всеможливих способів розміщення деяких предметів скінченої множини або число всіх можливих способів виконання певної дії, маючи в арсеналі скінчену множину таких дій. Оскільки при розв’язанні задачі доводиться комбінувати з наборами предметів чи методів, то задачі такого типу називають комбінаторними, а методи їх розв'язку – методами комбінаторного аналізу.
Більшість комбінаторних задач можна розв’язати, використовуючи наступні правила:
Правило суми. Якщо об’єкт А можна вибрати m способами, а інший об’єкт В – іншими n способами, то вибір або А, або В можна здійснити m+n способами.
Правило добутку. Якщо об’єкт А можна вибрати m способами і після кожної такої вибірки об’єкт В можна вибрати n способами, то вибір пари об’єктів А і В в заданому порядку можна здійснити mn способами.
Правила суми та добутку, в якійсь мірі, є в якійсь мірі універсальними при розв’язанні комбінаторних задач. Разом з тим ряд задач зводиться до часткових випадків, де використовують формули обчислення, які відразу дають розв’язок задачі. Такими частковими випадками є розміщення, перестановки та комбінації.
Означення 1. Розміщенням з n по k елементів з повторенням називається будь-яка впорядкована k‑елементна підмножина n-елементної множини, елементи якої можуть повторюватись.
Число
всіх розміщень з повторенням з n по k
елементів позначають
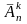 і обчислюють за формулою
=
nk.
Наприклад, кількість різних трицифрових
чисел, які складаються лише з непарних
цифр, обчислюється за формулою
і обчислюють за формулою
=
nk.
Наприклад, кількість різних трицифрових
чисел, які складаються лише з непарних
цифр, обчислюється за формулою
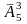 =53=125.
=53=125.
Означення 2. Розміщенням з n по k елементів без повторень називається будь-яка впорядкована k‑елементна підмножина n-елементної множини.
Число всіх розміщень з n по k елементів позначають і обчислюють за формулою = n(n—1)(n—2)...(n—k+1). Наприклад, число різних варіантів прогнозування переможців турніру серед десяти учасників (1-ше, 2-ге та 3-тє місця) обчислюється за формулою: 10 9 8 =720.
Означення 3. Упорядковані множини, які відрізняються одна від одної лише порядком своїх елементів (тобто можуть бути одержані з однієї і тієї ж множини перестановкою своїх елементів), називаються перестановками. Очевидно, що перестановка – це розміщення з n по n елементів.
Число всіх перестановок n-елементної множини позначають Рn і обчислюють за формулою Рn = n!.
Цю формулу отримуємо з формули розміщень:
Рn
= =
n(n–1)(n–2)...(n–n+1)
=
12...n
= n!.
=
n(n–1)(n–2)...(n–n+1)
=
12...n
= n!.
Згідно цієї формули п’ятеро гостей за столом можна розмістити 5! = 120 способами.
Існують задачі на перестановки, в яких всі елементи множини розрізняються між собою та задачі, в яких можна виділити набори (кортежі), в яких деякі елементи співпадають. Наприклад, повторюються окремі літери в слові “мама”, цифри в числі 122 і т.д. Такі задачі називають задачами на перестановки з повтореннями.
При
обчисленні перестановок з повторенням
елементи, що співпадають, групують по
типах. Тоді число різних перестановок,
які можна утворити з n
елементів, серед яких є k1
елементів першого типу, k2
елементів
другого типу, ..., km
елементів
m-го
типу, дорівнює Рn(k1,k2,...,km)=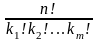 .
Якщо елемент не повторюється, то
відповідний кортеж складається лише з
одного елементу.
.
Якщо елемент не повторюється, то
відповідний кортеж складається лише з
одного елементу.
Отже,
переставляючи літери в слові “мама”,
можна утворити
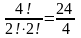 =
6 різних слів, чисел, переставляючи цифри
в числі 122, можна одержати
=
6 різних слів, чисел, переставляючи цифри
в числі 122, можна одержати
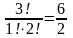 =
3.
=
3.
Означення 4. Комбінацією без повторень з n по k елементів називається будь-яка k-елементна підмножина n-елементної множини.
Комбінації
відрізняються від розміщення лише тим,
що відсутня умова впорядкованості
підмножини. Число всіх комбінацій з n
по
k елементів
позначають
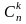 і обчислюють за формулою:
і обчислюють за формулою:
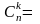
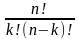 .
.
Мають
місце рівності
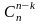 та
та
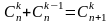 ,
які часто використовують на практиці.
,
які часто використовують на практиці.
Означення 5. Комбінацією з повтореннями з n по k елементів називається будь-яка k-елементна підмножина n-елементної множини, елементи якої можуть повторюватись.
Число
всіх комбінацій з повторенням з n
по
k
елементів
позначають
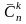 і має місце формула
і має місце формула
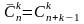 .
.
Так,
утворити букет з 5-ти квіток трьох сортів
можна
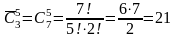 .
.
Біноміальна
теорема. Для
будь-якого натурального числа n
має місце формула
(a+b)n=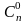 anb0+
anb0+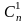 an–1b1+
an–1b1+ an–2b2+…+
an–2b2+…+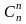 a0bn.
a0bn.
Доведення. Доведення проведемо методом математичної індукції.
1)
При n=1
маємо:
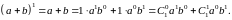
2)
Припустимо, що формула справедлива для
деякого натурального числа k,
тобто,
що має місце рівність
(a+b)k=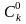 akb0+
akb0+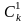 ak–1b1+
ak–1b1+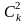 ak–2b2+…+
ak–2b2+…+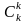 a0bk.
a0bk.
3) Доведемо справедливість формули для числа k +1.
(a+b)k+1=(a+b)k(a+b)=( akb0+ ak–1b1+ ak–2b2+…+ a0bk )(a+b)=
= ak+1b0+ akb1+ ak–1b2+…+ a1bk +
+ akb1+ ak–1b2+ ak–2b3+…+ a0bk+1 =
= ak+1b0+( + )akb1+( + )ak–1b2+…+ a0bk+1=
=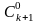 ak+1b0+
ak+1b0+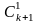 akb1+
akb1+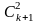 ak–1b2+…+
ak–1b2+…+ a1bk
.
a1bk
.
Тоді в силу методу математичної індукції теорема має місце для всіх натуральних чисел n.
Теорема доведена.
Наступна теорема є узагальненням біному Ньютона і дає відповідь на те, як розкривати дужки при обчисленні виразу виду (a1 + a2 + ... + ak)n.
Поліноміальна
теорема. Вираз (a1 +
a2
+
... + ak)n
дорівнює сумі всіх можливих доданків
виду
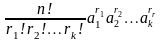 ,
де
,
де
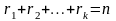 ,
тобто
,
тобто
(a1
+
a2
+
... + ak)n
=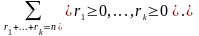
Доведення.
Перемножимо послідовно суму a1
+
a2
+
... + ak
на себе n
раз.
Тоді одержимо kn
доданків виду d1d2…dn,
де кожен множник di
дорівнює або
a1,
або a2
,…,
або ak.
Позначимо через B(r1,
r2,…,
rk)
сукупність всіх тих доданків, де a1
зустрічається
множником r1
раз, a2
–
r2
раз,…, ak
– rk
раз. Число таких доданків дорівнює
Pn(r1,
r2,…,
rk).
Відомо, що Pn(r1,
r2,…,
rk)
=
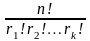 .
.
Отже, (a1 + a2 + ... + ak)n = Теорема доведена.
Білет 28
