1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.

Лінійна кореляція

Досить часто функції регресії виявляються лінійними, тобто

f(x)=ax+b(7) g(y)=cy+d(8)

Означення 5. Якщо обидві функції регресії f(x) і g(y) лінійні, то кореляцію називають лінійною

Очевидно, що для лінійної кореляції обидві лінії регресії є прямими лініями. Рівняння прямих набувають вигляду

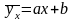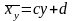(9); (10)

Задача полягає в тому, Щоб за результатами вибірки оцінити значення невідомих коефіцієнтів а, b, с, d.

а) метод найменших квадратів

Припустимо, що проведено п незалежних дослідів, внаслідок чого отримано п пар чисел

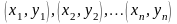(11)

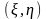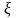Ці пари чисел можна розглядати як випадкову вибірку p генеральної сукупності всіх можливих значень випадкового вектора . Величини і рівняння, знайдеш за результатами вибірки (11). називають вибірковими Розглянемо спочатку найпростіший випадок, коли різні значення , і відповідні їм значення 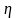спостерігались по одному разу. Тоді немає необхідності використовувати поняття умовного середнього значення і рівняння регресій (5), (6) можна переписати так.

y=ax+b,(12); х = су +d.(13)

На початку XIX ст Лежандр і Гаусс незалежно один від одного запропонували метод, який широко використовується для побудови емпіричних формул. Суть методу полягає в тому, що невідомі коефіцієнти емпіричної формули вибираються так, щоб сума квадратів відхилень значень, які спостерігались, від їх істинного .значення була мінімальною. Цей метод називають методом найменших квадратів або методом Гаусса.

Примітка. Результати вибірки можна зобразити точками на площині відносно прямокутної системи координат (по осі абсцис відкладено значення , а по осі ординат - значення ) Сукупність точок 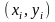називають полем кореляції. З'єднавши точки відрізками отримаємо ламану лінію, яку називають емпіричною лінією регресії По вигляду ламаної можна зробити висновок про форму кореляційного зв'язку.

Означення . Якщо хоч одна з функцій регресії нелінійна, то кореляцію називають нелінійною (криволінійною).

В цьому випадку лінія регресії – не деяка крива, відмінна від прямої. На практиці часто зустрічається випадки параболічної кореляції деякого порядку

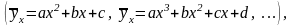гіперболічної кореляції 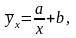показникової кореляції і т. д, Теорія нелінійної кореляції розв'язує ті ж задачі, що й теорія лінійної кореляції, тобто задачі встановлення форми і сили кореляційного зв'язку.

Побудувавши поле кореляції можна висунути певну гіпотезу про форму зв'язку.

Для відшукання невідомих параметрів рівняння регресії використовують метод найменших квадратів.

2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.

Задачею опуклого програмування є задача (1)-(2), для якої f(x) – функції опуклі:

(1)

при обмеженнях

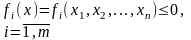(2)

або задачі (1)-(3), де обмеження 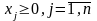(3):

, (3)

де f_i та f є опуклими функціями.

Функція Лагранжа. Теореми Куна-Таккера.

Нехай маємо задачу опуклого програмування (1)-(3). Тоді функцією Лагранжа будемо називати:

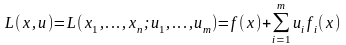
Умова Слейтера.

Кажуть, що система обмежень (2) задовольняє умову Слейтера, якщо:

.

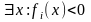Теорема Куна-Таккера 1.

Для того, щоб точка , яка є допустимим розв’язком задачі опуклого програмування (1)-(3) була оптимальним розв’язком цієї задачі, необхідно і досить, щоб існувала така точка 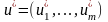, що є сідловою точкою функції Лагранжа 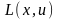на множині 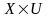, де

X – множина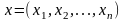 , що

U – множина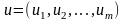 , що

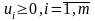
тобто:

,

.

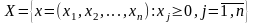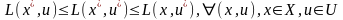Теорема Куна-Таккера 2.

Припустимо, що f(x) та f_i(x) з (1)-(3) мають неперервні часткові похідні по всіх змінних x_j

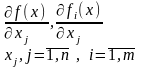
є неперервно-диференційовні функції.

Тоді для того, щоб точка 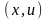була сідловою точкою функції Лагранжа на множині , необхідно і досить, щоб вона задовольняла таким співвідношенням:

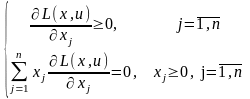(4)

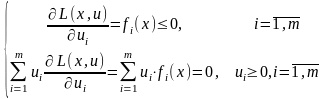(5)

Із співвідношень (4)-(5) робимо висновок, що теорему Куна-Таккера 2 можна записати в такій еквівалентній формі:

для того, щоб була сідловою точкою функції Лагранжа на множині необхідно і досить, щоб для неї виконувалися такі співвідношення:

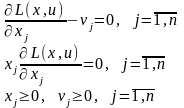(6)

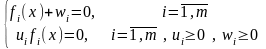(7)

Припустимо, що система обмежень (2) задовольняє умові Слейтера. То на основі останнього і теореми Куна-Таккера 1 приходимо до такої теореми:

для того, щоб вектор х був оптимальним розв’язком задачі опуклого програмування (1)-(3) при умові виконання умов теореми Куна-Таккера 2, необхідно і досить, щоб існували такі вектори:

які задовольняють таким співвідношенням:

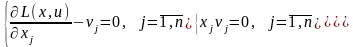(8)

(9)

Задача опуклого квадратичного програмування

Квадратичний сиплекс метод.

Нехай 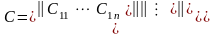є визначеною і симетричною

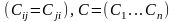фіксований вектор, тоді задача

визначити 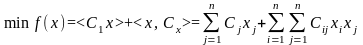(10)

при обмеженнях 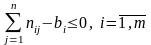(11)

(12)

називається задачею квадратного програмування.

Для цієї задачі функція Лагранжа має вигляд:

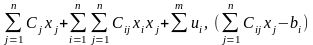
На основі попереднього параграфа при виконанні умов Слейтера.

Для цієї задачі типу 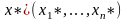буде оптимальним розв’язком (10)-(12) тоді і тільки тоді коли 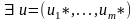, що

.

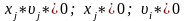
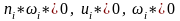Отже, для того щоб вектор x був оптимальним розв’язком задачі (10)-(12) необхідно і досить, щоб існували такі вектори , 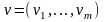, , 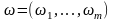такі, що:

(13)

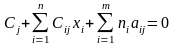
(14)

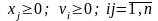
(15)

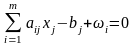
(16)

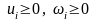
(17) .

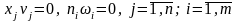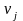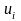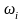Рекомендації, щодо розв’язування задачі (10)-(12). Використовуючи сиян таблиці знаходять базисний допустимий розв’язок даної задачі лінійного програмування обмеження якої будуть обмеження (13)-(16). Але, такий що серед змінних та одна базисна, а інша небазисна, а І також серед змінних , одна базисна, а інша – ні. Тоді, для такого розв’язку будуть використовуватись умови (13)-(17), а тому x за сор. вищ. Критерієм є оптимальним розв’язком задачі (10)-(12).

Також метод розв. зад. (10)-(12) назив. настр. степеня методом розв’язування цієї задачі.