1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.

Нехай маємо числову послідовність виду u, uq, uq²,..., uq^n-1,...

Таку послідовність, як відомо, називають нескінченною геометричною прогресією, а число q – знаменником прогресії.

Знайдемо суму S_n перших n членів прогресії. Таку суму можна знайти, бо в ній скінчене число доданків, а саме n, і вона дорівнює

S_n = u+uq+uq²+ . . . + uq^n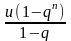-1= , якщо q≠1,

S_n= nu, якщо q=1.

Означення. Границя 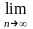S_n називається сумою нескінченної геометричної прогресії.

Знайдемо S_n. Для цього розглянемо такі випадки:

1) ׀q׀<1 : S_n= = ;

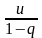2) ׀q׀>1 : S_n= = ;

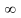3) q=1 : Тоді S_n = nu= ;

4)q=-1 : S_n=0, якщо n парне число, і S_n= u, якщо n- непарне число. Границя S_n не існує.

Отже, нескінченна геометрична прогресія має суму тільки тоді, коли ׀q׀<1, тобто коли вона є спадною. У цьому випадку записують

u+uq+uq²+ . . . + uq^n-1+ . . . = ;

Нехай маємо довільну числову послідовність a₁, a_{2 , . . . ,} a_n, . . .

Вираз виду a₁+ a₂ + . . . + a_n+ . . . (1) називають числовим рядом, або просто рядом. Числа a₁, a_{2 , . . . ,} a_n, ... називають членами ряду.

Для позначення ряду застосовують і такий символ:

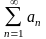= a₁+ a₂ + . . . + a_n+ . . .

Знайдемо суму перших n членів ряду S_n= a₁+ a₂ + . . . + a_n

Надаючи n значень 1,2,3 . . ., дістанемо таку числову послідовність:

S₁= a₁, S₂= a₁+ a_2, S₃= a₁+ a₂ + a_{3, . .,} S_n= a₁+ a₂ + . . . + a_{n, . . .}

_Числа S₁, S₂, S₃ , _{. . .}, _, S_n, . . .називають частиними сумами ряду (1). Означення. Скінчена границя послідовності { S_n } частинних сум називається сумою числового ряду (1).

S= S_n.

a₁+ a₂ + . . . + a_n+ . . . = S.

Означення. Числовий ряд (1) називається збіжним, якщо існує скінченна границя послідовності частинних сум і розбіжним в протилежному випадку.

Розглянемо ряд u+uq+uq²+ . . . + uq^n-1+ . . .

Цей ряд називається ще геометричним, а число q- знаменником ряду. Отже, при ׀q׀<1 геометричний ряд є збіжним, а при ׀q׀≥1 – розбіжним.

Додатні ряди. Ознаки збіжності

Числовий ряд = a₁+ a₂ + . . . + a_n+ . . . , (1) в якого всі члени є невід’ємні числа (a_n ≥ 0, n=1,2, . . . ), називають додатнім рядом.

Як і раніше, позначимо через S_n ( n=1,2, . . .) частині суми додатного ряду (1). Тоді, оскільки S_n+1= S_n + a_n+1 ≥ S_n ( n=1,2, . . .),

то послідовність { S_n }є неспадною. Така послідовність, згідно з теоремою про існування границі монотонної послідовності, збігається, якщо вона обмежена зверху, і розбігається, якщо вона не обмежена зверху.

Теорема 1. Для того, щоб додатній ряд (1) збігався, необхідно і достатньо, щоб послідовність його частинних сум { S_n } була обмеженою зверху.

Теорема 2. (ознака порівняння). Якщо члени додатних рядів

= a₁+ a₂ + . . . + a_n+ . . . , (А)

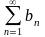= b₁+ b₂ + . . . + b_n+ . . . , (В)

починаючи з певного значення n, і для всіх наступних його значень (при n>N ) задовольняють нерівності a_n ≤ b_n ,

то із збіжності ряду (В) випливає збіжність ряду (А), а із розбіжності ряду (А), випливає розбіжність ряду (В).

Доведення: Не зменшуючи загальності, можна вважати, що нерівності a_n ≤ b_n виконуються для всіх n=1,2, . . .. Позначимо частинні суми ряду (А) через S_n , а частинні суми ряду (В) через S_n^’ . Тоді справджуються нерівності

S_n ≤ S_n^’ .

1⁰. Нехай ряд (В) збігається. Тоді послідовність { S_n^’ }, згідно з попередньою теоремою, обмежена зверху

S_n^’ < M, n=1,2, . . .

Проте тоді й S_n < M, n=1,2, . . .

Звідси і з попередньої теореми випливає, що ряд (А) збігається.

2⁰. Нехай ряд (А) розбігається. Тоді й ряд (В) розбігається, бо якби останній збігався, то за доведеним вище і ряд (А) збігався б. Теорему доведено.

Теорема 3. (ознака д’Аламбера). Якщо в ряді (1) a_n > 0 і існує границя = r, то при r<1 ряд (1) збігається, а при r>1 ряд (1) розбігається.

Доведення: Розглянемо випадок, коли r<1. Випадок, коли r>1, доводиться аналогічно.

Візьмемо число q таке, щоб r < q < 1. Тоді існує натуральне число N таке, що при всіх n > N виконується нерівність

< q, або а_n+1< a_n q, n > N.

Надаючи n значень N + 1,N + 2, . . . , матимемо такі нерівності:

a_N+2 < a_N+1 q, a_N+3 < a_N+1 q², a_N+4 < a_N+1 q³, . . ., a_N+k < a_N+1 q^k-1, . . .

Помічаємо, що члени числового додатного ряду (1), починаючи з N + 2, менші за відповідні члени ряду 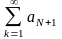q^к.

Останній ряд є збіжний як ряд, що є добутком числа a_N+1 і збіжного геометричного ряду. Тому і ряд (1) є збіжним.

Теорему доведено.

Теорема 4. (ознака Коші)_. Якщо в додатному ряді (1) існує границя

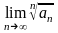_{= k , (2)}

то при k<1 ряд (1) збігається, а при k >1 ряд (1) розбігається.

Доведення: Розглянемо випадок, коли k<1. Випадок, коли k >1, доводиться аналогічно. Візьмемо число q таке, щоб справджувалися нерівності k < q < 1. Тоді існує число N таке, що при n > N виконуватиметься нерівність 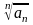< q, або а_n< qⁿ, n > N.

Отже, члени ряду (1), починаючи з a_N+1, менші за відповідні члени збіжного геометричного ряду 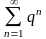, в якого знаменник q < 1. Тому й ряд (1) за ознакою порівняння є збіжним.

Теорему доведено.

Коли границя (2) існує і дорівнює 1, за ознакою Коші, як і за ознакою д’Аламбера, не можна встановити збіжність (розбіжність) ряду.

Теорема 5. (Інтегральна ознака Коші).

Якщо функція f(x) визначена в проміжку 1≤ х ≤ + і при х ≥ а ≥ 1 неперервна, додатна і спадна, то для того, щоб збігався числовий ряд

=f(1)+ f(2)+ . . . +f(n)+ . . . , (3)

Необхідно і достатньо, щоб збігався невласний інтеграл 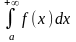(4)

Доведення: Розглянемо натуральні числа k, k+1, . . . ,k+n, . . . , де k ≥ a. Тоді на відрізку [k,k+1] функція, згідно з теоремою, спадає. Тому для x [k,k+1] справджуються нерівності

f(k+1) ≤ f(x) ≤ f(k).

Внаслідок відомої властивості визначеного інтеграла виконуються нерівності

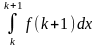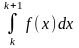≤ ≤ , або f(k+1) ≤ ≤ f(k)

Ці нерівності справедливі для будь–якого k = n, n+1, . . . , n+m, . . . Тому, надаючи k значень n, n+1, . . . , n+m, матимемо f(n+1) ≤ 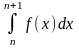≤ f(n), f(n+2) ≤ 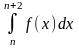≤ f(n+1), . . ., f(n+m+1) ≤ 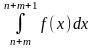≤ f(n+m).

Додамо почленно ці нерівності:

f(n+1) + f(n+2) + f(n+3) + . . .+ f(n+m+1) ≤ ≤

≤ f(n) + f(n+1) + . . . + f(n+m). (5)

З нерівностей (5) і випливає справедливість теореми.

Нехай невласний інтеграл (4) збігається. Тоді через те, що f(x) додатна при x ≥ a , < . Проте тоді

f(n+1)+f(n+2) + . . . + f(n+1+m) < .

У лівій частині останньої нерівності є m-та частинна сума n-го залишку ряду (3). Отже, ряд, що є n-м залишком ряду (3), збігається. Тому і ряд (3) збігається.

Нехай невласний інтеграл (4) розбігається. Тоді й ряд (3) розбігається. Припустимо супротивне. Нехай ряд (3) збігається. Тоді збігається й будь-який ряд, що є залишком ряду (3), зокрема ряд

f(n) + f(n+1) + . . . + f(n+m) + . . .

Послідовність частинних сум {S_m} цього ряду є обмеженою зверху, тобто S_m = f(n) + f(n+1) + . . . + f(n+m) < М.

Проте, згідно з нерівністю (5), < М.

Оскільки, f(x) > 0, то інтеграл при зростанні m монотонно зростає і є обмеженим зверху. Отже, існує границя

.

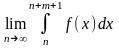Це означає, що невласний інтеграл (4) збігається, а ми припустили, що він розбігається. Отже, зайшли у суперечність.

Теорему доведено

Таким чином, ряд (3) і невласний інтеграл одночасно збігаються або розбігаються.