
- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
4.2. Метод мінімального елемента
Спочатку
вибирають у вхідній таблиці клітинку,
що відповідає найбільш дешевому маршруту,
для якої досягається
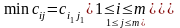 .
Покладаємо
.
Покладаємо
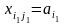 ,
якщо
,
якщо
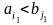 ,
та викреслюємо рядок з номером
,
та викреслюємо рядок з номером
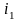 .
В цьому випадку змінюємо
.
В цьому випадку змінюємо
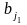 на
на
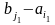 .
Якщо ж
.
Якщо ж
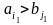 ,
то покладаємо
,
то покладаємо
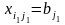 і викреслюємо стовпець з номером
і викреслюємо стовпець з номером
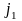 ,
замінивши при цьому
,
замінивши при цьому
 на
на
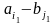 .
.
Якщо
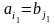 ,
то покладаємо
,
то покладаємо
 і викреслюємо або рядок з номером
,
або стовпець з номером
.
і викреслюємо або рядок з номером
,
або стовпець з номером
.
Якщо
викреслено стовпець, то замінивши
на
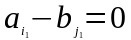 ;
якщо викреслимо рядок, то замінюємо
;
якщо викреслимо рядок, то замінюємо
 на
на
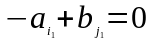 .
.
В кожному випадку отримується нова таблиця (нова трансформована задача), яку заповнюємо тим же методом мінімального елемента.
§5. Метод потенціалів розв’язування транспортної задачі.
Нехай маємо транспортну задачу. Побудуємо двоїсту для неї задачу, приписавши обмеженням (2) змінні u1,u2,u3, а обмеженням (3) – v1,v2,v3,v4 двоїстої задачі. Вона має вигляд
max w=a1u1+ a2u2+ a3u3+ b1u1+b2v2+ b3v3+ b4v4 (9)
при обмеженнях
u1+v1≤c11, u1+v2≤c12, u1+v3≤c13, u1+v4≤c14,
u2+v1≤c21, u2+v2≤c22, u2+v3≤c23, u2+v4≤c24, (10)
u3+v1≤c31, u2+v2≤c32, u3+v3≤c33, u3+v4≤c34.
Нехай маємо деякий базисний розв’язок задачі (1)-(4), отриманий, наприклад, методом північно-західного кута. Нехай, наприклад, його базисними змінними будуть х11, х12, х22, х23, х33, х34.
Складаємо систему рівнянь, яка отримується з (10), якщо замінити на = в тих, обмеженнях, які відповідають базисним змінним:
u1+v1≤c11, u1+v2≤c12, u2+v2≤c22, u2+v3≤c23, u3+v3≤c33, u3+v4≤c34. (11)
Алгоритму методу потенціалів розв’язування транспортної задачі (1) – (4):
1. Знаходимо вихідний базисний розв’язок (методом північно – західного кута або методом мінімальних елементів).
2. Розв’язуємо відповідну усьому базисному розв’язку систему рівнянь типу системи (11), яка одержується з обмежень задачі, двоїстої до (1) – (4) заміною знаків на в тих обмеженнях, у відповідність базисним змінним цього базисного розв’язку. В результаті знаходимо значення потенціалів ui , I = 1…m, та vj, j = 1…n.
3. Для всіх небазисних індексів (I, j) обчислюємо ij= ui + vj – cij. Якщо всі ці оцінки 0, то процес закінчено: розглядуваний базисний розв’язок є оптимальним. Якщо серед ij є > 0 , то за певним правилом вибираємо одну з цих оцінок (наприклад, найбільшу або першу із додатніх у порядку їх обчислення).
4. Будуємо новий базисний розв’язок, вводячи в число базисних змінних змінну хij , що відповідає вибраній симплекс – різниці ij > 0, і виводимо із числа базисних одну із старих базисних змінних.
Повертаємось до п. 2, маючи на увазі новий базисний розв’язок.
Білет 15
1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
Означення.
Метричним простором називається пара
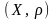 ,
що складається з деякої множини X
елементів і відстані, тобто однозначної,
невід'ємної, дійсної функції
,
що складається з деякої множини X
елементів і відстані, тобто однозначної,
невід'ємної, дійсної функції
 ,
визначеної для будь-яких х
і у з X,
і яка задовольняє таким трьом аксіомам:
,
визначеної для будь-яких х
і у з X,
і яка задовольняє таким трьом аксіомам:
1)
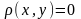 тоді і тільки тоді, коли
тоді і тільки тоді, коли
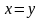 ;
;
2)
(аксіома симетрії):
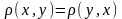 ;
;
3)
(аксіома трикутника):
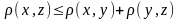 ;
;
Сам
метричний простір позначатимемо
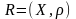 .
.
Приклади метричних просторів.
1. Множина упорядкованих груп з n дійсних чисел
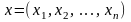 з
відстанню
з
відстанню 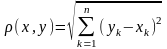 (1)
(1)
називається
– n-вимірним
арифметичним евклідовим простором
 Справедливість аксіом 1) і 2) для
Справедливість аксіом 1) і 2) для
 очевидна. Покажемо, що в
виконана й аксіома трикутника.
очевидна. Покажемо, що в
виконана й аксіома трикутника.
Нехай
 ,
,
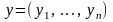 і
і
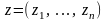 ;
тоді аксіому трикутника записуємо у
вигляді
;
тоді аксіому трикутника записуємо у
вигляді
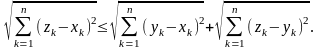 (2)
(2)
Припускаючи
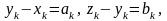 дістанемо
дістанемо
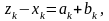 а нерівність (2) набуває при цьому вигляду
а нерівність (2) набуває при цьому вигляду
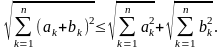 (3)
(3)
Але ця нерівність відразу випливає з відомої нерівності Коші-Буняковського:
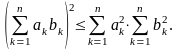 (4)
(4)
Справді, внаслідок цієї нерівності маємо
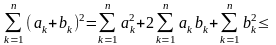
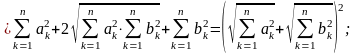
тим самим нерівність (3), а отже, і (2) доведено.
2. Множина С [a, b] усіх неперервних дійсних функцій, визначених на сегменті [a, b], з відстанню
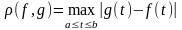 (5)
(5)
також утворює метричний простір. Аксіоми 1) – 3) перевіряємо безпосередньо. Цей простір відіграє дуже важливу роль в аналізі. Ми його позначатимемо тим самим символом С [a, b], що й множину точок цього простору. Замість С [0;1] ми писатимемо просто С.
Граничні точки. Замикання.
Відкритою
кулею
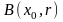 у метричному просторі
у метричному просторі
 ми називатимемо сукупність точок
ми називатимемо сукупність точок
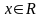 ,
які задовольняють умову
,
які задовольняють умову
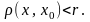
Точка
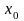 називається центром
цієї кулі, а число
називається центром
цієї кулі, а число
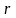 — її радіусом.
— її радіусом.
Замкнутою
кулею
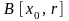 ми назвемо сукупність точок
,
які задовольняють умову
ми назвемо сукупність точок
,
які задовольняють умову
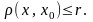
Відкриту
кулю радіуса
з центром
ми називатимемо також
-околом
точки
і позначатимемо символом
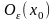 .
.
Точка
називається точкою
дотику
множини
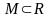 ,
якщо будь-який її окіл містить хоча б
одну точку з М.
Сукупність усіх точок дотику множини
М
позначається [M]
і називається замиканням
цієї множини.
,
якщо будь-який її окіл містить хоча б
одну точку з М.
Сукупність усіх точок дотику множини
М
позначається [M]
і називається замиканням
цієї множини.
Теорема 1 Операція замикання має такі властивості:
1)
 ,
,
2)
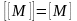 ,
,
3)
якщо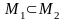 ,
то
,
то
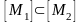 ,
,
4)
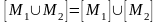 .
.
Доведення.
Доведемо,
наприклад, четверту властивість. Якщо
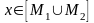 ,
то х
міститься
принаймні в одній з множин
,
то х
міститься
принаймні в одній з множин
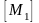 або
або
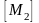 ,
тобто
,
тобто
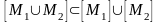 .
.
Оскільки
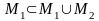 і
і
 ,
то обернене включення випливає з
властивості 3). Теорему доведено.
,
то обернене включення випливає з
властивості 3). Теорему доведено.
Точка називається граничною точкою множини , якою будь-який її окіл містить нескінченно багато точок з М.
Гранична точка може належати, а може не належати М. Наприклад, якщо М — множина раціональних чисел з відрізка [0,1], то кожна точка цього відрізка — гранична для M.
Точка
х,
яка належить М,
називається ізольованою
точкою
цієї множини, якщо в досить малому її
околі
 немає точок з M,
відмінних від х.
немає точок з M,
відмінних від х.
Усяка точка дотику множини М є або гранична, або ізольована точка цієї множини.
Замикання
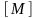 складається, взагалі кажучи, з точок
трьох типів:
складається, взагалі кажучи, з точок
трьох типів:
1) ізольовані точки множини М;
2) граничні точки множини M, які належать M;
3) граничні точки множини М, які не належать М.
Відкриті і замкнуті множини
Множина
М,
що лежить у метричному просторі
,
називається замкнутою,
якщо вона збігається з своїм замиканням:
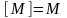 .
Інакше кажучи, множина називається
замкнутою, якщо вона містить всі свої
граничні точки.
.
Інакше кажучи, множина називається
замкнутою, якщо вона містить всі свої
граничні точки.
Приклади.
1.
Усякий сегмент
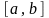 числової прямої є замкнута множина.
числової прямої є замкнута множина.
2.
Замкнута куля є замкнута множина.
Зокрема, у просторі
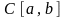 множина функцій f,
які задовольняють умову
множина функцій f,
які задовольняють умову
 ,
замкнута.
,
замкнута.
Теорема 2. Перетин будь-якого числа і сума будь-якого скінченного числа замкнутих множин є замкнуті множини.
Доведення.
Нехай
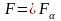 — перетин замкнутих множин
— перетин замкнутих множин
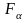 і нехай х
— гранична точка для F.
Це означає, що будь-який її окіл
має нескінченно багато точок з F.
Але тоді тим більше
має нескінченно багато точок з кожної
і, отже, бо всі
замкнуті, точка х
належить кожній
;
отже,
і нехай х
— гранична точка для F.
Це означає, що будь-який її окіл
має нескінченно багато точок з F.
Але тоді тим більше
має нескінченно багато точок з кожної
і, отже, бо всі
замкнуті, точка х
належить кожній
;
отже,
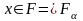 ,
тобто
,
тобто
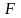 замкнута.
замкнута.
Нехай
тепер
— сума скінченного числа замкнутих
множин:
 ,
і нехай точка х
не належить
.
Покажемо, що х
не може бути граничною для
.
Справді, х
не належить жодній із замкнутих множин
,
і нехай точка х
не належить
.
Покажемо, що х
не може бути граничною для
.
Справді, х
не належить жодній із замкнутих множин
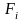 ,
отже, не є граничною ні для жодної з них.
Тому для кожного і
можна знайти такий окіл
,
отже, не є граничною ні для жодної з них.
Тому для кожного і
можна знайти такий окіл
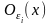 точки х,
яка має не більш як скінченне число з
.
Взявши з околів
точки х,
яка має не більш як скінченне число з
.
Взявши з околів
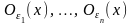 найменший, дістанемо окіл
точки х,
що містить не більш як скінченне число
точок з
.
найменший, дістанемо окіл
точки х,
що містить не більш як скінченне число
точок з
.
Отже, якщо точка х не належить , то вона не може бути граничною для , тобто замкнута. Теорему доведено.
Точка х називається внутрішньою точкою множини М, якщо існує окіл цієї точки, який цілком міститься в М.
Множина, всі точки якої внутрішні, називається відкритою.
Приклади.
1.
Інтервал
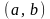 числової прямої
числової прямої
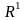 є відкрита множина; справді якщо,
є відкрита множина; справді якщо,
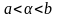 ,
то
,
то
 ,
де
,
де
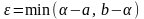 ,
повністю міститься в інтервалі
.
,
повністю міститься в інтервалі
.
2.
Відкрита куля
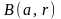 в будь-якому метричному просторі
є відкрита множина. Справді, якщо
в будь-якому метричному просторі
є відкрита множина. Справді, якщо
 ,
то
,
то
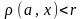 .
Припустимо, що
.
Припустимо, що
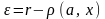 .
Тоді
.
Тоді
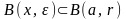 .
.
Теорема 3. Щоб множина М була відкрита, необхідно і достатньо, щоб її доповнення R\M до всього простору R було замкнуте.
Доведння. Якщо М відкрита, то кожна точка х з М має окіл, який повністю належить М, тобто такий що не має жодної спільної точки з R\M. Отже, жодна з точок, які не належать R \ M, не може бути точкою дотику для R \ M, тобто R \ M замкнуте. Навпаки, якщо R\M замкнуте, то будь-яка точка М має окіл, який повністю лежить в М, тобто М відкрита.
Оскільки порожня множина і всі R замкнуті і водночас є доповненнями одна одної, то порожня множина і всі R відкриті.
Теорема 4. Сума будь-якого числа і перетин будь-якого скінченого числа відкритих множин є відкриті множини.
