1. Інтерполювання функцій многочленами Лагранжа.

Постановка задачі

Вважають, що на множині дійсних чисел X визначено деяку дійс­­­ну функцію y=f(x), якщо кожному числу x з цієї множини пос­­тавлено у від­по­від­ність одне дійсне число y з множини Y. На прак­ти­ці часто трапляються випадки, коли формула задається склад­ним ви­разом і знайти значення y для відповід­них x досить важ­ко. Крім то­го, часто аналітичний вираз функ­ції y=f(x) вза­га­­лі невідомий, а ві­до­мі лише її значення в скінченій кіль­кості то­чок (функція задана таблично). Ці значення мо­жуть бути знай­де­ні в результаті спос­тережень чи ви­мі­рювань в яко­му-небудь екс­пе­рименті, або в ре­зультаті обчислень. Тому виникає пот­реба ви­хідну функцію y=f(x) наближе­но замінити (ап­рок­си­мува­ти) де­якою іншою функцією (x), в певному ро­зу­мінні близькою до f(x) і такою, що простіше обчислю­єть­ся чи дослід­жу­ється. Тоді при всіх зна­ченнях аргументу з множи­ни X покладають f(x)(x). Функ­­­цію (x) називають ап­рок­симую­чою. Близькість функцій f(x) і (x) можна, зок­рема, оцінювати в мет­ричних просторах за до­помо­гою відстані. По-різ­ному вводячи відс­тань, дістають різні конкретні випадки зада­чі апроксимації.

Часто апроксимуючу функцію (x) беруть у вигляді лінійної ком­бі­на­ції функцій деякого класу, які утворюють скінчену чи зчис­ленну мно­жину {_i(x)}, причому будь-яка скінчена система еле­ментів _i(x) лінійно не­за­лежна. Тобто (x) беруть у вигляді

(x) = ₀₀(x) +₁₁(x) + ... + _n_n(x), (1)

де – ₀, ₁,...,_n сталі коефіцієнти. Функцію (x) в цьому ви­пад­ку на­­зи­вають узагальненим многочле­ном. Надалі розглядатимемо наб­­ли­ження функцій узагальненими мно­го­членами.

Нехай у точках x₀, x₁, ... ,x_n (x_ix_j, якщо ij) з відрізка [a,b] відомі значення функції y=f(x): y₀=f(x₀), y₁=f(x₁),..., y_n=f(x_n). Роз­глянемо один з випадів апроксимації, що називається інтер­по­­лю­ван­ням, або інтерполяцією. Суть його полягає в тому, що кое­фі­ці­єн­ти ₀,₁,...,_n многочлена (1) добирають так, щоб у точ­ках x₀,x₁,...,x_n значення функ­цій f(x) і (x) збігалися, тобто

f(x_i)= (i=0,1,...,n) (2).

Точки x₀,x₁,...,x_n називаються вузлами інтерполювання, а мно­гоч­лен (x) – інтер­по­ля­ційним многочленом. Формулу y=(x), знай­­дену для обчислення зна­чень функції y=f(x), називають ін­тер­поляційною. Задача інтерполювання матиме єдиний роз­в’я­зок, якщо при будь-якому розміщенні вузлів визначник системи (2) не дорівню­вати­ме нулю, тобто

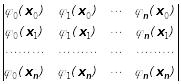0.

Системи функцій, які задовольняють таку умову, називають сис­­­темами Чебишова. На практиці систему {_i(x)} часто беруть у вигляді послідовності цілих невід’ємних степенів змінної x, тобто _i(x)=xⁱ (i=0,1,2,...). Тут узагальнені многочлени є звичайними алгебраїчними многочленами. Інтерполювання в цьому випадку називається по­ліноміальним, або параболіч­ним.

Інтерполяційний поліном Лагранжа

Нехай у точках x₀, x₁, ... , x_n (x_ix_j, якщо ij) з відрізка [a,b] задано значення функції y=f(x): y_i=f(x_i). Треба побудувати такий по­ліном L_n(x) = ₀+₁x+ ... +_nxⁿ (степеня, не вищого за n), який у вузлах x₀, x₁, ... , x_n набуває тих самих значень, що й функція y=f(x), тобто

L_n(x_i) = f(x_i) (i=0, 1, ... , n). (3)

З умови (3) для знаходження коефіцієнтів _i (i=0, 1, ... , n) діс­та­ємо систему рівнянь:

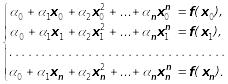(4)

Визначником цієї системи є визначник Ван дер Монда:

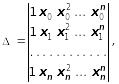
який, як відомо, дорівнює Це означає, що функції 1, x, x², ..., xⁿ утворюють систему Чебишева. Отже, сис­те­ма (4) має єдиний розв’язок при будь-яких значеннях f(x_i) (i=0, 1,...,n). Таким чином, коли серед вузлів немає таких, що збіга­ють­ся, то алгебраїчний многочлен існує і єдиний.

Щоб дістати інтерполяційний многочлен у явному вигляді, не ста­немо розв’язувати систему (4), а побудуємо безпосередньо мно­гоч­лен L_n(x), який задовольняє умову (3). Многочлен L_n(x) шу­ка­ти­мемо у вигляді лінійної комбінації деяких многочленів степеня n, причому коефіцієнтами цієї лінійної комбінації будуть задані зна­чення функції y=f(x) у вузлах, тобто

L_n(x)= (5)

де (x) (i=0, 1,..., n) – поки що невідомі многочлени степеня n.

З умо­ви (3) випливає, що многочлени (x) мають задо­воль­няти умо­­ву (x_j)= тобто

(x)= = .

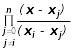Підставивши вирази (x) у формулу (5), дістанемо вираз ін­тер­­по­ля­ційного многочлена L_n(x):

L_n(x)= y_i (6)

Інтерполяційний многочлен, записаний у вигляді (6), назива­єть­ся інтерполяційним многочленом Лагранжа. Многочлени (x) на­зиваються коефіцієнтами Лагранжа.

Запишемо формулу Лагранжа для випадку рівновіддалених вуз­лів. Нехай x₁–x₀=x₂–x₁=...=x_n–x_n–1=h. Для спрощення зробимо за­міну x=x₀+th. Тоді x–x_k=h(t–k) і інтерполяційний поліном Лаг­ран­жа матиме вид:

L_n(x)= L_n(x₀+th)=t(t–1)(t–2)...(t–n) y_i , де t=(x–x₀)/h.

Оцінка похибки інтерполяційного многочлена Лагранжа

Побудований для функції y=f(x) інтерполяційний многочлен Лагранжа n-го степеня у вузлах інтерполювання x₀, x₁, ..., x_n збі­га­ється з функцією y=f(x). В інших точках відрізка [a,b] він від­різ­няється від функції y=f(x).

Величина R_n(x)=f(x)–L_n(x), яка характеризує близькість полі­но­­ма L_n(x) до функції f(x) у деякій точці відрізка [a,b], нази­вається залишковим членом інтерполяційного поліному Лаг­ран­жа. Знайдемо вираз для залишкового члена для функцій f(x), які на відрізку [a,b], що містить вузли інтерполювання, мають непе­рерв­ні похідні до (n+1)-го порядку включно.

Оскільки залишковий член у вузлах інтерполювання дорівнює нулю, то можна записати:

f(x)–L_n(x)=(x–x₀)(x–x₁)(x–x₂)...(x–x_n)k(x)=П_n+1(x)k(x), (7)

де k(x) – невідома функція. Для знаходження k(x) розглянемо до­по­міжну функцію u(t)=f(t)–L_n(t)–П_n+1(t)k(x), де x відіграє роль па­ра­метра. Тут за x візьмемо точку, в якій потрібно об­чис­лити за­лиш­ковий член інтерполяційного многочлена.

За рівністю (7) функція u(t) дорівнює нулю, якщо t=x₀, x₁,..., x_n і якщо t=x, тобто має на відрізку [a,b] принаймі n+2 нулі. От­же, на кін­цях кожного з відрізків [x₀;x₁], [x₁;x₂],...,[x_i;x], [x;x_i+1], ...,[x_n–1;x_n] функція u(t) набуває значень рівних нулю. За тео­ре­мою Ролля всередині кожного з цих відрізків знайдеться при­най­мі одна точка, яка буде нулем похідної u`(t). Отже похідна u`(t) має на відрізку [a,b] принаймі n+1 нуль. Міркуючи аналогічно, вста­­новлюємо, що u``(t) на [a,b] має принаймі n нулів. Нарешті, u⁽ⁿ⁺¹⁾(t) має на [a,b] принаймі один нуль : u⁽ⁿ⁺¹⁾()=0.

Оскільки (t)=0, =(n+1)!, то для u⁽ⁿ⁺¹⁾(t) маємо: u⁽ⁿ⁺¹⁾(t)=f⁽ⁿ⁺¹⁾(t)–(n+1)!k(x).

Отже, при t= дістаємо: 0=f⁽ⁿ⁺¹⁾()–(n+1)! k(x). Звідси k(x)=

Підставивши в рівність (7) значення k(x), дістанемо вираз для залишкового члена інтерполяційного многочлена L_n(x):

R_n(x)= П_n+1(x), (8)

де [a,b]. З формули (8) можна записати таку оцінку для R_n(x):

|R_n(x)|  |П_n+1(x)|, де M_n+1= |f⁽ⁿ⁺¹⁾(x)|.

У процесі обчислень виникають також неусувна похибка, ос­кіль­ки значення часто даються наближено, і похибка округлення про­міжних результатів. Останню можна звести до мінімуму, якщо обчислення виконувати з більшою кількістю цифр, ніж це вимагається для табличних значень функції. В остаточному результаті запасні цифри округлюють. Якщо оперувати усіма розрядами ЕОМ, то похибкою округлень проміжних результатів можна ігнорувати.