1. Означення детермінанта n-го порядку. Властивості детермінантів.

Детермінантом (визначником) n-го порядку, що відповідає матриці

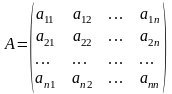
називається алгебраїчна сума n! членів складених таким чином: членами є всі можливі добутки елементів матриці, взятих по одному в кожному рядку і в кожному стовпці, причому член береться знаком плюс якщо його індекси утворюють парну підстановку і зі знаком плюс якщо його індекси утворюють парну підстановку і зі знаком мінус в противному випадку.

Детермінант n-го порядку позначають:

(1)

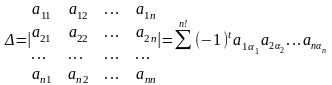
Назвемо транспонуванням матриці таке перетворення матриці при якому її рядки стають стовпцями з тими ж самими номерами. Матрицю, транспоновану до матриці А, позначимо через А′. Отже,

(3)

(2)

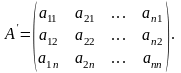
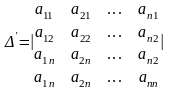
Властивість 1. Детермінант не зміниться при його транспонуванні.

Властивість 2. Якщо довільний з рядків (стовпців) складається з одних нулів, то детермінант дорівнює нулю.

Властивість 3. Від перестановки двох рядків (стовпців) детермінант змінює знак, а його абсолютна величина не зміниться.

Властивість 4. Детермінант, що має два однакові рядки (стовпці) дорівнює нулю.

Властивість 5. Якщо всі елементи деякого рядка (стовпця) детермінанта помножити на деяке число k, то сам детермінант множиться на k.

Властивість 6. Детермінант, що містить два пропорційних рядки (стовпці) дорівнює нулю.

Властивість 7. Якщо всі елементи i-го рядка детермінанта n-го порядку представлені у вигляді суми двох доданків 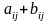, то детермінант дорівнює сумі двох детермінантів, в яких всі рядки, крім i-го такі як і в заданому детермінанті, а i-й рядок в одному з доданків складається з елементів , а в другому – з елементів .

Властивість 8. Детермінант не зміниться, якщо до елементів одного з його рядків (стовпців) додати відповідно елементи іншого рядка (стовпця), помноженого на деяке число.

2. Правила суми і добутку. Розміщення, перестанов­ки, комбінації (без повторень та з повтореннями).

Правило суми: якщо деякий об'єкт а можна вибрати n способами, а об'єкт b іншими т способами, то один з об'єктів а або b можна вибрати п+m способами.

Правило добутку, якщо об'єкт а можна вибрати п способами і при кожному виборі об'єкта а об'єкт b можна вибрати m способами, то вибір пари (а;b) можна здійснити пт способами.

Розміщенням без повторень з п елементів по k називають будь-яку впорядковану k -підмножину n - множини. Число розміщень з п елементів по k позначають символом . Перший елемент можна вибрати n способами, другий елемент - (n-1) способами, ..., останній елемент 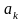- (n – k + 1) способами. Тому, згідно з узагальненим правилом добутку

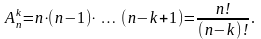
Перестановкою без повторень з n елементів називають розміщення з n елементів по n.

Число перестановок з n елементів позначають символом Р_n.

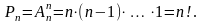
Комбінацією без повторень з n елементів по k називають будь-яку k- підмножину n- множини. Число комбінацій з n елементів по k позначають 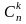. Розглянемо яку-небудь комбінацію. Впорядковуючи її всеможливими способами, отримаємо k! різних розміщень, тобто справедлива рівність

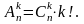
Отже, .

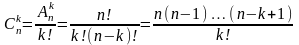Розміщенням з повтореннями з n елементів по k називається будь-яка впорядкована k -множина, утворена з елементів n - множини.

Число всіх розміщень з повтореннями з n елементів по k позначають через .

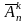Перший елемент розміщення можна вибрати n способами, другий елемент також n способами,..., останній елемент - n способами. Згідно з правилом добутку .

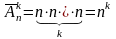Перестановкою з повтореннями з п елементів називається будь-яке впорядкування п-множини, серед елементів якої є однакові елементи.

Нехай серед елементів множини М є п₁ елементів 1-го типу, п₂ елементів 2-го типу п_к елементів к-типу (п₁+ п₂+…+ п_к= n). Число перестановок з елементів такої множини позначають Р_п(п₁, п₂,…, п_к). Має місце рівність Р_п(п₁, п₂,…, п_к) =

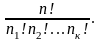
Комбінацією з повтореннями п елементів по k називається будь-яка к-множина, утворена з елементів заданої п-множини.

Число всіх комбінацій з повтореннями з п елементів по k позначають символом і обчислюють за формулою

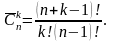
Білет 19

1. Розв’язування систем лінійних рівнянь методом Гауса.

Найбільш зручним для відшукання розв’язків систем лінійних рівнянь з числовими коефіцієнтами є метод послідовного виключення невідомих або метод Гауса.

Розглянемо систему лінійних рівнянь в загальному вигляді:

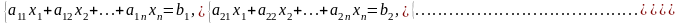(1)

Покладемо, для визначеності, а₁₁≠0, хоча може бути, що а₁₁=0 і ми повинні будемо почати з якого-небудь іншого, відмінного від нуля, коефіцієнта з першого рівняння системи.

Перетворимо систему (1), виключаючи невідоме х₁ з усіх рівнянь, крім першого. Для цього обидві частини першого рівняння помножимо на число і віднімемо від відповідних частин другого рівняння, потім обидві частини першого рівняння помножимо на число 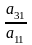віднімемо від відповідних частин третього рівняння і т.д.

Одержимо систему:

(2)

Система рівнянь (2) еквівалентна системі (1). Будемо перетворювати тепер систему (2). При цьому перше рівняння системи залишимо без зміни і перетворюватимемо лише частину системи, яка складається з усіх рівнянь крім першого. При цьому вважаємо, звичайно, що серед цих рівнянь немає таких, всі коефіцієнти лівих частин яких дорівнюють нулю, - такі рівняння ми відкинули б, якщо б їх праві частини дорівнювали нулю, а в противному разі довели б несумісність нашої системи. Таким чином, серед коефіцієнтів 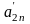є відмінні від нуля, для визначення приймемо, що

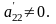
Перетворимо тепер систему (2) віднімаючи від обох частин третього і кожного з наступних рівнянь, обидві частини другого рівняння, помножені відповідно на числа

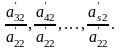
Цим буде виключено невідоме х₂ з усіх рівнянь, крім першого та другого, і прийдемо до системи рівнянь, еквівалентної системі (2), а тому й системі (1):

(3)

Наша система містить тепер t рівнянь, t≤s, оскільки деякі рівняння виявились, можливо, відкинутими.

В подальшому перетворенні підлягає лише частина системи, яка містить всі рівняння, крім двох перших.

Коли закінчиться цей процес послідовних перетворень?

Якщо ми прийдемо до такої системи, одне з рівнянь якої має відмінний від нуля вільний член, а всі коефіцієнти лівої частини дорівнюють нулю, то, як ми знаємо, наша вихідна система несумісна.

В протилежному випадку ми одержимо таку систему рівнянь, еквівалентну (1):

(4)

Тут

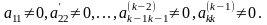
Відмітимо також, що k≤s, і очевидно, k≤n.

В цьому випадку система (1) сумісна. Вона буде визначена при k=n. Дійсно, якщо k=n, то система (4) має вигляд

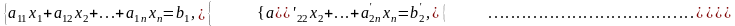(5)

З останнього рівняння легко одержати невідоме 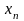_. Підставляючи його в передостаннє рівняння знайдемо значення x_n-1. Продовжуючи процес далі знайдемо, що система (5), а тому і система (1) має єдиний розв’язок, тобто сумісна та визначена.

Якщо k≤n, то для всіх “вільних” невідомих x_k+1,…x_n візьмемо довільні числові значення, після чого рухаючись по системі (4) знизу вгору, ми як і раніше знайдемо для невідомих 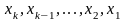цілком визначенні значення. Оскільки значення для вільних невідомих можна вибрати нескінченним числом способів , т система (4) і, як наслідок, система (1) будуть сумісними, але невизначеними. Легко переконатись в тому, що так будуть знайдені всі розв’язки системи (1).

Зауважимо, що трикутна форма системи (5) одержалась завдяки припущенню, що коефіцієнти a₁₁,a₂₂ і т.д. відмінні від нуля. В загальному випадку, таку систему можна одержати лише після зміни, належним чином, нумерації.

При практичному розв’язуванні системи лінійних рівнянь методом Гаусса потрібно виписати матрицю з коефіцієнтів системи, приєднати до неї стовпець з вільних членів, для зручності відокремлений горизонтальною рискою, а всі перетворення виконувати над рядками цієї розширеної матриці. Зауважимо, що можна прийти і до ступінчатої матриці.