
- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
Об’єм тіла обертання
Візьмемо криволінійну трапецію aABb, обмежену графіком функції y= f(x), неперервної і невід’ємної на відрізку [a; b], віссю Ох і прямими x=a і x=b.
Цю криволінійну трапецію, як тверде тіло, обертатимемо навколо осі Ох. При цьому криволінійна трапеція опише деяке тіло, яке називається тілом обертання.
Візьмемо (T)- розбиття відрізка [a; b],
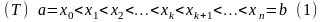
Позначимо
через
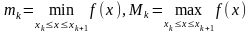 (k=0,1,2,…,n-1).
(k=0,1,2,…,n-1).
Розглянемо
прямокутники
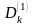 і
і
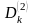 ,
основами яких є відрізок [
]
і
,
основами яких є відрізок [
]
і
висоти
яких відповідно дорівнюють
 (k=0,1,2,…,n-1).При
обертанні криволінійної трапеції aABb
навколо осі Ох
і прямокутники
і
(k=0,1,2,…,n-1),
кожний з яких опише прямий коловий
циліндр.
(k=0,1,2,…,n-1).При
обертанні криволінійної трапеції aABb
навколо осі Ох
і прямокутники
і
(k=0,1,2,…,n-1),
кожний з яких опише прямий коловий
циліндр.
Позначимо
через
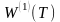 тіло, яке складається з
прямих колових циліндрів, описаних
прямокутниками
(k=0,1,2,…,n-1),
а через
тіло, яке складається з
прямих колових циліндрів, описаних
прямокутниками
(k=0,1,2,…,n-1),
а через
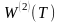 -
тіло, що складається з
прямих колових циліндрів, описаних
прямокутниками
(k=0,1,2,…,n-1). Легко помітити, що тіло
цілком міститься в тілі
-
тіло, що складається з
прямих колових циліндрів, описаних
прямокутниками
(k=0,1,2,…,n-1). Легко помітити, що тіло
цілком міститься в тілі
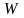 ,
утвореному обертанням навколо осі Ох
криволінійної трапеції aABb,
а тіло
само цілком містить у собі це тіло
.
,
утвореному обертанням навколо осі Ох
криволінійної трапеції aABb,
а тіло
само цілком містить у собі це тіло
.
Об’єми
прямих колових циліндрів, утворених
обертанням навколо осі Ох прямокутників
і
,
дорівнюють відповідно
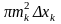 і
і
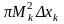 ,
тому
,
тому
Об’єм
=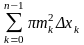 ,
об’єм
=
,
об’єм
=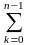 .(2)
.(2)
Обємом
тіла обертання
називається спільна границя (якщо вона
існує), до якої прямують об’єми тіл
і
при
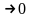 ,
тобто спільна границя сум (2).
,
тобто спільна границя сум (2).
Суми
(2) є відповідно нижньою і верхньою сумами
Дарбу, складеними для функції
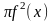 і (T)-
розбиття(1) відрізка [a; b]. Оскільки f(x)-
неперервна функція на відрізку [a; b], то
на цьому відрізку буде неперервною, а
отже, і інтегрованою і функція
.
Тому при
суми
(2) (а отже, і об’єми тіл
і
)
прямуватимуть до однієї й тієї ж границі
V, що дорівнює визначеному інтегралу
і (T)-
розбиття(1) відрізка [a; b]. Оскільки f(x)-
неперервна функція на відрізку [a; b], то
на цьому відрізку буде неперервною, а
отже, і інтегрованою і функція
.
Тому при
суми
(2) (а отже, і об’єми тіл
і
)
прямуватимуть до однієї й тієї ж границі
V, що дорівнює визначеному інтегралу
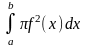 .
.
Таким
чином, об’єм
V
тіла
,
утвореного
обертанням навколо осі Ох криволінійної
трапеції aABb,
обчислюється
за формулою :
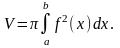
Площа поверхні обертання
Нехай
спрямлювана крива АВ
задана рівняннями

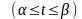 (1),де
(1),де
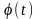 і
—функції, неперервні разом з своїми
похідними першого порядку на відрізку
,
причому
і
—функції, неперервні разом з своїми
похідними першого порядку на відрізку
,
причому
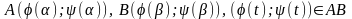 для
для
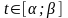
і
кожним двом різним значенням
(за винятком, можливо, значень
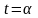 і
і
 )
відповідають дві різні точки кривої
АВ.
Візьмемо довільну фіксовану точку
і € [а; р] і їй відповідну точку
)
відповідають дві різні точки кривої
АВ.
Візьмемо довільну фіксовану точку
і € [а; р] і їй відповідну точку
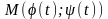 на кривій АВ.
Довжина дуги АМ
дорівнює
на кривій АВ.
Довжина дуги АМ
дорівнює
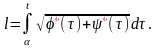
Ясно,
що l(t)
— неперервна монотонно зростаюча
функція на відрізку [0;
L],
де
—
довжина
всієї кривої АВ.
Така функція має обернену. Позначимо
її через
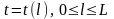 .
Функція
.
Функція
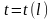 неперервна на відрізку [0;
L].
Підставивши цю функцію в рівняння кривої
(1), дістанемо
неперервна на відрізку [0;
L].
Підставивши цю функцію в рівняння кривої
(1), дістанемо
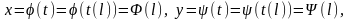 (2)
(2)
де
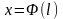 і
і
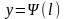 —
неперервні функції від l
на відрізку [0;
L].
Ми дістали параметричні рівняння (2)
кривої АВ,
в яких роль параметра виконує l
— довжина дуги АМ.
Скористаємось цими рівняннями для
знаходження площі поверхні, утвореної
обертанням кривої АВ
навколо осі Ох
на 360°.
—
неперервні функції від l
на відрізку [0;
L].
Ми дістали параметричні рівняння (2)
кривої АВ,
в яких роль параметра виконує l
— довжина дуги АМ.
Скористаємось цими рівняннями для
знаходження площі поверхні, утвореної
обертанням кривої АВ
навколо осі Ох
на 360°.
Для цього візьмемо (Т) - розбиття відрізка [0; L]:
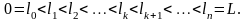 (3)
(3)
Позначимо
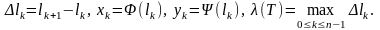
З'єднавши
точки
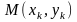 послідовно відрізками
послідовно відрізками
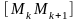 ,
дістанемо вписану ламану лінію
,
дістанемо вписану ламану лінію
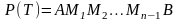 .
Позначимо через
.
Позначимо через
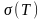 площу поверхні, утвореної обертанням
навколо осі Ох
на 360° цієї ламаної.
площу поверхні, утвореної обертанням
навколо осі Ох
на 360° цієї ламаної.
Площею
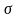 поверхні,
утвореної обертанням кривої АВ
навколо осі Ох
на 360°, називається границя при
площі
поверхні,
утвореної при цьому обертанні
вписаної ламаної P(T),
тобто
поверхні,
утвореної обертанням кривої АВ
навколо осі Ох
на 360°, називається границя при
площі
поверхні,
утвореної при цьому обертанні
вписаної ламаної P(T),
тобто
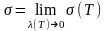 (4)
(4)
Позначимо
через
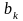 довжину відрізка
(рис. 61).
довжину відрізка
(рис. 61).
При обертанні навколо осі Ох вписаної ламаної відрізок
при цьому опише зрізаний конус, площа бокової поверхні якого
дорівнює
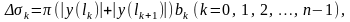 звідси
звідси
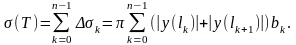 (5)
(5)
Треба
знайти границю суми (5) при
.
Проте ця сума не є інтегральною, оскільки
,
взагалі кажучи, не є
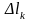 .
Перетворимо суму (5) так, щоб границю
перетвореної суми можна було легко
знайти. Маємо:
.
Перетворимо суму (5) так, щоб границю
перетвореної суми можна було легко
знайти. Маємо:
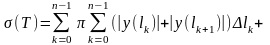
 (6)
(6)
Суми
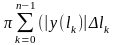 і
і
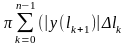 ,
будучи інтегральними сумами, складеними
для неперервної функції
,
будучи інтегральними сумами, складеними
для неперервної функції
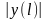 і (Т)
- розбиття (3) відрізка [0;
L],
при
прямують до границі, що дорівнює
і (Т)
- розбиття (3) відрізка [0;
L],
при
прямують до границі, що дорівнює
 .
Таким чином,
.
Таким чином,
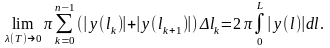 (7)
(7)
Покажемо,
що границя при
другої
суми, яка стоїть у правій частині рівності
(6), дорівнює нулю. Дійсно, функція
,
будучи неперервною на відрізку [0,
L],
обмежена на цьому відрізку:
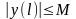 .
Отже,
.
Отже,
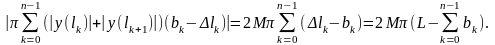 (8)
(8)
Оскільки
крива AВ
cпрямлювана,
то при
довжина вписаної ламаної P(Т),
що дорівнює
 ,
прямує до довжини L
кривої АВ.
Звідси і з (8) випливає, що границя другої
суми, яка стоїть у правій частині рівності
(6), дорівнює нулю. З (4), (6) і (7) маємо
,
прямує до довжини L
кривої АВ.
Звідси і з (8) випливає, що границя другої
суми, яка стоїть у правій частині рівності
(6), дорівнює нулю. З (4), (6) і (7) маємо
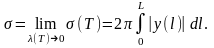 (9)
(9)
За цією формулою і обчислюють площу поверхні, утвореної обертанням навколо осі Ох на 360° спрямлюваної кривої АВ.
Якщо крива АВ задана рівняннями (1), де і — функції, неперервні разом із своїми похідними першого порядку на відрізку , то площа поверхні обертання визначається за формулою
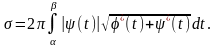 (10)
(10)
Дійсно, формула (10) виходить з формули (9) за допомогою підстановки.
Якщо
крива АВ
в декартових прямокутних координатах
задана рівнянням
,
де
—
функція,
неперервна разом із своєю похідною
першого порядку на відрізку [а;
b],
то площу поверхні обертання обчислюють
за формулою
 яка є окремим випадком формули (10).
яка є окремим випадком формули (10).
2. Лінійне програмування (ЛП). Приклади задач лінійного програмування (ЗЛП). Загальна та канонічна форми запису ЗЛП. Ознака оптимальності базисного допустимого розв’язку ЗЛП. Ознака необмеженості цільової функції ЗЛП на допустимій множині. Симплекс-метод розв’язування ЗЛП.
Лінійне програмування (ЛП).
Однією
з найважливіших задач оптимізації є
задача математичного програмування,
що полягає у відшуканні найбільшого
або найменшого значення функції f(x)
при обмеженнях
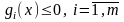 ,
,
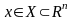 .
.
Якщо
функції f(x),
,
- лінійні, а область Х задається лінійними
обмеженнями вигляду
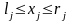 ,
зокрема,
,
зокрема,
 ,
,
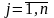 ,
то така задача математичного програмування
називається задачею лінійного
програмування (ЗЛП).
,
то така задача математичного програмування
називається задачею лінійного
програмування (ЗЛП).
Приклади задач лінійного програмування.
