2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.

1) Методи відшукання початкового базисного розв’язку

Нехай маємо ЗЛП, записану у канонічній формі (КЗЛП):

Знайти (1)

за умов

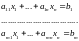(2)

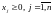, (3)

де m<n та серед векторів умов цієї задачі є m лінійно залежних.

Будемо вважати, що b_i≥0, 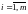, (цього можна домогтися множенням, при потребі, відповідних рівнянь системи (2) на -1).

Ставиться питання про відшукання початкового базисного розв’язку.

1. Описання методу штучного базису відшукання початкового базисного розв’язку.

Розв’язуємо допоміжну КЗЛП:

Знайти 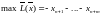(4)

за умов

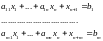(5)

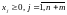. (6)

Зауважимо, що змінні x_n+1,…,x_n+m називаються штучними. Відповідні їм вектори умов 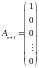, , 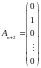…, 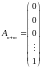є лінійно не залежними. Зрозуміло, що тоді вектор 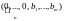є початковим базисним розв’язком задачі (4) – (6).

Тому можна розв’язувати цю задачу симплекс-методом. Оскільки x_n+1≥0, … x_n+m≥0 то можливі два випадки:

1. найбільше значення цільової функції 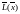за умов (5) – (6) дорівнює 0;

2. найбільше значення цільової функції за умов (5) – (6) менше 0.

В першому випадку оптимальний базисний розв’язок 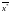задачі (4) – (6) має вигляд: .

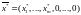При цьому 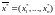– базисний розв’язок ЗЛП (1)–(3).

В другому випадку область допустимих значень ЗЛП (1)–(3) D = .

Зауважимо, що коли деяке рівняння системи (5) містить змінну з коефіцієнтом 1, яка відсутня в інших рівняннях цієї системи, то не має сенсу вводити штучну змінну. Її роль відіграватиме змінна, про яку йде мова.

Застосування методу штучного базису приводить до того, що задачу (1)–(3) доведеться розв’язувати за два етапи: спочатку розв’язується задача (4)–(6), а потім (1)–(3).

2) Описання м-методу розв’язування злп.

Нехай маємо ЗЛП (1)-(3), в якій як і вище, . Розглянемо таку допоміжну 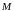-задачу лінійного програмування:

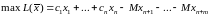(7)

(8)

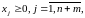(9)

де мислиться як завгодно великим додатним числом.

Першим базисним розв’язком цієї задачі є вектор .

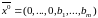Розв’язуючи цю задачу симплекс методом, одержимо один з трьох випадків:

1. в оптимальному розв’язку 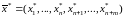-задачі всі ;

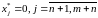2. в 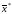принаймні одна з компонент більша нуля;

3. -задача розв’язку немає (функція 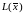необмежена зверху на множині, що визначається обмеженнями (8), (9)).

Можна переконатися, що в цих випадках відповідно маємо:

1. оптимальний розв’язок задачі (1)-(3) має вигляд ;

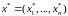2. ЗЛП (1)-(3) не має допустимих розв’язків ( );

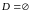3. ЗЛП (1)-(3) розв’язку не має ( 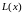необмежена зверху на множині допустимих розв’язків цієї задачі (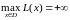 ) або ).

Білет 13

1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.

Числовий ряд виду 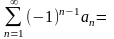a₁ – a₂ + a₃ – a₄ + ... + (-1)^n-1a_n + ... (1), в якому числа a_n додатні (a_n > 0, n=1,2, . . .) називають знакозмінним рядом.

Теорема (Лейбніца).

Якщо в знакозмінному ряді (1) числа a_n монотонно не зростають a_n+1 ≤ a_{n ,} n=1,2, . . . (2) a_n = 0, (3), то такий ряд збігається.

Доведення: Частинні суми ряду (1) позначимо через S_n. Тоді, поклавши n=2m ( m=1,2, . . .), дістанемо S_2m = (a₁ - a₂) + (a₃ – a₄) + ... + (a_2m-1 – a_2n). (4)

Кожна різниця в круглій дужці правої частини останньої рівності є число, згідно з нерівністю (2), невід’ємне. Тому послідовність { S_2m } є монотонно неспадна. Запишемо рівність (4) в такому вигляді:

S_2m = a₁ – (a₂ – a₃ ) + (a₃ – a₄ )+ . . . + (a_2m-2 – a_2m-1 ) – a_2m .

Звідси із нерівності (2) випливає, що S_2m ≤ a₁. (5)

Отже, послідовність частинних сум { S_2m } парного порядку, будучи неспадною і обмеженою зверху, збігається. Позначимо 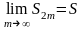(6)

Розглянемо тепер частинні суми ряду (1) непарного порядку, тобто S_2m-1. Тоді S_2m-1 можна записати в такому вигляді:

S_2m-1= S_2m + a_2m .

Перейдемо до границі при 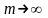. Згідно з рівностями (3) і (6), дістаємо

.

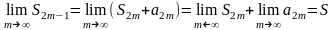Таким чином, послідовність парних і непарних частинних сум збігається до того самого числа S. А це означає, що ряд (1) є збіжний і його сума дорівнює числу S.

Теорему доведено.

Перейдемо в нерівності (5) до границі при m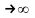 . Маємо S ≤ a_1. (7)

Отже, якщо ряд (1) задовольняє умовам теореми Лейбніца, то такий ряд збігається і його сума не перевищує величини першого члена цього ряду.

Запишемо n–й залишок ряду (1)

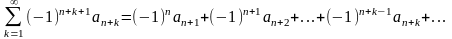(8)

Розглянемо знакозмінний ряд (9)

Нехай ряд (1) задовольняє умовам теореми Лейбніца. Тоді й ряд (9) задовольняє умовам теореми Лейбніца. Отже, ряд (9) збігається і його сума r^’_n, згідно з нерівністю (7), не перевищує величини першого члена

r_n^’ ≤ а_n+1 (10)

Суму ряду (8) можна записати у вигляді

r_n = (-1)ⁿ r_n^’ (11)

Звідси і з нерівності (10) дістаємо, що 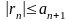. (12)

Наслідок (з теореми Лейбніца).

Якщо знакозмінний ряд (1) задовольняє умовам теореми Лейбніца, то n – й залишок його має знак свого першого члена і за модулем не перевищує модуля цього члена.

Абсолютно та умовно збіжні ряди. Властивості збіжних рядів.

Нехай маємо числовий ряд 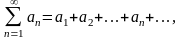(1)

в якому члени а_n (n=1,2, . . .) є довільні дійсні числа.

Означення 1. Ряд (1) називають абсолютно збіжним, якщо збігається числовий ряд, утворений з модулів членів даного ряду

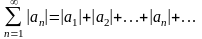(2)

Означення 2. Числовий ряд (1) називається умовно (або не абсолютно)збіжним, якщо цей ряд збігається, а складений для нього ряд (2) розбігається.

Критерій Коші збіжності числового ряду.

Для того, щоб збігався числовий ряд (1), необхідно й достатньо, щоб для будь-якого числа існувало натуральне число N = N(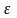 ) таке, що для всіх n > N і будь-якого натурального числа p = 1,2, . . . виконувалася нерівність

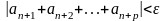. (5)

Справді, позначимо через { S_n } послідовність частинних сум ряду (1) і застосуємо до неї критерій Коші збіжності числової послідовності. Тоді для збіжності послідовності { S_n } необхідно і достатньо, щоб для будь-якого існувало натуральне число N = N( ) таке, щоб для всіх n > N і m>N виконувалася нерівність .

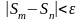Поклавши в цій нерівності m=n + p ( p=1, 2, … ), дістанемо нерівність (5).

Теорема 1. (Коші ). Якщо числовий ряд (1) абсолютно збіжний, то він є збіжний.

Доведення: Якщо ряд (2) збігається, то для нього виконується нерівність (5), яка в цьому випадку має вигляд

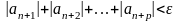(6)

для всіх n > N і будь-якого p=1, 2, …

Використовуючи властивість модуля суми, маємо

.

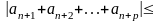Теорему доведено.

Сформулюємо (без доведення) у вигляді теорем властивості збіжних числових рядів.

Теорема 2. ( Сполучна властивість). Якщо збігається ряд (1), то збігається й ряд 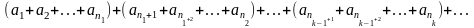, (7)

Причому, він має ту саму суму, що й ряд (1).

Теорема 3. (Переставна властивість). Якщо числовий ряд (1) абсолютно збіжний, то ряд, складений перестановкою членів ряду (1), збігається і має ту саму суму, що й ряд (1).