
- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
Неперервною
плоскою кривою
називається сукупність точок у площині,
координати яких х
і у
є функції
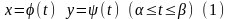 параметра, неперервні на відрізку
параметра, неперервні на відрізку
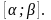
Візьмемо
(T)–розбиття
відрізка
: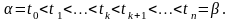
Позначимо
через

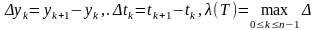 .Довжина
k-ї ланки
.Довжина
k-ї ланки
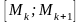 вписаної ламаної
вписаної ламаної
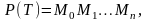 дорівнює
дорівнює
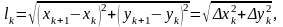
Тому
довжина L(T)
ламаної P(T)
запишеться так

Якщо
довжина L(T)
вписаної ламаної P(T) незалежно від
взятого (T)-розбиття
залишається обмеженою
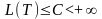 (4), то неперервна крива називається
спямлюваною,
а число
(4), то неперервна крива називається
спямлюваною,
а число
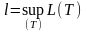 називається довжиною
цієї кривої.
Якщо існують такі (T)-розбиття
відрізка
,
що довжини
називається довжиною
цієї кривої.
Якщо існують такі (T)-розбиття
відрізка
,
що довжини
 як завгодно великі, то неперервна крива
називається неспрямлюваною.
як завгодно великі, то неперервна крива
називається неспрямлюваною.
Теорема
(Жордана).Для
того щоб неперервна крива (1) була
спрямлю-ваною, необхідно і достатньо,
щоб
 були функціями з обмеженими варіаціями
на відрізку
були функціями з обмеженими варіаціями
на відрізку
Доведення.
Необхідність. Нехай неперервна крива (1) спрямлювана. Для довільного (T)- розбиття (2) відрізка маємо
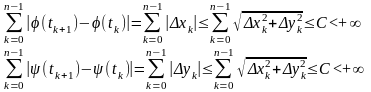
А це означає, що функції з обмеженими варіаціями на відрізку
Достатність. Нехай - функція з обмеженими варіаціями на відрізку Тоді для довільного (T)- розбиття цього відрізка маємо
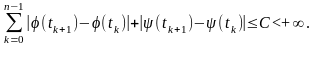
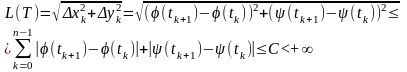
Крива (1) є спрямлювана.
Наслідок. Для того щоб крива, задана в прямокутних декартових координатах рівнянням y=f(x), f(x) – неперервна функція на відрізку [a; b], була спямлюваною, необхідно і досить, щоб f(x) була функцією з обмеженою варіацією на відрізку [a; b].
Означення:
Неперервна
крива (1) називається спрямлюваною,
якщо при
існує
скінченна границя довжин L(T)
вписаних ламаних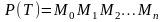 .
.
Теорема 2. Для того щоб неперервна крива (1) була спрямлюваною, необхідно і достатньо, щоб існувала скінченна границя
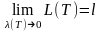
Ця границя дорівнює довжині l спрямлюваної кривої.
Неперервна
крива (1) називається гладкою,
якщо функції
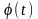 і
і
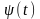 мають похідні
мають похідні
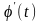 і
і
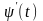 ,
неперервні на відрізку
,
неперервні на відрізку
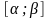 ,
які одночасно не перетворюються в нуль
,
які одночасно не перетворюються в нуль
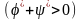 .
.
Неперервна
крива (1) називається кусково–гладкою,
якщо вона складається з скінченного
числа гладких кривих. Довжина спрямлюваної
гладкої кривої (1) визначається за
формулою 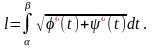 (19)
(19)
За теоремою Лагранжа маємо
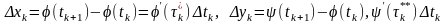
тому
довжину
вписаної ламаної
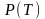 запишемо так:
запишемо так:
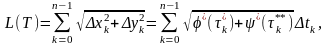 (20)
(20)
де
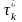 і
і
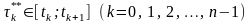 .
.
Довжина
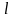 кривої (1) дорівнює границі сум (20) при
кривої (1) дорівнює границі сум (20) при
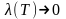 .
Однак суми (20) не є інтегральними, оскільки
точки
і
.
Однак суми (20) не є інтегральними, оскільки
точки
і
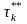 різні.
різні.
Щоб
знайти границю суми (20), до цієї суми
додамо і віднімемо суму
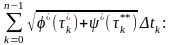
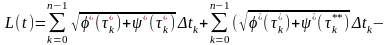
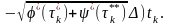 (21)
(21)
Перша
сума в рівності (21) є інтегральною сумою,
складеною для функції
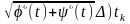 і
і
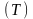 -розбиття
(2) відрізка
.
Оскільки функції
і
неперервні на відрізку
,
то на цьому відрізку неперервна (а отже,
й інтегровна) і функція
-розбиття
(2) відрізка
.
Оскільки функції
і
неперервні на відрізку
,
то на цьому відрізку неперервна (а отже,
й інтегровна) і функція
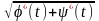 .
.
Тому
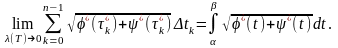 (22)
(22)
Покажемо, що границя другої суми в рівності (21) при дорівнює нулю.
Задамося
числом
.
Оскільки функція
неперервна
на відрізку
,
то, за теоремою Кантора, вона рівномірно
неперервна на цьому відрізку. Тому для
числа
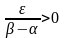 знайдеться число
таке, що
знайдеться число
таке, що
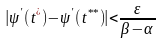 для
для
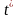 і
і
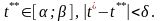
Візьмемо
-
розбиття (2), для якого
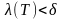 .
.
Тоді
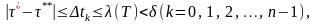
тому
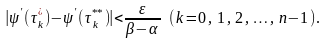 (23)
(23)
Скориставшись
нерівністю
 для оцінки зверху кожного
доданка
другої суми в рівності (21) і
застосувавши
нерівність (23), дістанемо
для оцінки зверху кожного
доданка
другої суми в рівності (21) і
застосувавши
нерівність (23), дістанемо
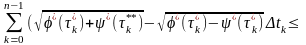
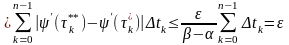
і, отже, при границя другої суми в рівності (21) дорівнює нулю. Перейшовши до границі при в рівності (21), дістанемо формулу (19) для обчислення довжини кривої (1).
Покажемо, що формула (19) залишається правильною і для обчислення довжини кусково- гладкої кривої.
Справді,
якщо неперервна крива (1) кусково-гладка,
то її можна розбити на скінченне число
гладких кривих. Це означає, що відрізок
можна зобразити у вигляді суми скінченного
числа відрізків
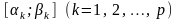 ,
попарно без спільних внутрішніх точок:
,
попарно без спільних внутрішніх точок:
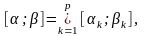
де
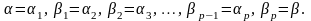
На
кожному відрізку
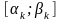 функції
і
мають неперервні похідні
і
,
якщо під значенням цих похідних у точках
функції
і
мають неперервні похідні
і
,
якщо під значенням цих похідних у точках
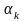 і
і
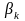 розуміти однобічні похідні. Таким чином,
функції
і
обмежені на відрізку
і можуть мати розриви першого роду
тільки в точках
і
розуміти однобічні похідні. Таким чином,
функції
і
обмежені на відрізку
і можуть мати розриви першого роду
тільки в точках
і
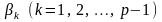 .
Цю властивість має і функція
.
Тому ця функція інтегровна за Ріманом
на відрізку
і внаслідок адитивної властивості
інтеграла Рімана правильна рівність
.
Цю властивість має і функція
.
Тому ця функція інтегровна за Ріманом
на відрізку
і внаслідок адитивної властивості
інтеграла Рімана правильна рівність
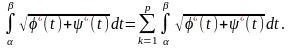
За
адитивною властивістю спрямлюваної
кривої кусково-гладка крива спрямлювана
і її довжина дорівнює сумі довжин
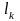 кривих, відповідних відрізкам
:
кривих, відповідних відрізкам
:
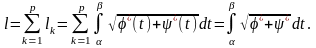
Отже, довжина l кусково-гладкої кривої (1) також обчислюється за формулою (19).
Нехай
крива АВ
в
полярних координатах задана рівнянням
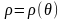 ,
де
,
де
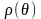 —
невід'ємна функція, неперервна разом
із своєю похідною першого порядку на
відрізку
—
невід'ємна функція, неперервна разом
із своєю похідною першого порядку на
відрізку
 ,
причому
,
причому
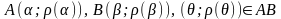 для
для
 і кожним двом різним значенням
і кожним двом різним значенням
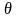 (за винятком, можливо, значень
(за винятком, можливо, значень
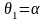 і
і
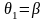 )
відповідають дві різні точки кривої
АВ.
Використовуючи зв'язок між декартовими
і полярними координатами
)
відповідають дві різні точки кривої
АВ.
Використовуючи зв'язок між декартовими
і полярними координатами
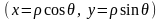 ,
параметричні рівняння (1) кривої АВ
запишемо в такому вигляді:
,
параметричні рівняння (1) кривої АВ
запишемо в такому вигляді:

Роль
параметра t
тут виконує кут
.
Оскільки
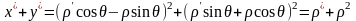 ,
то:
,
то:
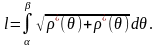 (24)
(24)
Якщо
крива АВ
в декартових координатах задана рівнянням
 ,
де
,
де
 — функція, неперервна разом з своєю
похідною першого порядку на відрізку
— функція, неперервна разом з своєю
похідною першого порядку на відрізку
 ,
то, взявши х
за параметр t,
параметричні рівняння (1) кривої
АВ запишемо у вигляді:
,
то, взявши х
за параметр t,
параметричні рівняння (1) кривої
АВ запишемо у вигляді:

Формула
(19) для
і
цього
випадку набуде вигляду:
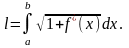 (25)
(25)
Білет11
