
- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
Лінійним диф. рівнянням першого порядку наз. рівняння вигляду
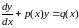 , (1)
, (1)
де функції p(x) і q(x) неперервні в інтервалі (а; b). Якщо функція q(x) тотожно дорівнює нулю в інтервалі (а; b), то рівняння (1), яке має вигляд
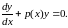 (2)
(2)
називається
однорідним.
Якщо ж q(x)
 0
(a
< x < b),
то воно називається неоднорідним.
0
(a
< x < b),
то воно називається неоднорідним.
Загальний розв’язок однорідного рівняння
1)
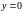
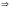 — розв’язок.
— розв’язок.
2)
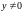
Шукаємо розв’язки, відмінні від нуля.
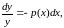 (3)
(3)
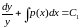 ,
,
звідки
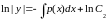 (С2
>
0)
(С2
>
0)
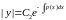
і, нарешті,
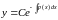 . (4)
. (4)
Загальний розв’язок неоднорідного рівняння (метод Бернуллі)
Згідно з методом Бернуллі розв'язок рівняння (2) шукаємо у вигляді
y(x) = u(x) v(x), (5)
де и(х) і v(x) — невідомі функції. Надалі припускатимемо, що функції и(х) та v(x) неперервні разом із своїми похідними першого порядку в інтервалі (а; b). Знаходячи
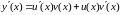
і підставляючи це значення і функцію у(х) в рівняння (2), дістаємо таку рівність:
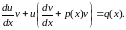 (6)
(6)
Виберемо функцію v(x) так, щоб
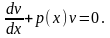
Оскільки останнє рівняння є лінійним однорідним, то
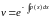 ;
;
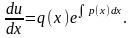 ;
;
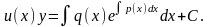
Підставляючи знайдене значення функцій и(х) та v(x) у формулу (5), дістаємо загальний розв'язок рівняння (2):
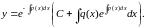 (7)
(7)
Рівняння Бернуллі
До рівнянь, які зводяться до лінійного диференціального рівняння, належить так зване рівняння Бернуллі
y' + p(x)y = q(x)y". (8)
У рівнянні (8) р(х) і q(x) неперервні на проміжку (a; b), a n — деяке дійсне число.
При
п
=
0
або п
= 1 рівняння (8) є лінійним рівнянням,
загальний розв'язок якого був знайдений
вище. Тому надалі припускатимемо, що п
0,
п
1
і у
0.
Помноживши обидві частини рівняння (8)
на
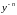 ,
дістанемо
,
дістанемо
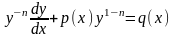 . (9);
. (9);
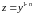 .(10);
.(10);
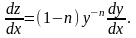
Помноживши обидві частини диференціального рівняння (9) на (1-п), матимемо лінійне диференціальне рівняння:
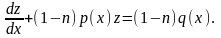
Визначивши з цього рівняння функцію z і підставивши її в (10), знайдемо шукану функцію у:
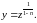
Ми
знайшли загальний розв'язок рівняння
Бернуллі (8) припустивши, що
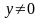 .
Функція
.
Функція
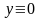 також є розв'язком рівняння (8), у чому
можна переконатись безпосередньою
перевіркою.
також є розв'язком рівняння (8), у чому
можна переконатись безпосередньою
перевіркою.
Рівняння в повних диференціалах
Нехай
функції
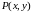 і
і
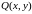 визначені і неперервні в однозв’язній
області D
площини
визначені і неперервні в однозв’язній
області D
площини
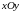 і в жодній точці цієї області не
перетворюються одночасно в нуль.
і в жодній точці цієї області не
перетворюються одночасно в нуль.
Рівняння вигляду
 (1)
(1)
називається
рівнянням у повних диференціалах, якщо
його ліва частина в області D
є повний диференціал деякої функції
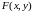 .
.
Рівняння (1) можна записати у вигляді
 (2)
(2)
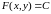 — загальний
інтеграл рівняння (1).
— загальний
інтеграл рівняння (1).
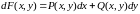 . (3)
. (3)
Нехай
функції
і
неперервні разом з частинними похідними
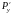 і
і
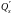 в однозв’язній області D
площини
.
в однозв’язній області D
площини
.
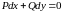 , (4)
, (4)
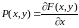 ,
,
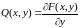 (5);
(5);
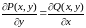 ,(6)
,(6)
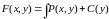 ,
,
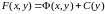 (7);
(7);
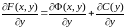 (8)
(8)
Використавши (5), одержимо
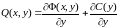 . (9)
. (9)
Знаходимо C за допомогою інтегрування. Знайшовши її, підставляємо у (7), одержуємо функцію , приривнявши яку до C, маємо загальний розв’язок рівняння (1).
2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
Означення 1. Булевою називається функція, яка, як і її аргументи, набувають значень лише 0 або 1.
Задати булеву функцію можна таблицею істинності або логічною формулою.
Якщо булева функція залежить від багатьох змінних, то задавати і досліджувати її зручніше не таблицею істинності, а аналітично (формулою). При цьому намагаються формулу звести до однієї з канонічних форм.
Означення 2. Елементарною кон’юнкцією називається кон’юнкція пропозиційних змінних та їх заперечень.
Означення 3. Елементарною диз’юнкцією називається диз’юнкція пропозиційних змінних та їх заперечень.
Число
пропозиційних змінних в елементарній
кон’юнкції (диз’юнкції) називають її
рангом. Наприклад,
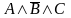 – елементарна кон’юнкція рангу 3;
– елементарна кон’юнкція рангу 3;
 – елементарна диз’юнкція рангу 4.
Пропозиційну змінну А
можна
вважати як елементарною кон’юнкцією,
так і диз’юнкцією рангу 1. Формула
– елементарна диз’юнкція рангу 4.
Пропозиційну змінну А
можна
вважати як елементарною кон’юнкцією,
так і диз’юнкцією рангу 1. Формула
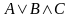 не є ні елементарною кон’юнкцією, ні
диз’юнкцією.
не є ні елементарною кон’юнкцією, ні
диз’юнкцією.
Означення 4. Диз’юнкція n елементарних кон’юнкцій називається n-членною диз’юнктивною нормальною формою. Скорочений запис відповідно днф.
Означення 5. Кон’юнкція n елементарних диз’юнкцій називається n-членною кон’юнктивною нормальною формою. Скорочений запис відповідно кнф.
Наприклад,
формула
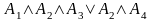 є 2-членною днф, а формула
є 2-членною днф, а формула
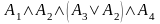 є 4-членною кнф.
є 4-членною кнф.
Розглянуті вище нормальні форми не визначаються однозначно для заданої формули: для тієї самої булевої функції існують істотно різні кнф і днф (звичайно, всі вони рівносильні між собою). Виділимо з класу нормальних форм для даної формули алгебри висловлень певний підклас, члени якого однозначно визначаються за даною формулою (з точністю до порядку запису). Введемо ряд означень.
Означення 6. Елементарна кон’юнкція (диз’юнкція) називається правильною, якщо кожна пропозиційна змінна входить до неї не більше ніж один раз, включаючи також входження змінної під знаком заперечення.
Наприклад,
елементарна кон’юнкція
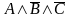 є правильною, а елементарна
диз’юнкція
є правильною, а елементарна
диз’юнкція
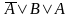 не є правильною.
не є правильною.
Означення
7. Елементарна
кон’юнкція (диз’юнкція) називається
повною щодо пропозиційних змінних
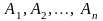 ,
якщо кожна з цих змінних входить до неї
хоча б один раз (або із знаком заперечення,
або без нього).
,
якщо кожна з цих змінних входить до неї
хоча б один раз (або із знаком заперечення,
або без нього).
Так,
щодо змінних
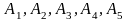 елементарна диз’юнкція
елементарна диз’юнкція
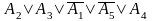 є повною, а елементарна кон’юнкція
є повною, а елементарна кон’юнкція
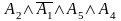 не є повною.
не є повною.
Означення 8. Досконалою диз’юнктивною нормальною формою (позначається Дднф) щодо пропозиційних змінних називається диз’юнктивна нормальна форма, кожна елементарна кон’юнкція якої є правильною і повною щодо даного набору пропозиційних змінних.
Означення 9. Досконалою кон’юнктивною нормальною формою (позначається Дкнф) щодо пропозиційних змінних називається кон’юнктивна нормальна форма, кожна елементарна диз’юнкція якої є правильною і повною щодо даного набору пропозиційних змінних.
Так,
днф
 не є Дднф щодо змінних
не є Дднф щодо змінних
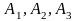 ,
бо вона містить елементарну кон’юнкцію
,
бо вона містить елементарну кон’юнкцію
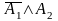 ,
яка не є повною (не містить змінної
,
яка не є повною (не містить змінної
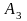 ).
Так само, не є Дднф і формула
).
Так само, не є Дднф і формула
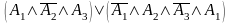 ,
оскільки друга елементарна кон’юнкція
в ній не є правильною (змінна
входить до неї двічі). Навпаки, днф
,
оскільки друга елементарна кон’юнкція
в ній не є правильною (змінна
входить до неї двічі). Навпаки, днф
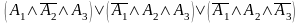 є досконалою щодо
тих
самих пропозиційних змінних. Прикладом
Дкнф щодо пропозиційних змінних
може служити формула
є досконалою щодо
тих
самих пропозиційних змінних. Прикладом
Дкнф щодо пропозиційних змінних
може служити формула
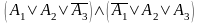 .
.
Будь-яку булеву функцію, відмінну від тотожного нуля, можна подати у вигляді Дднф. Справедливість цього встановлюється за допомогою наступного алгоритму:
Позбутися операцій еквіваленції та імплікації, якщо вони є, використовуючи рівносильності
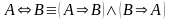 і
і
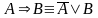 .
.
За допомогою правил де Моргана та властивості подвійного заперечення отримати формулу, в якій кожний символ заперечення стосується лише однієї пропозиційної змінної.
Використовуючи рівносильність
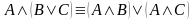 ,
перетворити вираз у днф.
,
перетворити вираз у днф.Кожну неправильну елементарну кон’юнкцію перетворити в правильну, використовуючи комутативну і асоціативну властивості, властивість суперечності та рівносильності
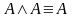 ,
,
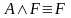 і
і
 .
.До неповної елементарної кон’юнкції, яка не містить, наприклад, змінної
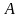 ,
приєднати кон’юнктивно тавтологію і
замінити її виразом
,
приєднати кон’юнктивно тавтологію і
замінити її виразом
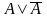 .
Після цього розкрити дужки за
дистрибутивною властивістю. У разі
необхідності цей процес повторювати
доти, поки кожна неповна елементарна
кон’юнкція не перетвориться в повну.
.
Після цього розкрити дужки за
дистрибутивною властивістю. У разі
необхідності цей процес повторювати
доти, поки кожна неповна елементарна
кон’юнкція не перетвориться в повну.Якщо в остаточній формулі є однакові диз’юнктивні члени, то залишити тільки один з них.
Дане представлення єдине (з точністю до порядку членів).
Будь-яку булеву функцію, відмінну від тотожної одиниці, можна подати у вигляді Дкнф, яка є єдиною (з точністю до порядку членів).
Алгоритм зведення подібний до попереднього:
Позбутися операцій еквіваленції та імплікації.
За допомогою правил де Моргана та властивості подвійного заперечення отримати формулу, в якій кожний символ заперечення стосується лише однієї пропозиційної змінної.
Використовуючи рівносильність
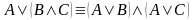 ,
перетворити вираз у кнф.
,
перетворити вираз у кнф.Кожну неправильну елементарну диз’юнкцію перетворити в правильну, використовуючи комутативну і асоціативну властивості, властивість виключеного третього та рівносильності
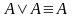 ,
,
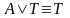 і
і
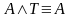 .
.До неповної елементарної диз’юнкції, яка не містить, наприклад, змінної A, приєднати диз’юнктивно фальш і замінити її виразом
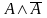 .
Після цього застосувати дистрибутивну
властивість. У разі необхідності
цей процес повторюється, як і у випадку
зведення до Дднф.
.
Після цього застосувати дистрибутивну
властивість. У разі необхідності
цей процес повторюється, як і у випадку
зведення до Дднф.
Якщо в остаточній формулі є однакові кон’юнктивні члени, то залишити тільки один з них.
Досконалі диз’юнктивні або кон’юнктивні нормальні форми є логічним виразом, що складається з пропозиційних змінних і трьох логічних операцій: диз’юнкції, кон’юнкції і заперечення. Кожна пропозиційна змінна може приймати значення 0 або 1, тобто також є булевою функцією. Множину булевих функцій, пов’язаних між собою операціями диз’юнкції, кон’юнкції і заперечення, називають булевою алгеброю або алгеброю Буля.
Якщо розглядати лише дві операції, суму Жегалкіна і кон’юнкцію, то одержимо іншу алгебру, яку називають алгеброю Жегалкіна. Тобто алгебра Жегалкіна – це множина булевих функцій, пов’язаних між собою кон’юнкцією та сумою Жегалкіна.
Алгебра Жегалкіна заслужила особливу увагу завдяки так званим досконалим поліноміальним нормальним формам (Дпнф), які ще називають поліномами Жегалкіна. Будь-яку булеву функцію можна єдиним способом подати у вигляді поліному Жегалкіна.
Поліноми Жегалкіна – це елементарні кон’юнкції і тавтологія, пов’язані між собою сумою Жегалкіна.
Наприклад,
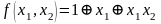 .
.
Білет25
