1.Еліпс, означення та канонічне рівняння. Досліджен­ня форми еліпса за канонічним рівнянням.

Еліпсом називається множина всіх точок площини. Для кожної з яких сума відстаней до двох заданих точок, які називаються фокусами, є величина стала, більша за відстань між фокусами.

Позначимо через F₁ і F₂ фокуси еліпса. Введемо Декартові систему координат так, щоб вісь х проходила через фокуси, а вісь у ділила відрізок F₁F₂ навпіл (рис.1). Позначимо відстань між фокусами через 2с. Тоді координати точок F₂(-с,0) і F₁(с,0).

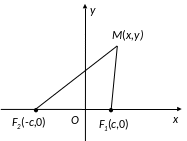Нехай М(х, у) – довільна точка еліпса. Довжини відрізків F₂M i F₁M, позначимо відповідно r₂ i r₁. Сума цих відстаней дорівнює деякій сталій, що характеризує даний еліпс. Цю сталу позначимо через 2а. З означення еліпса випливає, що а>c.

Маємо:

(1)

,

.

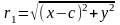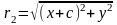(2)

За означенням еліпса

.

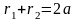Використовуючи (1) і (2), одержуємо для координат довільної точки еліпса рівняння

(3)

.

.

.

.

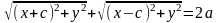
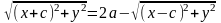
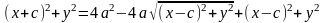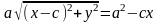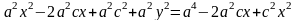(4)

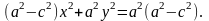
Покладемо 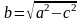. Це можливо, оскільки a>c. Очевидно, що a>b>0. Рівняння (4) можна записати так: 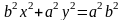або

(5)

.

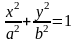В процесі спрощення рівняння (3) ми двічі підносили його до квадрату і могли одержати рівняння не еквівалентне даному, тобто окрім точок еліпса, рівнянню (5) могли би задовольняти координати точок, які не належать еліпсові. Можна довести, що рівняння (3) і (5) еквівалентні і як наслідок ніяких точок, що не лежать на еліпсові рівняння (5) не визначає. Рівняння (5) називається канонічним рівнянням еліпса. Зауважимо, що канонічне рівняння еліпса одержується в спеціально вибраній Декартові системі координат.

З рівняння (5) випливає 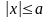і .

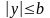2. Матрична гра. Оптимальні чисті стратегії. Критерії існування розв’язку матричної гри у чистих стратегіях. Оптимальні змішані стратегії та їх відшукання за допомогою ЛП. Існування розв’язку матричної гри у змішаних стратегіях (теорема про мінімакс).

Матрична гра.

Матрична гра визначається такими правилами. Грають два гравці P1 та P2. Перший з них вибирає число (стратегію) i (i=1,...,m), другий — число j (j=1,...,n). Вибiр гравці роблять одночасно i незалежно один від одного. Пiсля цього гравець P1 платить P2 суму , що визначається умовами конкретної гри (якщо >0, то P1 платить P2, якщо <0, то P2 платить P1 суму | |). Величини , i=1,...,m, j=1,...,n, відомі кожному з гравців. Потрiбно вказати найкращий вибір для кожного гравця.

Розглянемо матрицю

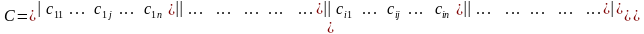
i назвемо її платіжною матрицею або матрицею виграшів гравця P2. Очевидно, що вибір числа i гравцем P1 можна трактувати, як вибір i-го рядка матриці С, вибір числа j гравцем P2, як вибір j-го стовпця тієї ж матриці.

Зауважимо, що якщо позначити через I та J відповідно множини можливих стратегій гравців P1 та P2, тобто I={1,...,i,...,m}, J={1,...,j,...,n}, то матрична гра повністю визначається трійкою G = (I,J,C).

Оптимальні чисті стратегії

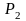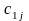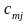Розглянемо матричну гру G з точки зору гравця . Нагадаємо, що він вибирає j-й стовпець ( ,..., )' матриці C. При цьому він одержує від першого гравця принаймні

Оскiльки гравець прагне зробити свій виграш максимальним i може довільно вибирати стовпець матриці C, то він вибирає j таким, що максимiзує

При цьому гарантований виграш дорівнює величині

(1)

що називається нижньою ціною гри G.

Аналогiчним чином можна розглянути цю ж гру з точки зору гравця 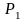. Зрозумiло, що матрицею його виграшів є матриця –C=||– ||, i=1,...,m, j=1,...,n. Мiркуючи аналогічно, робимо висновок, що гарантований виграш гравця складає

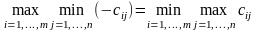
При цьому гравець одержить щонайбільше

(2)

Величина 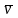називається верхньою ціною гри G.

Отже, гравець може гарантувати собі виграш принаймні 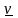, а гравець може перешкодити йому одержати більше . Якщо v = = , тобто

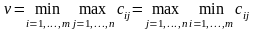(3)

то гравець має зрозуміти, що він може одержати v, а його супротивник перешкодить йому одержати більше v. Тому числа i*, j* такі, що у співвідношенні (5.3) c_i*j*=v, природно назвати оптимальними чистими стратегіями гравців та відповідно. У цьому випадку кажуть, що матрична гра G допускає розв'язок у чистих стратегіях, а величина v називається ціною гри.

Виявляється, що співвідношення (3) виконується далеко не для кожної гри, що визначається платіжною матрицею С. Отже, не кожна гра має розв'язок у чистих стратегіях.

Вияснимо загальні умови, при яких має місце співвідношення (3). Нехай f(x,y) — дійсна функція дійсних змінних x є X, y є Y.

Означення 1. Точка (x*,y*) називається сiдловою точкою функції f(x,y), якщо для будь-яких x є X, y є Y має місце нерівність

f(x*,y) ≤ f(x*,y*) ≤ f(x,y*). (4)

Як частинний випадок маємо: сiдловою точкою матриці C = || ||, i=1,...,m, j=1,...,n, називається пара (i*,j*) така, що

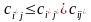(5)

для всіх i=1,...,m та j=1,...,n.

Кажуть, що матрична гра має сiдлову точку, якщо сiдлову точку має її платіжна матриця.

Теорема 1. Матрична гра G має розв'язок у чистих стратегіях тоді i лише тоді, коли її платіжна матриця С має сiдлову точку. При цьому, якщо (i*,j*) — сiдлова точка матриці C, то ціна гри .

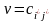Доведення цієї теореми безпосередньо випливає з двох лем, що розглядаються нижче.

Лема 5.1. Нехай для дійсної функції f(x,y), x є X, y є Y, існують

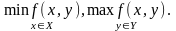
Тоді має місце нерівність

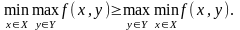(6)

Лема 5.2. Нехай виконані умови леми 1. Для того, щоб виконувалось співвідношення

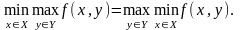(7)

необхідно i достатньо, щоб функція f(x,y) мала сiдлову точку. При цьому для сiдлової точки (x*,y*)

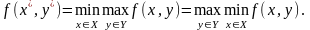(8)