- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
Задача
про швидкість рухомої точки.
Нехай точка М
рухається
по прямій за законом S=S(t),
де
S
— довжина
шляху, взята від деякої початкової точки
Мо,
t час,
за який
пройденошлях
S.
Нехайа
М — положення
точки в момент t
(рис
33),а М’ – в момент часу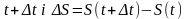 -
довжина
шляху, пройденого за час
-
довжина
шляху, пройденого за час
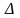 t.
Відношення
t.
Відношення
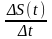
в
механіці називається величиною середньої
швидкості руху на ділянці
 ,
а границя цього відношення при
,
а границя цього відношення при
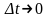 називається величиною
швидкості руху в точці М,
або
величиною миттєвої швидкості в момент
t.
Якщо
величину миттьової швидкості в момент
t
позначити
через V
(t),
то
називається величиною
швидкості руху в точці М,
або
величиною миттєвої швидкості в момент
t.
Якщо
величину миттьової швидкості в момент
t
позначити
через V
(t),
то
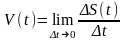
Таким
чином, для знаходження величини миттьової
швидкості в момент t
треба
обчислювати границю (2)
відношення
приросту шляху S(t)
в
момент t
за
часом, протягом якого цей приріст шляху
стався при умові, що час прямує до нуля.
Іншими словами, й тут треба знайти
границю відношення приросту функції
S(t)
в
точці t
до
приросту аргументу і,
коли
приріст аргументу
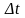 прямує до нуля.
прямує до нуля.
Можна навести ряд інших задач, в яких доводиться находити границю відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
3.
Означення
похідної.
Нехай
функція у
=
f(x)
означена в деякому околі точки х0
і нехай х—
точка
з цього околу,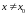 .
Якщо
відношення
.
Якщо
відношення
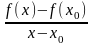
має
границю при
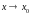 ,
то ця границя називається похідною
функції
,
то ця границя називається похідною
функції
 (х)
в
точці х0
і позначається
(х)
в
точці х0
і позначається
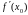 Таким
чином,
Таким
чином,
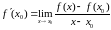
Якщо
ввести позначення
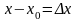 ,
то означення похідної запишемо у вигляді
,
то означення похідної запишемо у вигляді
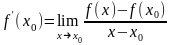
або у вигляді
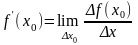
тобто похідною функції f(х) в точці х0 називається границя відношення приросту функції f(х) в точці х0 до приросту аргументу, коли приріст аргументу прямує до нуля. Рівність (1) тепер можна записати так:
 (4)
(4)
тобто похідна функції f(х) в точці х„ дорівнює тангенсу кута нахилу дотичної до кривої у — f(x) в точці (х0; f (x0)) з додатним напрямом осі Ох. Це твердження виражає геометричний зміст похідної.
Рівність (2), яку можна переписати у вигляді
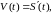 (5)
(5)
переконує нас у тому, що величина миттьової швидкості в момент часу t дорівнює похідній від шляху до часу. Це твердження виражає механічний зміст похідної.
2. Величини. Концепція типів даних у мові програмування.
Програма в Сі записується символами алфавіту, який містить: великі й малі букви латинського алфавіту;
десяткові цифри 0, 1, ..., 9;
спеціальні символи . " , [ ] ( ) { } + – / % \ ; : ? < = > — | ~ ^ & * #, символ пропуску _ тощо.
Із символів складаються базові елементи мови з певним самостійним значенням — лексичні одиниці (лексеми). В Сі є шість типів лексем: ідентифікатори, ключові слова, константи, рядки, роздільники та знаки операцій. Скрізь у тексті програми між двома лексемами можна записати коментар — довільну послідовність символів, обмежену символами /* і */, причому в самому коментарі цих символів немає.
Ідентифікатор — це послідовність букв, цифр і символів підкреслення, яка починається з букви. Ідентифікатори вживаються для іменування різних об’єктів: змінних, констант, функцій тощо. Довжина ідентифікаторів довільна, відрізняються вони, як правило, тільки за першими кількома символами. В залежності від конкретної реалізації ідентифікатори імен зовнішніх об’єктів, зокрема функцій, мають не більше 6—8 символів.
Ряд ідентифікаторів вживається для побудови конструкцій мови: вони називаються ключовими словами і мають фіксоване значення. Це такі ідентифікатори:
позначення типів даних
char int union double
long unsigned enum short
float struct void typedef
позначення класів пам’яті
auto extern register static
позначення операторів та їхніх складових частин
break case continue default
do else for goto
If return switch while
Вживаються константи трьох арифметичних типів: символьні, цілі, з плаваючою крапкою (плаваючі). Рядки записуються як послідовності символів у лапках " ". Ім’я функції, за яким у дужках ( ) записані її аргументи, називається покажчиком функції. З констант, імен змінних і покажчиків функцій за допомогою знаків операцій будуються вирази — правила обчислення та зміни значень об’єктів програми. Зміна значень задається виразами присвоювання.
Оператори присвоювання і введення — виведення забезпечують передачу і зміну інформації в пам’яті ЕОМ та на зовнішніх носіях; оператори керування позначають порядок виконання дій.
Описи характеризують класи пам’яті та типи іменованих об’єктів — змінних і функцій. З описів і операторів будуються найбільші конструкції мови — блоки та функції.
Організація програми.
Програма являє собою одну або кілька функцій, команд препроцесора і зовнішніх описів. Функції описують сукупності дій; команди препроцесора вказують на перетворення, яким потрібно піддати програму; зовнішні описи характеризують її дані. Одна з функцій має ім’я main() є головною, з неї починається виконання роботи. Програма може розміщуватись у кількох частинах – файлах, поєднаних між собою препроцесором відповідно до його команд. Імена файлів записуються з символом ‘.’.
Розглянемо просту програму друку на екрані фрази "Hello world"
#include "conio.h"
main() // програма
{
printf("Hello world \n");
getch();
}
Розглянемо структуру програми
Cі– програма |
|
|
|
|
# Директиви препроцесора |
|
|
|
|
|
|
|
Main |
|
|
|
|
|
|
|
|
Оператори |
|
|
|
|
|
|
|
|
|
|
Функція 1( ) |
|
|
|
|
|
|
|
|
Оператори |
|
|
|
|
|
|
Функція n ( ) |
|
|
|
|
|
|
|
|
Оператори |
|
|
|
|
Описи |
|
|
|
Привласнення |
|
|
|
Функції |
|
|
|
Управління |
|
|
|
Порожні |
Команда #include підключає файл conio.h до нашої програми. У файлі міститься інформація про функції робот из консоллю.
Символ # вказує, що перш ніж транслювати програму необхідно включити в неї функції з файлу conio.h - це так звана препроцесорна обробка, яка здійснює деяку попередню обробку тексту програми перед початком компіляції.
Рядок main() містить назву функції, з якою завжди починається програма. Порожні дужки означають, що ця функції, але вона без параметрів.
Після символів // розташовують коментарі (для одного рядка) (коментарями також називаються символи, що стоять між /* та */).
Фігурні дужки { відзначають початок і кінець тіла програми або функції. Вони також застосовуються для об'єднання декількох операторів програми в блок.
У рядку printf ("Hello world\n") міститься стандартна функція друку Сі. Рядок символів, заключений в дужки (аргумент) є інформацією, що передається функції printf() з нашої головної функції main(). Коли виконання функції буде завершено, управління повернеться назад в початкову програму. Символ \n - позначає переклад рядка на новий рядок після друку. Функція getch() дозволяє затримати зображення на екрані очікуючи натиснення будь-якої клавіші. Після цього програма завершує свою роботу. У файлі <stdio.h> міститься інформація про функції введення виведення.
При роботі в середовищі VisualStudio замість <stdio.h> необхідно підключати заголовочний файл <stdafx.h>!
Приклад.
# include <stdafx.h>
main ()
{
int a;
printf (“введіть число \n”);
scanf (“%d”, &a);
printf (“число а=%d”, a);
}
Скалярні дані
Базові типи даних.
Тип даних визначається певною множиною значень об'єктів та сукупністю дій, які можна виконувати над цими об'єктами. Об'єкти поділяються на скалярні, які в певному розумінні є неподільні, та структурні, що є скінченною сукупністю скалярних
Скалярні дані поділяються на кілька базових типів: символьні, цілі, плаваючі (або з плаваючою крапкою), беззнакові; ці типи називаються арифметичними. Типи, їхні імена та розмір пам'яті в байтах, яку займають дані цих типів у більшості ЕОМ, наведені в табл. 1. Байт пам'яті — це послідовність з восьми бітів (розрядів), кожний з яки може мати значення 0 чи 1, тобто байт може мати 28 = 256 неоднакових станів.
Діапазон цілих, що займають 2 байти, від —32768 до 32767; що займають 4 байти, від –231 до 231 – 1; відповідні діапазони беззнакових цілих – від 0 до 65535 і від 0 до 232 – 1. Плаваючі числа за абсолютним значенням у більшості ЕОМ належать діапазону від 10–38 до 1038
Константи скалярних типів поділяються: на символьні, цілі, плаваючі.
Символьні константи зображуються в три способи:
а) символом алфавіту в апострофах ('А', 'а', '5');
б) конструкцією '\ddd', де ddd – послідовність з 1–3 вісімкових цифр 0, 1, ..., 7;
в) конструкцією вигляду '\символ'.
Таблиця 1
Тип |
Ім'я типу |
Розмір |
Символьні |
char |
1 |
Цілі |
int |
2 чи 4 |
короткі |
short або short int |
2 |
довгі |
long або long int |
4 |
Плаваючі |
float |
4 |
довгі |
double або long tloat |
8 |
Беззнакові цілі |
unsigned або unsigned int |
2 чи 4 |
короткі |
unsigned short |
2 |
довгі |
unsigned long |
4 |
символьні |
unsigned char |
1 |
Часто використовуються конструкції
'\п' — символ нового рядка,
'\r' — символ повернення каретки,
'\t' — символ вертикальної табуляції, ' \Ь' — символ повернення на крок,
'\f' —символ переведення формату,
''\\' — зворотна коса,
'\'' — апостроф,
'\”' — лапки,
'\0' — нуль-символ. Слід відрізняти нуль-символ від символу '0';
Символи вживаються також як цілі. Діапазон цілих, відповідних символам, залежить від реалізації, але символ '\0' завжди має ціле значення 0.
Описи скалярних змінних.
Змінні – це дані, значення яких можуть змінюватися під час виконання програми. Змінну можна розглядати як частину пам’яті ЕОМ: ім’я змінної вживається для звернення до цієї пам'яті, а різні стани пам'яті відповідають різним значенням. Використання та зміна цих значень визначаються типом змінної.
Клас пам'яті, тип та ім'я змінної мають бути в описі (означення класу пам'яті розглядатиметься пізніше). Описи скалярних змінних мають вигляд
ім'я-типу перелік-імен-змінних;
де ім'я-типу є одним з імен типів у табл. 1; імена змінних у переліку відокремлюються комами. Наприклад, описи char a, b; int c, х, у; визначають символьні змінні а, b та цілі змінні с, х, у.
У мові Сі булевий тип відсутній, тому хибність подається цілим значенням 0, істина — будь-яким ненульовим значенням.
Операції та вирази.
Вирази описують процеси породження значень застосуванням операцій над даними. Вирази бувають: арифметичні, присвоювання, відношення, логічні. Тип виразу і породжуваного ним значення визначається за операціями та типами операндів у виразі.
Первинними виразами, які не містять знаків операцій, є імена змінних і константи. Значення константи — це відповідний елемент типу, ті якого вона належить. Значення виразу, що є іменем змінної, — це значення змінної, тобто з появою імені змінної до нього застосовується не позначена явно операція «добути значення».
Таблиця 2.
Групи операцій |
Знаки операцій |
Дужки та адресні |
( ) [ ] . –> |
Унарні |
++ – – (type) ~ ! & * sizeof |
Арифметичні мультиплікативні |
* / % |
Арифметичні адитивні |
+ – |
Зсуви |
<< >> |
Відношення, І |
< <= > >= |
Відношення, ІІ |
= = != |
Побітова кон’юнкція |
& |
Побітове додавання за mod 2 |
^ |
Побітова диз’юнкція |
| |
Логічна кон’юнкція |
&& |
Логічна диз'юнкція |
|| |
Умовна (тернарна) |
? : |
Присвоювання |
= += -= *= /= %= >>= <<= &= |= ^= |
Кома |
, |
Складнішими від первинних є вирази, утворені з операндів, знаків операцій та дужок. Операнди – це константи, змінні, покажчики функцій та вирази. Вирази, в яких всі первинні – константи, називаються константними; значення таких виразів обчислюються під час трансляції, і вони вживаються скрізь, де допустимі константи. Порядок виконання операцій у виразах відповідає їхньому старшинству (пріоритету): за відсутності дужок, що явно задають порядок, старші операції виконуються раніше, ніж молодші. Операції з однаковим пріоритетом у виразах виконуються зліва направо, за винятком операцій унарних, присвоювання та умовної (табл. 2).
4.
Рівняння
дотичної і нормалі
до кривої.
Рівняння прямої, яка проходить через
точку М0
(х0;
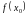 )
з кутовим коефіцієнтом, що дорівнює k,
як
відомо з курсу аналітичної геометрії,
має такий вигляд:
)
з кутовим коефіцієнтом, що дорівнює k,
як
відомо з курсу аналітичної геометрії,
має такий вигляд:
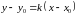 .
.
Дотична до кривої у = f (х) в точці Мо (х0; f (x0)) має кутовий коефіцієнт k, який дорівнює f (x0). Звідси рівняння цієї дотичної запишемо у вигляді:
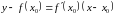 . (6)
. (6)
Пряма,
перпендикулярна до дотичної до кривої
y
= f(x)
у
точці М0(х0;
f(х0))
і яка проходить через точку М0,
називається нормаллю до цієї кривої в
точці М0.
Оскільки кутові коефіцієнти двох взаємно
перпендикулярних прямих у площині
зв'язані співвідношенням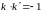 ,
то
рівняння нормалі до кривої у
=
,
то
рівняння нормалі до кривої у
=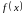 в точці М0(х0;
f
(х0))
запишемо
в такому вигляді:
в точці М0(х0;
f
(х0))
запишемо
в такому вигляді:
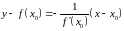 . (7)
. (7)
Основні правила диференціювання функцій
Неперервність
диференційовної функції.
Функція f
(х)
називається
диференційовною в точці х,
якщо
вона в цій точці має скінченну похідну.
Функція f(х)
називається
диференційовною в інтервалі
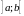 ,
якщо
вона диференційовна в кожній точці
цього інтервалу. Операція знаходження
похідної від даної функції називається
диференціюванням цієї функції.
,
якщо
вона диференційовна в кожній точці
цього інтервалу. Операція знаходження
похідної від даної функції називається
диференціюванням цієї функції.
Лема 1. Якщо функція f (х) диференційовна в точці х, то вона в цій
точці неперервна.
Доведення. Нехай в точці х існує похідна
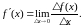
Звідси і з рівності
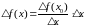
за теоремою про границю добутку маємо:
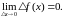
А це означає, що функція f (х) в точці х неперервна.
Похідна суми, добутку і частки.
Теорема
1.
Якщо
функції
і
 диференційовні
в точці х, то
диференційовні
в точці х, то
в цій точці диференційовна функція f (х) + , причому
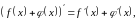 (1)
(1)
тобто похідна суми диференційовних функцій у точці х дорівнює
сумі похідних цих функцій у цій точці х.
Доведення.
Позначивши
через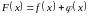 ,
маємо
,
маємо
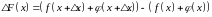 ,
звідси
,
звідси
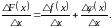 (2)
(2)
Якщо умови теореми виконані, то
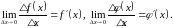 (3)
(3)
З рівності (2) за допомогою теореми про границю суми дістанемо
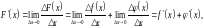
тобто функція диференційовна в точці х і має місце рівність (1).
Теорема
2.
Якщо
функції
і
диференційовні в точці х, то функція
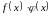 також
диференційовна в цій точці, причому
також
диференційовна в цій точці, причому
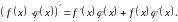 (4)
(4)
Доведення.
Позначивши через
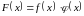 ,
маємо
,
маємо
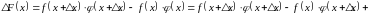
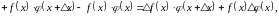 звідси
звідси
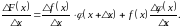 (5)
(5)
Якщо
виконані умови теореми, то правильні
рівності (3),
а
внаслідок леми 1

З рівності (5) за допомогою теорем про границю добутку і суми дістанемо
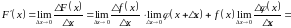
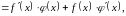
тобто
функція
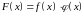 диференційовна в точці х
і правильна
диференційовна в точці х
і правильна
рівність (4).
Якщо
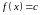 для
для
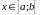 ,
то
,
то
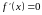 для
,
для
,
тобто похідна від постійної функції дорівнює нулю.
Доведення.
Маємо:
 звідси
звідси
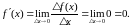
Наслідок
1.
Якцо
функція
f
(x) диференційовна
в точці х,
то
функція cf
(х),
де
с
–
постійне
число, також диференційовна в цій точці
х, причому
 , (6)
, (6)
тобто постійний множник можна виносити за знак похідної.
Наслідок 2. Різниця двох функцій, диференційовних у точці х, є функція, диференційовна в цій точці х, причому
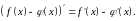
Теорема
3.
Якщо
функції
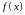 і
і
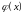 диференційовні
в точці х і якщо
диференційовні
в точці х і якщо
в
цій точці
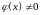 ,
mo функція
,
mo функція
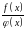 диференційовна в точці х,
диференційовна в точці х,
причому
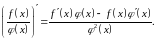 (7)
(7)
Доведення.
Позначивши через
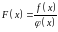 ,
маємо
,
маємо
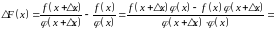


Звідси
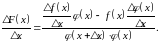 (8)
(8)
Якщо
виконані умови теореми, то правильні
рівності (3),
а
внаслідок леми 1
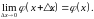
З рівності (8) за допомогою теореми про границю, суми, добутку і частки дістаємо
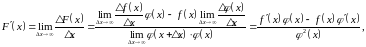
тобто функція диференційовна в точці х і правильна рівність (7).
Наслідок
3.
Якщо
функція
диференційовна
в точці х,
причому
,
то в точці х диференційовна функція
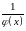 , причому
, причому