R = 2000000/( а 1 5 2 , 2 5 % - а 5 2 , 2 5 % ) =

= 2000000/(12,61216551 - 4,67945253) = 252,11 тыс рб .

4.7 АННУИТЕТЫ С НЕИЗВЕСТНЫМИ СРОКАМИ

Предположим, что человек занимает 10 млн рб и согласен выплатить долг при норме процента j4 = 4% платежами по 500 тыс рб в конце каждого квартала в течение необходимого времени. Ясно, что платежи образуют аннуитет, текущая стоимость которого на день займа равна 10 млн рб. То есть

10000 тыс рб = 500 × а		1% тыс рб	или	а				1% = 20 ,
	п				п

где n является неизвестным. Обратившись к таблицам, мы увидим, что для целого n полученное равенство не может удовлетвориться, действительно,

а				1% = 19,66037934	и	а				1% = 20,45582113 .
	22						23

В этой ситуации обычно делается 22 платежа по 500 тыс рб каждый, а 23-ий платеж делается меньшей суммой, но достаточной, чтобы расплатиться с долгом.

В общем случае,		когда заданы		A , R	и	i ,	практически никогда
соответствующий		параметр	n	не бывает		целым. Поэтому приходится
использовать	один платеж, отличающийся					от	R , чтобы обеспечить
эквивалентность		выплат. Обычно этот платеж является последним и по
величине меньше, чем R , хотя это и не является необходимым.
Определение	величины		последнего		платежа		производится	с

использованием все того же уравнения эквивалентности. Рассмотрим это на примерах.

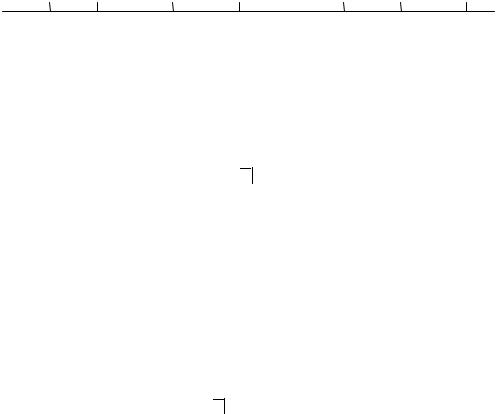
ПРИМЕР 1 Предположим, что заемщик в вышеописанной ситуации подписывает сделку с 22-мя поквартальными платежами и последним платежом в конце 23-го квартала величиной F, достаточной для погашения оставшейся части долга. Чему равна F ?

РЕШЕНИЕ Представим исходные данные на временной диаграмме

56

0	1	2	3	...	21	22	23
	500т	500т	500т	...	500т	500т	F

10 млн

Способ 1. Выпишем уравнение эквивалентности, используя в качестве даты сравнения конец 22-го периода. Это даст

F (1,01) -1 + 500 s22 1% = 10000 × (1,01) 22 .

Разрешая это уравнение относительно F , получим

F = ( 12447,16 - 12235,79 )(1,01) = 231,5 тыс рб.

Способ 2. Введем по одному дополнительному платежу 500 тыс рб в день окончания 23-го периода и используем эту дату как дату сравнения в уравнении эквивалентности получившихся платежей

F + 500 s23 1% = 10000 × (1,01) 23 + 500

F = 12571,63 + 500 - 12858,15 = 213,5 тыс рб.

Когда заданы величины S , R и i , расчет серии платежей проводится аналогично.

ПРИМЕР 2 Вклады по 10000 рб делаются в сберегательный банк по полугодиям при норме процента j2 = 3% . На какую дату попадает заключительный вклад, не превышающий 10000 рб, если сумма на депозитном счете становится равной 300000 рб ? Каким будет этот заключительный вклад ?

РЕШЕНИЕ Вклады будут образовывать аннуитет с итоговой суммой 300000 рб. Поэтому имеет место равенство

300000 = 10000 × s			или	s				1,5% = 30 ,
		1,5%
	п				п

где n неизвестно. Из таблиц находим, что

s				1,5% = 28,63352080	и	s				1,5% = 30,06302361 .
	24						25

57

Следовательно,		нужно	сделать	24 вклада		по	10000 рб и
заключительный вклад			F в конце 25-го периода. Представим это на
временной диаграмме
0	1	2	3 ...	23	24	25
	10т	10т	10т ...	10т	10т	F
						300т
F определяется из подходящего уравнения эквивалентности.
Способ 1.	В качестве		даты сравнения		используем		конец двадцать
четвертого интервала платежа; тогда имеем

F (1,015) -1 + 10000 s24 1,5% = 300000 (1,015) -1

Разрешаем это равенство относительно F

F = 300000 - 290630 = 9370 рб.

Способ 2. Добавим по вкладу 10000 рб в каждую строчку диаграммы в конце двадцать пятого периода и выберем эту дату в качестве даты сравнения уравнения эквивалентности.

F + 10000 s25 1,5% = 300000 + 10000 ,

откуда получаем

F = 310000 - 10000 × 30,06302361 = 9370 рб.

4.8ОПРЕДЕЛЕНИЕ ЗАКЛЮЧИТЕЛЬНОГО ПЛАТЕЖА

СПОМОЩЬЮ ИНТЕРПОЛЯЦИИ

Когда	A , R и i ( или S , R и i ) заданы, уравнение аннуитета A = R а						i
					п
( или	S = R s			i ) может быть разрешено относительно n или путем
		п

интерполяции или при помощи логарифмирования. Процедура расчета простая, но появляется проблема интерпретации нецелого решения.

Например, если уравнение аннуитета приводит к равенству а п i = 20 ,

58

как	встретилось	в предыдущем разделе, интерполяция дает результат
n =	22,42696.	Легко проверить, что произведение дробной части этого

решения на величину периодического платежа дает точное значение заключительного платежа F , определяемого в примере 1 ,

500000 × 0,42696 = 21348 рб.

Оказывается это имеет место и в общем случае.

Пусть даны A , R и i . Значение n

определим с помощью интерполяции.

Представим

n

в виде

k + f

, где

k

- целое число, а f - дробная часть,

f < 1. Тогда

F

=

f R

равно заключительному платежу, выплачиваемому

через один период после последнего

платежа

R и обеспечивающему

эквивалентность

платежей.

Докажем

это.

Из

уравнения аннуитета

имеем а

i

= A/R . Составим таблицу данных

п

k

k + f

k + 1

a

i

A / R

a

i

k

k 1

Из уравнения пропорции получим

f

A

R

a

i

k

1

a

i

a

i

k

1

k

Знаменатель этой формулы можно вычислить по формуле (10) при n = 1 с учетом того, что a 1 i = (1 + i) -1 . Это дает следующее выражение для f

	A	R	a				i
f					k
	1		i	k 1

Умножая это равенство на R(1 + i) -k-1, получим

f R (1 + i) -k-1 = A - R a k i .

С другой стороны, если F определять при помощи уравнения эквивалентности с датой сравнения в начале первого интервала платежа, мы получим согласно диаграмме

59

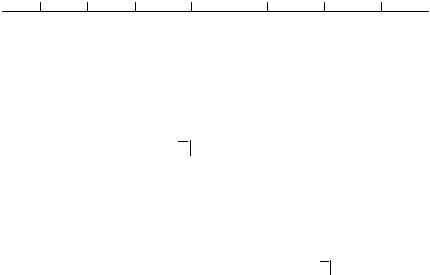
0	1	2	3 ... k-1	k	k+1
A	R	R	R ... R	R	F

следующее уравнение эквивалентности стоимостей

A = R a k i + F(1 + i) -k-1 .

Сравнивая этот результат с предыдущим, убеждаемся, что в условиях линейной интерполяции F = f R , что и требовалось.

Таким образом, когда уравнение аннуитета a п i = A/R разрешается

относительно n приближенно при помощи линейной интерполяции, дробная часть n может интерпретироваться как дробная часть R , необходимая в качестве заключительного платежа F , когда F выплачивается одним периодом позже последнего платежа R .

В заключение заметим, что точное значение n находится из уравнения аннуитета, записанного в явной форме

a				1 1 i n			A
			i
				i			R
	n
что может быть переписано более удобно
			(1 -iA/R)(1 + i) п		= 1 .
Логарифмируя это равенство и выражая затем							n , получим его точное
значение в виде

n = - (log(1 - iA/R)) / log(1 + i) .

К сожалению, это выражение не поддается практической интерпретации.

60