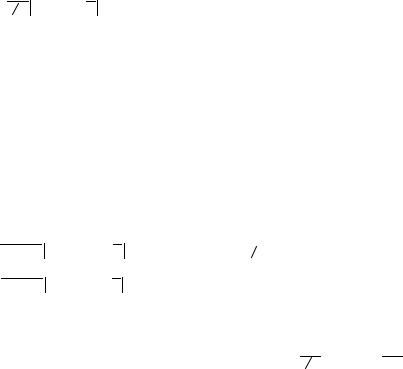
F = R ( s 1 2 3 % - s k 3 % )(1,03) -1/3 = 0,0551 млн рб .

Способ 2 (интерполяция). Как и в предшествующем решении, мы

сначала определим, сколько нужно платежей.

Так как понадобится 21

полных

платежей

и

22-ой

частичный

платеж,

интерполяция

производится между значениями, соответствующими

q = 21 и

q = 22.

Поэтому

мы

определим

n , а

отсюда

и q

,

интерполяцией

между

значениями

а

и

а

3 % .

Однако,

нет

необходимости

3 1 / 2

3 %

4 1 / 3

вычислять эти функции, так как из известных тождеств видно

а

а

3 1 / 2 3 % = а 4 3 % - (1,03) 4 1 / 3 3 % = а 4 3 % - (1,03)

	-4	s
			1 2		3 %
	-4	s
			1 / 3		3 %

,

,

что интерполяция между членами левой

части для

n

эквивалентна

интерполяции для

s

k

между

значениями

s 1

2

3 % и s 1 / 3

3 % .

Используя значение

= 0,477985 как найденное в предыдущем

k

3 %

решении, мы образуем следующую интерполяционную табличку

q

21

21 + f

22

s

k

1/2

1/3

0,496305 0,477985

0,330054

k

3 %

Интерполируя, мы получим f = 0,018320/0,166251 =

0,11019 и F = f W =

= 0,0551.

Хотя каждое из решений последнего примера представляется длинным, будет видно, что они являются наглядными и требуют немного вычислительной работы. Более того, все функции, встречающиеся в вычислениях, обычно табулированы с точностью до восьми десятичных знаков, посредством чего обеспечивается точность окончательного результата по крайней мере до семи значащих цифр.

10.4 ДОКАЗАТЕЛЬСТВО ОБЩЕЙ ТЕОРЕМЫ ИНТЕРПОЛЯЦИИ

165

Пусть

A

будет текущей стоимостью

аннуитета,

W

- периодический

платеж,

p

- число платежей за

год,

i

-

норма процента за период

конверсии

и

m

-

число

периодов

конверсии

в

год.

Когда

вышеперечисленные величины

заданы, аннуитет

обычно

является

нестандартным,

так

что заключительный платеж

F ,

рассчитываемый

на дату через один интервал платежа после

последнего платежа

W ,

для эквивалентности необходимо определять.

Если

q ,

число платежей,

определяется

путем

интерполяции

между

значениями,

соответствующими

последовательным

целочисленным

значениям

q ,

тогда дробная

часть

f

этого

решения,

умноженная на

W

,

дает

заключительный платеж.

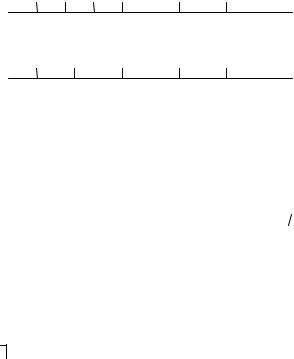
Доказательство Предположим сначала, что аннуитет является обыкновенным аннуитетом, так что временные диаграммы платежей выглядят следующим образом

Интервалы платежа :

0 1

2

3 ...

q

q + 1

W W W ... W

F

A

Периоды начисления :

0

1

2 ...

n'

n"

где n' = q (m/p) и n" = (q

+

1)(m/p)

. Уравнение эквивалентности с

исходной датой в качестве даты сравнения имеет вид

A = R a

i + F (1 + i) -n",

где R = W / s

i .

n'

m p

Поэтому

F = (A - R a

i )(1 + i) n"

(a)

n'

Если мы установим an i = A / R , тогда n = (q + f)(m/p) , где f лежит между

0 и 1. Интерполирование по n

между

n' и n"

эквивалентно

интерполированию по f , что дает

f = (A/R - a

i ) / ( a

i - a

i ) .

n"

n'

n'

Отсюда

A - R a

i = f R ( a

i - a

i ) .

(b)

n'

n"

n'

166

Исключая A из (a) и (b) , получим

F = f R ( an" i - an' i )(1 + i) n" .

Используя тождество (10) из параграфа 4.4

an" i - an' i = an" п' i (1 +i ) n"–n' ,

приходим к равенству

F = f R an" п' i (1 +i ) n"–n' = f R sn" п' i .

Но n" - n' = m/p и R sт p i = W , поэтому F = f W .

Если аннуитет является полагающимся аннуитетом, включая F , приходится на один период раньше преобразуется к виду

(c)

каждый платеж, и равенство (a)

F = (A - R an' i )(1 + i) n' , где R = W / ат p i .

Равенство (c) принимает вид

F = f R an" п' i = f R ат p i = f W .

10.5	ДРУГИЕ ВИДЫ АННУИТЕТОВ
Имеется несколько других видов аннуитетов,			которые	иногда
встречаются. Некоторые из них кратко рассмотрены ниже.
Увеличивающиеся аннуитеты		Этот термин	применяется		к
последовательности периодических платежей W ,			2W , 3W , ... , qW ,
каждый из которых на	W больше	предыдущего пока не будет сделано

q платежей. Как обычно, пусть i обозначает норму процента за период

конверсии, m -		число периодов конверсии в год, p -			число платежей в
год	и n = qm/p		число	периодов начисления	в течение срока
аннуитета. Для того, чтобы				найти итоговую сумму такого аннуитета,
мы	рассмотрим	его	как	совокупность q следующих отдельных

167

аннуитетов : один аннуитет с					q платежами по			W , другой аннуитет с
q - 1	платежами	по	W , третий аннуитет с				q - 2	платежами по W и
т.д.,	все эти аннуитеты заканчиваются в одно и то же время, как показано
на временной диаграмме
	0	1	2	3	4 ...	q - 2 q - 1			q
		W	W	W	W ...	W	W		W
			W	W	W ...	W	W		W
				W	W ...	W	W		W
						............................
							W		W
									W

Каждый из аннуитетов будет эквивалентен простому аннуитету с

платежами по

R = W / s

i

и со сроками

qm/p ( = n ), (q - 1)m/p ,

т p

(q - 2)m/p ,

... , 2m/p и, наконец,

m/p

. Поэтому итоговая сумма

увеличивающегося аннуитета равна

S = R s

i

+ R s

i

+ R s

i

+ ... + R s

i

.

п

q 1 т p

q 2 т p

т p

Если функции составных платежей представить в явной форме и выполнить упрощающие преобразования, тогда получим

S = R ((1+ i) п + (1+ i) (q–1)m/p + ... + (1+ i) m/p - q)/i

Сумма в скобках этого выражения является геометрической прогрессией с q членами, первый член равен (1+i) п , и знаменателем (1+i) п . Используя формулу для суммы геометрической прогрессии, мы получим

S = R (((1+i) п - 1)/(1 - (1+i) -m/p) - q) / i = R (( s			i / а				i ) - q) / i	(7)
	п			т p

последнее упрощение использует деление числителя и знаменателя предшествующей дроби на i .

Если требуется найти настоящую стоимость или другую эквивалентную стоимость увеличивающегося аннуитета, рекомендуется сначала определить его итоговую сумму из равенства (7), а затем преобразовывать ее к желаемой дате.

168

Уменьшаюшиеся аннуитеты Уменьшающийся аннуитет отличается от

увеличивающегося аннуитета только тем, что первый платеж равен

qW

и каждый

последующий

платеж на

W меньше предыдущего до

тех

пор

пока

не

достигнут заключительный платеж W . Так как

этот

аннуитет

может рассматриваться как сумма q

различных аннуитетов,

начинающихся в

одно

и

то же время, проще

определять формулу для

его настоящей стоимости,

а не для итоговой суммы. Формула имеет вид

A = R (q - ( а

i / s

i )) / i ,

(8)

п

m p

где

R = W / s

i . Ее

доказательство

подобно доказательству формулы

m p

для увеличивающегося аннуитета и предлагается сделать читателю в качестве упражнения. Если уменьшающийся аннуитет должен быть рассмотрен для даты, отличающейся от начальной, рекомендуется сначала вычислить его настоящую стоимость, а затем преобразовать ее к требуемой дате.

Наконец, следует заметить, что если аннуитет является увеличивающимся или уменьшающимся полагающимся аннуитетом, R , встречающееся в равенствах (7) или (8) следует вычислять с помощью

равенства (1) главы 10, R = W/ а			i .
		m p
Аннуитеты,	выплачиваемые непрерывно			Этот	тип аннуитетов
относится к сбору конечных сумм денег T , в каждый период начисления,
когда деньги собираются непрерывным потоком				в течение периода. Хотя
непрерывные	аннуитеты в реальном бизнесе не				встречаются, они

достаточно близко приближаются в определенных практических случаях, таких как поток монет в системе городского метро.

Для получения формул для текущей стоимости и итоговой суммы такого аннуитета необходимы два соотношения из анализа

p ((1+i) m/p - 1) m ln (1+i) ,			когда				p	(9)
(1 + 1/x) х e = 2,71828... ,			когда				x	(10)
Настоящая стоимость обыкновенного общего							аннуитета	может быть
записана в виде
A = W а		i / s				i .		(11)
	п		m p

169

Пусть T = p W будет равно полным платежам аннуитета за год. Тогда

A = T i ап i / (p ((1+i) m/p - 1)) .

Если мы устремим p к бесконечности и используем предел из соотношения (9), мы получим

A T i а			i / (m ln (1+i))			,	когда	p		(12)
	п
Подобным образом
S T i s					i / (m ln (1+i))	,	когда	p .		(13)
			п
Аннуитеты с процентами, начисляемыми непрерывно									Возвращаясь		к
равенству (11), будем считать p постоянным,								i =	j/m ,	n = tm	,

где t равно продолжительности полного года. Тогда

1

1

j tm

i

A W

m

.

j m p

j

1

1

m

m

Это последнее соотношение может быть записано в виде

	1				1	j		m / j jt
A W							m			.
			1		j m / j			j / p	1
					m

Если теперь m устремить к бесконечности, соотношение (10) при x = m/j дает

A W (1 - e –jt ) / (e j/p- 1) , S W (e jt – 1) / (e j/p- 1) .

Вышеприведенные формулы применяются к аннуитетам, для которых платежи делаются конечное число раз в год, но процент конвертируется непрерывно.

170