Глава 5 ОБЫКНОВЕННЫЕ ОБЩИЕ АННУИТЕТЫ

5.1 ВВЕДЕНИЕ

Как мы видели, основные задачи финансовой математики связаны с расчетами эквивалентности различных серий финансовых обязательств в связи с тем, что денежные суммы в различное время стоят по-разному. сегодняшние 100 рб эквивалентны 105 рб через год при норме процента 5% годовых. Подобно этому дом, который стоит 120 млн рб при оплате наличными, может быть куплен за 20 млн рб наличными и ежеквартальными платежами по 2154,8 тыс рб в течение 20 лет при норме процента 6% , конвертируемых поквартально. Основным средством решения таких задач финансовой математики является уравнение эквивалентности. Для численного решения задач разработаны формулы и составлены таблицы, позволяющие быстро получать решения в стандартных ситуациях. Когда встречаются нестандартные ситуации рекомендуется пытаться расчленить исходную задачу на стандартные, для решения которых уже можно пользоваться имеющимися таблицами или формулами. Это позволяет составлять достаточно компактные таблицы, позволяющие при отсутствии средств вычислительной техники довольно быстро решать разнообразные задачи. Конечно, когда средства вычислительной техники являются доступными, численное решение таких задач не является сложной проблемой.

Аннуитет был определен как последовательность платежей, обычно равной величины, делаемых через равные промежутки времени. Он был назван простым аннуитетом, если интервал платежа точно совпадает с периодом конверсии; в противном случае он называется общим аннуитетом. Например, предположим, что Иванов вносит вклады по 50 тыс рб на счет в сберегательном банке в конце каждого квартала. Если банк начисляет проценты поквартально, вклады образуют простой аннуитет. Если банк использует другой период конверсии, вклады образуют общий аннуитет.

Внимательный читатель заметит, что общий аннуитет мог бы быть исследован путем замены данной нормы процента на эквивалентную, составляемую с желаемой частотой. Это так, но новая рента может оказаться такой, для которой не составлены таблицы аннуитетов, что не позволит удобным образом решить задачу для заданного аннуитета. Поэтому возникает задача замены данного общего аннуитета такими

65

эквивалентными обыкновенными простыми аннуитетами, для которых можно было бы эффективно воспользоваться имеющимися таблицами или формулами. Еще раз подчеркнем, что будем рассматривать только общие аннуитеты с платежами в конце интервалов платежа.

5.2ПРЕОБРАЗОВАНИЕ ОБЫКНОВЕННЫХ ОБЩИХ АННУИТЕТОВ

ВПРОСТЫЕ АННУИТЕТЫ

Введем обозначения :

W - платежи общего аннуитета;

p - количество платежей общего аннуитета в год; i - норма процента за период конверсии;

m - число периодов начисления процента в год;

R - платежи обыкновенного простого аннуитета, который является эквивалентной заменой общего аннуитета, делаемые m раз в год.

Если аннуитет заменяется другим аннуитетом, то очевидно должны быть выполнены следующие два условия : a) норма процента должна быть той же самой или эквивалентной; b) стоимости обоих аннуитетов должны быть одинаковыми в любой момент времени.

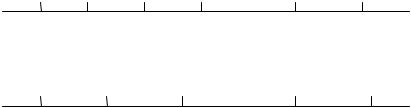
Обыкновенный общий аннуитет с платежами W , делаемыми p раз в год, и нормой процента i за период конверсии с m периодами конверсии в год

и обыкновенный простой аннуитет с платежами					R ,	делаемыми m раз
в год удобно представить на временных диаграммах :
0	1/p	2/p		3/p ... (p-1)/p		1
	W	W		W ...	W	W
0	1/m		2/m ... (m-1)/m			1
	R		R	...	R	R

Для того, чтобы эти аннуитеты были эквивалентными, определим норму процента i' за интервал платежа общего аннуитета, которая эквивалентна норме i за период начисления процента. Тогда ( см. раздел 2.6 )

(1 + i') р = (1 + i) т .

(1)

66

Если теперь приравнять аннуитеты в конце года, получим

R s

i = W s

i .

(2)

m

p

Заменяя функции составных платежей

s

i и

s

i их явными

m

p

выражениями в обеих частях (2), будем иметь

R

1 i m 1

W

1 i p 1

.

(3)

i

i

С помощью (1) это равенство упрощается к виду

R/i = W/i' .

(4)

Разрешая (1) относительно i' находим, что

i' = (1 + i) т/р - 1 ,

Подставляя это в (4) окончательно получаем

R W

i

.

(5)

1 i

m p

1

Дробь в правой части

этого

равенства

является

обратным значением

функции

s

i для дробного параметра n = m/p .

п

Так что справедливы равенства

R W

1

и

W Rs

i .

(6)

m p

sm p

i

Понятно, что значение дроби m/p

в общем случае может быть любым.

Однако практически

встречается

один из следующих вариантов :

a) m/p является целым числом : в этом

случае

для

анализа

общего

аннуитета

можно использовать обычные таблицы

для

целочисленных

значений параметра; b)

m/p

является дробью вида

k/12 , k =

1, 2, 3, 4

или 6 , поскольку такие дроби встречаются довольно часто для них также составлены соответствующие таблицы функций составных платежей.

67

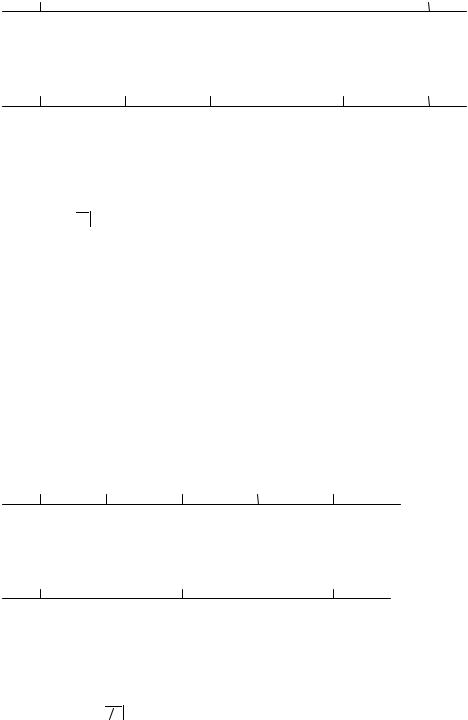
ПРИМЕР 1 Сидоров получает пенсию 5 млн рб в конце каждого года. Какие ежемесячные выплаты эквивалентны этой сумме, если деньги стоят j12 = 6% ?

РЕШЕНИЕ Здесь	W = 5 млн рб,		p = 1,	i = 1/2 % , m = 12 и нужно
определить R .
0		(1 год)			1
					5 млн
0	1	2	...	11	12
	R	R	...	R	R

Использование равенства (6) дает

R = 5000 / s1 2 0 ,5 % = 405,35 тыс рб .

Таким образом, Сидоров мог бы получать ежемесячно 405350 рб вместо получения 5 млн рб в конце года. Такой результат получился бы, если бы мы воспользовались уравнением эквивалентности с датой сравнения в конце года.

ПРИМЕР 2	Заменить платежи по 500 тыс рб в конце каждого квартала
на полугодовые платежи, если норма процента 5% , m = 2 .
РЕШЕНИЕ Мы имеем W = 500000 , p = 4 , i = 2,5 % и m = 2.
0	1	2	3	4
	500т	500т	500т	500т
0		1		2
		R		R

Из уравнения (6) получаем

R = 500/ s1 2 2 ,5 % = 500 × 2,01242284 = 1006,2 тыс рб .

68