8.10 Сравнение двух выборочных средних

Проверять нулевую гипотезу относительно средних ₁ и ₂ двух выборок можно, только если соответствующие оценки дисперсий S₁²и S₂² однородны. Поэтому проверке нулевой гипотезы относительно средних должна предшествовать проверка однородности оценок дисперсий этих выборок.

Проверка нулевой гипотезы относительно двух выборочных средних ₁ и ₂ производится следующим образом.

После проверки однородности оценок дисперсий S₁² и S₂² находят:

(8.28)

и суммарное число степеней свободы

f = f₁ + f₂ , (8.29)

где f₁ и f₂ - число степеней свободы первой и второй выборок соответственно.

Далее рассчитывают значение величины t_расч:

(8.30)

По табл. п 2 Приложения для данного числа степеней свободы f и уровня значимости q находят значение t_табл. Величина t_табл показывает, какое наибольшее значение может принять величина t_расч при условии, что нулевая гипотеза о равенстве двух выборочных средних справедлива. Следовательно, если t_pасч<t_табл, принимают гипотезу о том, что ₁ и ₂ являются оценками одного и того же генерального среднего (математического ожидания) М_у, то есть расхождение между ₁ и ₂ несущественно (незначимо).

Изложенная процедура проверки нулевой гипотезы о двух выборочных средних называется проверкой по t - критерию Стьюдента.

8.11 Проверка гипотезы о виде закона распределения

Функция, показывающая вероятность того, что случайная величина у будет меньше некоторого значения Y, называется функцией распределения случайной величины и обозначается F(y). Производная от функции F(y) называется плотностью распределения f(y), или плотностью вероятности случайной величины у. Плотность вероятности f(y) показывает вероятность попадания случайной величины у на участок от у до (у + Δу) при условии, что приращение Δу стремится к нулю.

Особое место в научных исследованиях занимает нормальное распределение. Для нормального распределения плотность вероятности вы­ражается формулой

(8.31)

где е - основание натурального логарифма.

График нормального распределения показан на рис.8.1.

Рис.8.1 График нормально распределения

Нормальному закону подчиняются случайные у величины, которые являются результатом суммарного взаимодействия многих независимых случайных величин при условии, что степень их воздействия примерно одинакова. Например, нормальный закон описывает распределения длины напорных пожарных рукавов при условии, что отклонение от номинальной длины носит случайный характер.

Вероятность р того, что случайная величина примет значение, лежащее в пределах от у₁ до у₂, равна

(8.32)

Эта вероятность соответствует доле заштрихованной площади от площади под кривой (см. рис.8.1). Если f(y) - плотность распределения длины напорных пожарных рукавов, то вероятность р равна отношению количества напорных пожарных рукавов, длина которых лежит в пределах от у₁ до у₂, к общему количеству обследуемых напорных пожарных рукавов(при условии, что это количество достаточно велико).

Функция распределения случайной величины, полученная из опыта, называется эмпирической функцией распределения. Роль вероятности в этом случае выполняет относительная частота γ_i. Относительная частота γ_i равна отношению количества m_i наблюдений, попавших в данный i-й интервал, к общему количеству наблюдений. Большинство статистических оценок предполагает нормальное рас­пределение результатов опыта и может быть несправедливо в случае дру­гого распределения. Поэтому применение этих оценок допустимо лишь при достаточной уверенности, что распределение наблюдаемых величин близко к нормальному. Для проверки гипотезы о виде распределения используют критерии согласия.

Сущность проверки по критерию согласия состоит в том, что выборка сравнивается с некоторым заранее намеченным теоретическим распределением. Вид теоретического распределения выбирается исходя из соображений, связанных с физикой наблюдаемых явлений или по характеру кривой эмпирического распределения.

В большинстве случаев задаются нормальным теоретическим рас­пределением. Параметры этого распределения – среднееи оценка дисперсииS² - находятся из выборки.

При проверке гипотезы о виде закона распределения используют критерий согласия Колмогорова λ или критерий χ² (хи-квадрат) Пирсона.

Рассмотрим критерий χ² Пирсона. С его помощью можно сравнивать эмпирическое и теоретическое распределения или два эмпирических распределения.

Для проверки гипотезы о нормальности эмпирического распределения по критерию χ² находят сумму отношений квадратов разностей между частотами эмпирического и теоретического распределения к теоретическим частотам:

(8.33)

Где l- количество интервалов, на которые разбиты опытные данные;

р_i - теоретические вероятности попадания данных в i-й интервал,

р_in- теоретические частоты попадания опытных данных в i-й интервал

(с округлением до ближайшего целого числа);

m_i - эмпирические частоты попадания случайной величины в i-й интервал.

Вычисление теоретической вероятности p_i производится по формулам:

(8.34)

(8.35)

где у_iн и y_iв- значения случайной величины, соответствующие нижней и верхней границам i-го интервала;

_о(z) - функция распределения для нормального закона (см. табл. 6 Приложения).

Следует иметь в виду, что для отрицательных значений z справедливо следующее соотношение:

_o(-z) = 1 - _o(z). (8.36)

Результаты вычислений по критерию χ ² можно свести в табл. 8.4.

{тI -Pi«f

pi"

(Шг-р^У

Pfl

Таблица 8.4

Номер интервала	Нижняя граница интервала уiн	Верхняя граница интервала yiв	Эмперическая частота , mi	Z1	Z2	Фo(z1)	Фo(z2)	Р1	рin	(mi - рin)^2
1	2	3	4	5	6	7	8	9	10	11	12
1 2

Просуммировав показания последнего столбца таблицы, получаем значение критерия χ²_расч. Далее определяем число степеней свободы к = i - 3 и задаёмся уровнем значимости q. По табл. п. 5 Приложения находим значение χ²_qf. Если χ²_расч≤ χ²_qf. то гипотеза о нормальности распределения принимается. Эмпирические и теоретические распределения для наглядности могут быть построены на одном графике.

Эмпирические частоты т_i и теоретические частоты р_iп откладываются по оси ординат, причем их относят к средним значениям i-го интервала. Соединив точки, соответствующие теоретическим частотам, получим кривую нормального распределения. Подобный график дает возможность визуально судить о степени близости эмпирического распределения к нормальному.

Рассмотрим пример. В результате измерения времени развертывания насосно-рукавных систем для транспортирования и подачи огнетушащих веществ личным составом дежурных караулов гарнизона пожарной охраны было получено 140 значений времени (табл.8.5). Требуется проверить гипотезу о нормальности распределения времени развертывания насосно-рукавных систем для транспортировки и подачи огнетушащих веществ.

Во 2-й и 3-й столбцы табл.8.6 запишем соответственно нижние и верхние границы интервалов. В следующий столбец вписываем эмпирическую частоту равную количеству наблюдений, попавших в данный интервал. Например, для 1-го интервала (i = 1) находим все наблюдения меньше 450 (см. табл.8.5). Их четыре: 430, 428, 428, 412. Следовательно, m_i= 4. Для второго интервала (i = 2) находим все наблюдения меньше 500 и больше 450. Их восемь, то есть m_i = 8 и т. д. Найдем значения 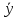иS²:

(8.37)

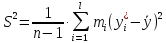(8.38)

Где y_i* - срединное значение каждого интервала. После подстановки получаем:

= 746, S²= 42849.

Следовательно, S = = 207.

Для каждого интервала найдем величины:

(8,39)

Например, для второго интервала zимеем:

;

Значения z₁ и z₂ заносим в пятый и шестой столбцы таблицы. По табл.8.6 Приложения для каждого интервала находим _o(z₁ ) и _o(z₂). Так, для второго интервала

₀(z₂) = ₀(-1,19) = 1 - ₀(1,19) = 0,11702 ;

₀(z₁)= ₀(-1,43) = 1 – ₀(1,43) = 0,07636.

Значения _o(z₁) и _o(z₂) составляют 7-й и 8-й столбцы табл.8.6. Находим pi=_o(z₁) - _o(z₂) = 0,11702 - 0,07636 = 0,4066 и заносим результат в 9-й столбец. В 10-й столбец записываем значения р_iп; в 11-й - результаты вычисления величины (m_i - р_in)²; в 12-й - предыдущее значение, деленное на р_iп. Например, для второго интервала имеем 5,33 / 5,69 = 0,937. Суммируя показания последнего столбца, получаем значение χ² = 14,143.

Определим число степеней свободы k =i - 3 = 18 – 3 = 15 и зададимся уровнем значимости q= 5%. По табл. п.5 Приложения находим значение χ ²_табл = 28. Так как χ²_расч<χ ²_табл, то гипотеза о нормальности распределения принимается.

Таблица 8.5