11.8 Анализ результатов эксперимента

Это заключительный этап планирования эксперимента, на котором исследователь, пользуясь построенной моделью, получает необходимую информацию об объекте исследования. Анализ модели лучше всего проводить, пользуясь уравнением регрессии в нормализованных обозначениях факторов.

Важную информацию несут знаки коэффициентов регрессии. Например, если линейный коэффициент регрессии положителен, то выходная величина возрастает с увеличением соответствующего фактора и убывает при его уменьшении.

По уравнению регрессии можно оценить относительную степень влияния варьируемых факторов на изменение выходной величины (отно­сительную важность факторов). Для этого используют значения t - критерия, вычисленные для каждого линейного коэффициента регрессии по формуле (11.26). Чем больше величина t_pacч, тем сильнее влияние соответствующего фактора на изменение выходной величины.

Для ПФП оценки дисперсий всех коэффициентов регрессии равны друг другу (см. (11.25)). Это позволяет оценивать относительную значимость факторов для этих планов непосредственно по абсолютным величинам линейных коэффициентов регрессии.

Уравнение регрессии позволяет предсказать значение у для любой точки внутри области варьирования факторов. С его помощью можно строить графики зависимости у от любого фактора при фиксированных значениях остальных факторов.

Наконец, построенная математическая модель может послужить основой для оптимизации исследуемого процесса и для управления им.

Для получения модели в натуральных значениях факторов следует заменить нормализованные факторы в уравнении регрессии натуральными по формуле (11.4).

12. Исследование оперативно-тактических действий с применением дробных факторных планов.

Дробные факторные планы (ДФП), как и полные факторные планы (ПФП), предназначены для построения математической модели объекта. При заданном числе факторов ДФП содержат меньшее число опытов по сравнению с ПФП. Но эта экономия достигается ценой упрощения математической модели.

Напомним, что по результатам ПФП 2^k можно оценить свободный член в математической модели, все линейные коэффициенты регрессии и все взаимодействия факторов. Однако во многих случаях учёт всех взаимодействий факторов не вызывается необходимостью. Так, при первоначальном изучении объектов широко применяются эксперименты с целью получения линейной модели. Для k варьируемых факторов такая модель имеет следующий вид: (12.1) и содержит (k + 1) коэффициент регрессии

(12.1)

Эксперимент, позволяющий отыскать эти коэффициенты, должен содержать не менее чем (k + 1) опытов. С точки зрения экономии средств, желательно, чтобы число опытов N не слишком превышало эту величину. С этой позиции ПФП при отыскании линейной модели неудовлетворительны. В силу соотношения N = 2^k число опытов ПФП существенно превосходит величину (k + 1), начиная уже с трёх факторов. Полные факторные планы неэкономичны, даже если экспериментатора интересуют помимо линейных коэффициентов регрессии некоторые (но не все) взаимодействия факторов.

Пусть, например, по результатам эксперимента с шестью факторами (k = 6) необходимо оценить свободный член, линейные коэффициенты регрессии и парные взаимодействия. Минимально необходимое для этого число опытов равно числу коэффициентов регрессии:

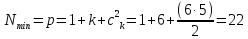(12.2)

в то время как ПФП 2^k шести факторов содержит N = 2⁶ = 64 опыта.

Дробные факторные планы позволяют сократить число опытов по сравнению с ПФП в случае, если в уравнении регрессии можно заранее пренебречь некоторыми взаимодействиями факторов. Для уяснения идеи построения дробных факторных планов обратимся сначала к плану ПФП 2² с двумя факторами (табл. 12.1).

Таблица 12.1

Матрица базисных функций ПФП 2² для модели (12.2)

Номер опыта	хо	ПФП 2.2		x3 (x1x2)	y
		x1	x2
1	2	3	4	5	6
1	+ 1	-1	-1	+1	y1
2	+ 1	+ 1	-1	-1	y2
3	+1	-1	+ 1	-1	y3
4	+1	+1	+1	+1	y4

Собственно экспериментальным планом являются только столбцы 3 и 4 табл. 12.1. Столбец х₀ добавлен для вычисления коэффициента регрессии b₀, а столбец x₁х₂ - для вычисления коэффициента b₁₂ при произведении факторов x₁ и х₂. Следует отметить, что полученная матрица базисных функций удовлетворяет трём свойствам - (11.5) - (11.7). По результатам такого эксперимента можно получить модель в виде

(12.3)

Предположим теперь, что имеется объект с тремя варьируемыми факторами x₁, х₂, х₃, причём целью эксперимента является построение линейной модели, то есть имеются основания пренебречь всеми взаимодействиями факторов. В таком случае можно опять воспользоваться матрицей плана 2² в табл. 12.1. Потребуем, чтобы в этом эксперименте факторы x₁ и х₂ по-прежнему варьировались в соответствии с элементами столбцов 3 и 4, а фактор х₃ варьировался так же как и взаимодействие факторов x₁ х₂ (столбец 5 табл. 12.1.).

Таким образом, для эксперимента с тремя факторами получен план из четырёх опытов, по результатам которого можно построить линейную модель:

(12.4)

Перепишем матрицу этого плана в табл. 12.2

Таблица 12.2

Номер опыта	x1	x2	x3	y
1	-1	-1	+1	y1
2	+1	-1	-1	y2
3	-1	+1	-1	y3
4	+1	+1	+1	y4

Планы такого типа называются дробными факторными планами (ДФП) или дробными репликами полных факторных планов. В частности, план, приведённый в табл. 12.2, называется полурепликой (или 1/2 реплики) от ПФП 2². Его обозначение 2^3-1 . Здесь 3 - число факторов, а единица вверху символизирует тот факт, что только одно взаимодействие заменяется новым фактором. Именно такие ДФП и называются полурепликами.

В ДФП 2^3-1фактор х₃ варьируется одинаково с парным взаимодействием x₁ х₂. Поэтому в уравнении регрессии нельзя отделить влияние фактора х₃ от влияния взаимодействия x₁ х₂. Если обозначить через β истинные величины соответствующих коэффициентов регрессии, то можно сказать, что коэффициент β₃ даёт совместную оценку двух истинных коэффициентов регрессии β ₃ и β₁₂ : b₃ → β ₃ + β₁₂ - это так называемая смешанная оценка.

Если построить столбцы х₁ х₃ и х₂ х₃, то легко убедиться, что они совпадут со столбцами х₂ и х₁ соответственно (рекомендуется проделать это самостоятельно). Следовательно, имеем дополнительно смешанные оценки:

(12.5)

(12.6)

При построении данной полуреплики 2^{3- 1} было использовано соотношение х₃ = х₁ х₂, которое называется генератором плана. Умножим обе его части на х₃: х₃₂= х₁ х₂ х₃. Но = 1, так как нормализованный фактор х₃ в эксперименте равен либо +1, либо -1; следовательно, имеем 1 = х₁х₂ х₃.

Такое соотношение, в левой части которого стоит 1, а в правой - некоторое произведение факторов, называется определяющим контрастом (ОК) данной реплики. С помощью ОК легко определить систему смешивания оценок, не прибегая к построению дополнительных столбцов. Для этого обе части ОК умножаются поочерёдно на х₁ х₂ х₃. Получим х₁= х₂ х₃. Откуда следует:

(12.7)

(12.8)

откуда ;

Отметим, что, приравняв х₃ = - х₁ х₂, можно было получить другую полуреплику 2^3-1. А обе эти полуреплики, взятые вместе, составят ПФП 2³.

Формулы для расчёта коэффициентов регрессии ПФП остаются полностью справедливыми и для ДФП.

Обратимся к построению дробных факторных планов на основе ПФП 2³. Матрица базисных функций этого плана приведена в табл. 12.3.

Таблица 12.3

Матрица базисных функций ПФП 2³

Номер опыта	xо	х1	х2	х3	х1 х2	х1 х3	х2 х3	х1х2 х3	y
1	+1	-1	-1	-1	+1	+1	+1	-1	y1
2	+1	+1	-1	-1	-1	-1	+1	+1	y2
3	+1	-1	+1	-1	-1	+1	-1	+1	y3
4	+1	+1	+1	-1	+1	-1	-1	-1	y4
5	+1	-1	-1	+1	+1	-1	-1	+1	y5
6	+1	+1	-1	+1	-1	+1	-1	-1	y6
7	+1	-1	+1	+1	-1	-1	+1	-1	y7
8	+1	+1	+1	+1	+1	+1	+1	+1	y8

Имеется несколько способов построения полуреплики с четырьмя факторами на основе этого плана в зависимости от того, каким из взаимодействий решено пренебречь. Так, пренебрегая тройным взаимодействием х₁ х₂ х₃ и заменив соответствующий столбец фактором х₄, получим следующий план для четырёх факторов (одна из полуреплик 2^4-1, табл. 12.4).

Для этого плана имеем генератор х₄= х₁х₂х₃. ОК равен 1 = х₁х₂х₃ = х₄. Умножая OK последовательно на х₁, х₂, х₃, х₁х₂, х₁х₃, х₂х₃, получаем новые генераторы: х₁ = х₂х₃ х₄; х₂ = х₁ х₃ х₄; х₃ = х₁ х₂ х₄; х₁ х₂ = х₃ х₄; х₁ х₃ = х₂ х₄; х₂ х₃ = х₁ х₄.

В результате имеем следующую систему смешивания оценок:

Таблица 12.4

ПФП 2^{4– 1} х₄= х₁х₂х₃

Номер опыта	х1	х2	х3	х4	y
1	-1	-1	-1	-1	y1
2	+1	-1	-1	+1	y2
3	-1	+1	-1	+1	y3
4	+1	+1	-1	-1	y4
5	-1	-1	+1	+1	y5
6	+1	-1	+1	-1	y6
7	-1	+1	+1	-1	y7
8	+1	+1	+1	+1	y8

В уравнение регрессии, построенное по результатам реализации такого плана, можно включить, кроме линейных членов, все парные взаимодействия, приведённые в плане табл. 12.3:

(12 .9)

Однако надо помнить о системе смешивания. К примеру, коэффициент b₁₂ оценивает не только при β ₁₂, но и β _34.

План в табл. 12.4, используемый для построения модели (12.9), является насыщенным, число опытов в нём N = 8 равно числу оцениваемых коэффициентов регрессии. Поэтому нет возможности проверить адекватность модели. Такую проверку можно сделать, если упростить уравнение (12.9), пренебрегая в нём дополнительно ещё некоторыми взаимодействиями.

Рассмотрим другой вариант полуреплики, приравняв, например, х₄ парному взаимодействию х₁ х₃. Этот план приведён в табл. 12.5.

ОК такой реплики: 1 = х ₁ х ₃ х ₄ . Генераторы плана: х ₁ = х ₃ х ₄ ;

Таблица 12.5

ДФП 2^4-1 х₄ = х₁х₃

Номер опыта	х1	х2	х3	х4	y
1	-1	-1	-1	+1	y1
2	+1	-1	-1	-1	y2
3	-1	+1	-1	+1	y3
4	+1	+1	-1	-1	y4
5	-1	-1	+1	-1	y5
6	+1	-1	+1	+1	y6
7	-1	+ 1	+1	-1	y7
8	+1	+1	+1	+1	y8

Система смешивания оценок:

Сравнивая системы смешивания оценок для двух последних планов, можно убедиться в преимуществах плана с OK 1 = x₁ х₂х₃ х₄. Для него оценки линейных коэффициентов регрессии смешаны лишь с тройными взаимодействиями, в то время как для плана с OK 1 = x₁ х₃ х₄ некоторые из этих оценок смешаны с парными взаимодействиями. Отсюда следует вывод: с точки зрения системы смешивания оценок, лучше выбирать реплипки, в правой части ОК которых стоит максимальное число членов.

Кроме предложенных вариантов, можно рассмотреть ещё 6 способов построения полуреплик на основе ПФП 2³. Их генераторы:

Идею построения ДФП можно развивать дальше, заменяя в планах ПФП не одно, а большее число взаимодействий новыми факторами. При замене двух взаимодействий новыми факторами получим четверть-реплики (или 1/4 реплики) ПФП. Их условное обозначение 2^{к- 2}.

В табл. 12.6 приведён план 1/4 реплики для 5 факторов, полученный заменой в ПФП 2³ взаимодействий x₁ х₂ х₃ и х₂ х₃ факторами х₄ и х₅ соответственно.

Таблица 12.6

ДФП 2^{5 - 2}

Номер опыта	х1	х2	х3	х4	х5	y
1	-1	-1	-1	-1	+ 1	y1
2	+1	-1	-1	+1	+ 1	y2
3	-1	+1	-1	+1	-1	y3
4	+1	+1	-1	-1	-1	y4
5	-1	-1	+1	+1	-1	y5
6	+1	-1	+1	-1	-1	y6
7	-1	+1	+1	-1	+ 1	y7
8	+1	+1	+1	+1	+ 1	y8

При замене в ПФП трёх взаимодействий новыми факторами получают 1/8 реплики ПФП, обозначаемые 2^к-3 и т. д.

На основе ПФП 2³ можно построить дробную реплику, включающую самое большее 7 варьируемых факторов. Это будет план 2^{7 - 4}, представляющий собой 1/16 реплики от ПФП 2³.

В табл. 12.7 приведён этот план, построенный с помощью следующих генераторов: x₄= x₁x₂; х₅ =x₁x₃ ; х₆ = х₂ х₃; х₇ = x₁x₂ x₃.

С помощью такого плана можно получить линейную модель

(12,10)

однако нельзя проверить адекватность такой модели, так как план 2^7-4 является насыщенным.

Насыщенные дробные факторные планы часто используют в качестве планов отсеивающего эксперимента, основная цель которых не построение адекватной модели, а выявление важнейших переменных из числа варьируемых факторов.

Таблица 12.7

ДФП2^{7 - 4}

Номер опыта	х1	х2	х3	х4	х5	х6	х7	y
1	-1	-1	-1	+1	+1	+1	-1	y1
2	+1	-1	-1	-1	-1	+1	+1	y2
3	-1	+1	-1	-1	+1	-1	+1	y3
4	+1	+ 1	-1	+1	-1	-1	-1	y4
5	-1	-1	+1	+1	-1	-1	+1	y5
6	+1	-1	+1	-1	+1	-1	-1	y6
7	-1	+1	+1	-1	-1	+1	-1	y7
8	+1	+1	+1	+1	+1	+1	+1	y8