2) Дифференцирование степенных рядов.

3) Сложение, вычитание, умножение и деление степенных рядов.

,

 Коэффициенты с_i находятся по формуле:

_, ,

№ 17.

] D € , D-квадрируемая фигура, z=f(x,y) на D. Разбиваем D на части спрямляемыми кривыми.площадь,-диаметр,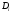

Составление суммы сигма

Выбираем точку =€, су двумерная интегральная сумма F(x,y) на обл. D.

Число J наз. пределом интег. при, если<

Несобственный кратный интеграл

Двойным интегралом ф f(x,y) по мн-ву D называется предел интегральных сумм σ при

Если двойной интеграл -> f(x,y) интегрируема во множестве D.

Геометр-ий смысл:Если z=f(x,y)>0, то

Терема:Интегрируемая Функция ограничена.

Н. и Д. условия интегрируемости ф-ий .

] D € , D-квадрируемая фигура, z=f(x,y) на D. Разбиваем D на части спрямляемыми кривыми.площадь,-диаметр,

- при заданном разбиении Т, тогда

,-нижняя и верхняя суммы Дарбу, отвечающие разбиению.

Свойства:

1.,

2. При добавлении к старым новых линий деления , ниж-я сумма неуменьшается , а верхняя не увеличивается.

3. ниж-я сумма s не превосходит вер-ю сумму S.

4.

Теорема: Критерий -я двойн-го интеграла от огр-ой на D ф-ии f(x,y). Д.т.ч. огр-я на D ф-я f(x,y) была интегрируема Н. и Д. чтобы:

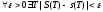
Теорема:Огр-я на D ф-я f(x,y) интегрируема

Теорема: Неп-я ф-я инт-ма на ограниченной области(завмкнутой) D.

Основные св-ва двойных интег-ов.

• Если ф-ии f(x,y) и g(x,y) инт-мы на D, то f+g инт-ма на D и вып-ся:

Док-во:

Т.к. f и g инт-мы на D

• Если ф-ия f(x,y) инт-ма на D и k-некоторое действительное число, то ф-ия k*f инт-ма на D и справедливо рав-во:

• ] D объединение 2-х мн-в и, гдеи-квад-я, не имеющая общих точек фигураf(x,y) инт-ма на D инт-ма наипричем верно:

=

• ] f инт-ма и огр-на на D

• Если f инт-ма на D и f(x,y)0 (f(x,y)0))(x,y) € D

• Если f g инт-мы на D и вып-ся f(x,y)g(x,y) 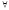(x,y) € D (x,y) € D

• Если ф-я инт-ма на D, то |f| инт-ма на D, причем вып-ся

• Т-ма о среднем Если ф-я f(x,y) в связ-ой квад-ой области D инт-ма, то такая точка €D,

Что

Замена переменных в двой-ом интеграле.

T € UOV, F-регулярное отображение

F(t)=D, f(x,y)- неп-на на D, тогда

Геометрические приложения:

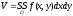-объем цилиндрического тела.

-прямоуг-я сис-а координат

-в сфер-ой сис-е координат

- в поляр-ой сис –ме коор-т

Вычисление массы материальной пластины и материального тела

] D-некоторая мат-я пластина, плоская квадрируемая фигура. (m и p-не зависят от x,y)

D разбив. на n частей, не имеющих общих точек. 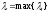,€ D ,-предполагается, что начастичке-плотность постоянна,

- масса математической пластинки.

, p(x,y,z)-непр-на на ,-разбив-ся на n,,

,

-масса мат-го тела.

Крив-ый интеграл 2-го рода и его основные св-ва.] задана нек-я вектор-я функция на дугу ,

, ,

, ,,

Определение: Если конечный предел lim, то он называется криволинейным инт-ом 2-го рода от вектор-функции

Физ-ий смысл: A силы, к-ая совершается при движении точки вдоль дуги AB

Св-ва

1. 

,

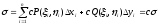2

.

3. Если криволинейный интеграл по дугам AC и СВ не имеющим общих точек , то

3. При изменении направления движения точки интеграл изменяется на противоположный

Формула Грина устанавливает связь между крив-м интегралом по границе некоторой области и двойным инт-ом этой области.

Если D можно разбить на части только 1-го и 2-го вида: D-односвязная область, огран-я кусочно-гладкой кривой L, а P и Q неп-ны вместе со своими частнами произ-ми

Приложение крив-го инт-ла 2-го рода

Использование для вычисления плошади фигуры.

Работа переменной силы:

Крив-ый интеграл 1-го рода. Определение

] ф-я f(x,y) определена на AB-плоскакая кусочно-гладкая кривая. (i=0,..,n=1). Надуге выбираем т..Интег-я сумма F(x,y) по длине дуги

Определение:Если кон-й, то гов-т, чтоF(x,y) инт-ма по длине, этот инт-л называется крив-м инт-ом 1-го рода и обозначается

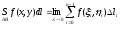
Физ-й смысл: Если AB –мат-я дуга с плотностью p=f(x,y), то S 1-го рода – масса дуги AB

Св-ва

1. ,

2.

3.

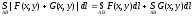
4.

5.

6. ,L-длина дуги

7.

Приложение криа-го инт-ла 1-го рода

1 L=-длина кривой

2. m=-масса кривой, p(x,y)-плотность распределения массы по дуге AB.

3.AB-является нап-ей цил-ой пов-ти,тогда площадь поверности зад-я ф-ей z=f(x,y)

S=

Поверхностные инт-лы 1-го рода.

U=f(x,y.z) задана в . Пов-бтьразбивается на части. Площадь каждой частички,

-диаметр, . На элемен-ой пов-ти выб-ся точкаи считывается значение в этой точке-инт-я сумма от ф-и U по пов-ти.Если кон-й предел этой суммы, то он называется пов-м инт-м 1-го рода и обознач-ся:

Т-ма о неп-го инт-ла:Если F(x,y.z) неп-на, а пов-ть считается гладкой вточкекасс-я пл-ть, к-я непрерывно меняется с перемещением точек по пов-ти, тогда пов-ый инт-л 1-го рода.

Св-ва:

1.

,граница

, 2.

3.

4.

5. ,

6.

7.

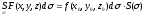
Приложение пов-го S 1-го рода

Масса поверхности-m=,-плотность

Стат-е моменты

Поверхностный интеграл 2-го рода

Поверхность наз-тдвусторонней , если обход по замкнутой линии, лежащей на этой пов-ти и не имеющей общих точек с границей этой пов-ти не меняет направление ее нормали.

Двууст-ие пов-ти Z=Z(x,Y),x=x(y,z),y=(x,z)

Если выбир-м напрвление нормали, чтобы < был острый с соответ-ей осью, то будем обходить вернюю сторону пов-ти.

зам-я пов-ть не имеющ-я точек самопересечения яв-ся двусторонней пов-ю.

Определение:

Расс-м нек-ю ф-ию U=f(x,y,z)-задана и неп-на на гладкой ориентир-ой пов – ти . Разбиваем пов-ть наn частей, ввыбираем точку, считаем знач-е ф-ии в этой точке, умноженное на - площадь частички.(-берется с+ если выбрана верхняя сторона пов=ти)

Получим пов-ый инт-л 2-го рода

,, ,

, ,,

Общий вид

Св-ва

1. меняется знак при изменении стороны поверхности.

2. константа выносится за знак интеграла

3. пов-ый инт-л от суммы =сумме соответ-х слагаемых

4. инт-л по всей пов-ти = сумме инт-ов по ее частям , пересекающейся лишь на границе их разделяющей.

5. если - цилиндрические пов-ти, у кот-х образующие // уоси OX,-OY,-OZ

вып-ся рав-ва ,,

Формула Остроградского-Гаусса отражает связь между пов-ми инт-ми 2-города по замкнутой поверхности и тройным интегралом по объему , огран-го этой пов-ю

Теорема:

]ии- неп-ны вместе со своими частными производными 1-го порядка в нек-ой пространственной области Vсправедлива формула

Формула Стокса устан-т связь между пов-ми крив-ми интеграми 2-го рода

Теорема: Ф-ии P,Q,R неп-ны со своими частными производными 1-го пор-ка, в точках ориентированной пов-ти тогда имеет место фориула

Приложение инт-ла 2-го рода

Вычисление объема тела

,

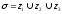
Пусть P=x, Q=0, R=0

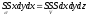
P=0, Q=y, R=0

P=0, Q=0, R=z