4. Интегрирование некоторых тригонометрических функций.

  Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

 Интеграл вида . Здесь R – обозначение рац ф-ции от переменных sinx и cosx.

Подстановка . позволяет преобразовать триг ф в рациональную.

, 

Тогда 

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой

5. Интегрирование некоторых иррациональных функций

Интеграл вида гдеn- натуральное число.

 

С помощью подстановки функция рационализируется.

Тогда

6. Интеграл вида если функцияR является нечетной относительно cosx.

Несмотря на возможность вычисления такого интеграла с помощью универсальной триг подстановки, рациональнее применить подстановку t = sinx.

 

Функция может содержатьcosx только в четных степенях, т.е., может быть преобразована в рациональную функцию относительно sinx.

7. Интеграл вида если функцияR является нечетной относительно sinx.

 По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

Интегрирование элементарных функций

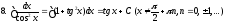
11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл

   Задача. Вычисление площади криволин. трап. Решение. ] y=f(x) опред. на [a,b]. [a,b] разобьем на n частей. a=x₀<x₁<x₂<…<x_n=b. Получим мн-во отрезков [x_i,x_i+1], i=0,..,n, c_i[x_i,x_i+1]=> площ. к-л прямоугольника s_i=f(c_i)Δx_i=f(ci)(x_i+1- x_i) => S_тр приmax Δx_i→0. Чем больше n, тем больше точность: S=

Понятие опред. инт-ла. y=f(x) опред. на [a,b]. [a,b] разобьем на n частей. a=x₀<x₁<x₂<…<x_n=b. И совокуп-ть всех этих тт назовем разбиением [a,b], т.е. T={x_i,i=0,…,n} Δ_i =[x_i,x_i+1] i=0,…,n-1, Δx_i =x_i-1 - x_i. Мелкость разбиения l=max Δx_i, i=0,…,n-1. c_i Δ_i, i=0,…,n-1. Совокуп-ть тт c_i назовем выборкой C. C={c_i, i=0,…,n-1}. Составим след. сумму: - интегральная сумма. ЧислоI наз. опред. инт-м ф-и y=f(x), зад. на [a,b], если

x_i+1

Будем считать,что ф-я y=f(x), зад. на [a,b] и огр. на нем, т.е. сущ-т m, M: mf(x) M. ] - нижняя интегр. сумма Дарбу.- верхняя интегр. сумма Дарбу.Св-ва сумм Дарбу.

1.;

2. При заданном разбиении отрезка T суммы Дарбу s_T и S_T явл. соотв-но точной нижней и точной верхней гранями интр. сумм, т.е.

3. Разбиение T₂ явл-ся продолжением разбиения T₁, если кажд. точка разбиения T₁ явл. точкой разбиения T₂. Если T₂ - продолжение разбиения T₁, то:

4. Для любых разбиений Т′, Т′′ , т.е. нижняя сумма никогда не превзойдет верхней для любого разбиения.

Из св-ва 4 след., что мн-во нижних сумм огр-но сверху => сущ-т точная верхняя грань .наз. интегралами Дарбу.

Условие сущ-я опред. интеграла. Для сущ-я опред. инт-ла н. и д., чтобы .

Д-во.

Необх-ть. ] сущ-т опр. инт.

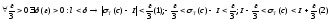
. Сложим 2 послед. нер-ва:

Дост-ть. ; ;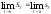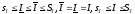. Докажем, чтоI – именно интеграл. Т.к.

Из чертежа:

. ЧТД.

Свойства определённого интеграла.

1..

2..

3. Пусть функции f(x) и g(x) интегрируемы на, то их сумма также интегрируема на этом отрезке и интеграл от суммы равен сумме интегралов.

4. Если f(x)>=0 (f(x)<=0) на [a,b], то

5. Если на отрезке [a,b]a<b, функцииf(x) иg(x) удовлетворяют условию f(x) >= g(x), то.

Д-во. Введём в рассм-е ф.φ(x)=f(x)-g(x)>=0 =>

6. для любых точек a, b и c a<c<b .

7. если M и m – наибольшее и наименьшее значения функции f(x) на отрезке [a,b], то .Д-во.

8. теорема о среднем: если функция f(x) на отрезке [a,b] непрерывна, то на этом отрезке найдется такая точка, что справедливо:

доказательство:

пусть для определенности a<b. Еcли m,M суть соответственно наибольшее и наименьшее значения f(x) на отрезке [a,b], то в силу 7. имеем:

так как f(x) непрерывна , то она принимает все промежуточные значения междуm,M. следовательно при некотором значении. ЧТД.

. Покажем, что неопред. интегр. есть опред. с перемен. верхним пределом: Придадим x приращение Δx.

(по теор. о сред.). Разделим рав-во на Δx:. По теор. о 2х милиционерах;. Т.о.,I(x) явл-ся первообразной f(x): . ]x=a => 0=F(a)+C => C= -F(a). . ]x=b => - ф-ла Ньютона-Лейбница.

Замена переменной в определенном интеграле.

Тh. Пусть дан иx=φ(t) на [α,β], причем φ(α)=a, φ(β)=b, область зн-й ф-и не выходит за пределы [a,b]. φ(t) непр-на, имеет φ′(t) => имеет место ф-ла: .Д-во. .

Интегрирование по частям. ] u,v – диф-е ф-и от x. . Интегрируя обе части в части в [a,b], получим . Т.к.. Поэтому или .

Применение оп. инт. к вычислению геом., механич. и физических величин. 1) Площадь криволинейной трапеции 2) Вычисление длины дуги кривойи если кривая задана параметрически:3) Вычисление объёма тела по площ. параллельн. сечений:, гдеQ(x) – ур-е площади попереч. сечения