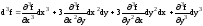- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
12. Функции нескольких действительных переменных.
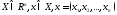 ,
,
 - ф-я
- ф-я -переменных
(
-переменных
( - действительно).
- действительно).
Графиком
является
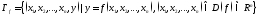 .
.
Для ф-ций нескольких переменных справедливы определения предела, непрерывности и теоремы о непрерывных функциях так же, как для функций одного переменного.
Опр.
Для функции z=f(x,y)

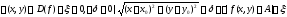
Непрерывность
функции. Опр.
Пусть
![]() - некоторая точка, и функция
- некоторая точка, и функция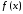 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки![]() .
Назовём функцию
.
Назовём функцию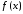 непрерывной
в точке
непрерывной
в точке
![]() ,
если существует предел функции при
,
если существует предел функции при![]() ,
и этот предел равен значению функции
в точке
,
и этот предел равен значению функции
в точке![]() :
: .
.
Терема
Больцано-Коши 1. Если
ф-я
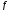 опр-на и непр-на на отрезке
опр-на и непр-на на отрезке и на концах отрезка принимает значения
разных знаков, то м/у точками
и на концах отрезка принимает значения
разных знаков, то м/у точками и
и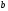
 ,
такая, что
,
такая, что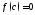 .
.
Док-во:
Делим
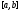 пополам. Выбираем тот отрезок, в левом
конце которого ф-я принимает отриц.
значение, а в правом – положительное,
обозначим
пополам. Выбираем тот отрезок, в левом
конце которого ф-я принимает отриц.
значение, а в правом – положительное,
обозначим .
Если оказалось, что в точке деления ф-я
равна нулю, то ч.т.д.
.
Если оказалось, что в точке деления ф-я
равна нулю, то ч.т.д.
Делим
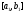 пополам. Если в точке деления ф-я равна
нулю, то ч.т.д. Если нет, то делаем
описанную выше процедуру.
пополам. Если в точке деления ф-я равна
нулю, то ч.т.д. Если нет, то делаем
описанную выше процедуру.
В
итоге получим посл-ть вложенных отрезков:
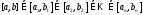 .
.


По
принципу вложенных отрезков
 .
.
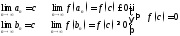 ч.т.д.
ч.т.д.
Терема Больцана-Коши 2. Пусть f(x) опр. и непр на отр [a,b], и на концах этого отр принимает неравные зн-я f(a)=A, f(b)=B, A≠B, тогда для любого числа С, A<C<B, найдется такое число с, a<с<b, что f(c)=C.
Равномерная
непрерывность функций. Пусть
![]() - некоторая функция и
- некоторая функция и![]() .
Функция
.
Функция![]() равномерно
непрерывна
на
равномерно
непрерывна
на
![]() ,
если
,
если![]()
Из равномерной непрерывности следует непрерывность, обратное не верно.
Компакты
в метрических пространствах.
 - метрическое
пространство
- метрическое
пространство
 .
МножествоM
называется компактным, если любая
подпоследовательность его точек
содержит сходящуюся подпоследовательность,
предел которой
.
МножествоM
называется компактным, если любая
подпоследовательность его точек
содержит сходящуюся подпоследовательность,
предел которой
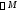 .МножествоM
открыто, если все его точки внутренние.
Замкнуто, если оно одержит все свои
предельные точки.
.МножествоM
открыто, если все его точки внутренние.
Замкнуто, если оно одержит все свои
предельные точки.
Т.1 Если мн-во компактно, то оно ограничено. Т2. Если мн-во компактно, то оно замкнуто.
Мн-во в метрич.пр-ве наз-ся ограниченным, если оно содержится в некотором шаре.
Обобщение
теорем Вейерштрасса:
Если
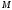 - компакт в МП, а
- компакт в МП, а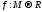 непрерывна, то множество значений этой
ф-ции огр. и среди них есть наим. и наиб.
значение.
непрерывна, то множество значений этой
ф-ции огр. и среди них есть наим. и наиб.
значение.
Док-во:
Т.к. образ
компакта при непрерывном отображении
есть компакт,
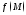 - ограничен и замкнут, и
- ограничен и замкнут, и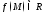 ,
то и в
,
то и в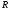 ограничен и замкнут и достигает своих
наиб. и наим. значений. ч.т.д.
ограничен и замкнут и достигает своих
наиб. и наим. значений. ч.т.д.
Теорема
Больцано-Вейерштрасса. В
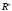 из
любой ограниченной последовательности
можно извлечь сходящуюся
подпоследовательнсоть.
из
любой ограниченной последовательности
можно извлечь сходящуюся
подпоследовательнсоть.
Обобщение теоремы Кантора. Непрерывное отображение компакта равномерно непрерывно.
Метрическое
про-во. Метрикой(расстоянием) на множестве
E
называется функция
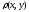 ,
удовл. усл-м:
,
удовл. усл-м:
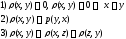
Мн-во E с заданной на нем метрикой называется метрическим пространством (E,p)
13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
Задана
прямая в метрич. пространстве:
 .Производная
функции f в точке x0
по направлению
e наз. следующий предел:
.Производная
функции f в точке x0
по направлению
e наз. следующий предел:
 .
Если в кач-ве направления исп-ся
координатные орты, то такие производные
наз.частными
производными ф-ции
f.
.
Если в кач-ве направления исп-ся
координатные орты, то такие производные
наз.частными
производными ф-ции
f.
Замеч. Механич. смысл производной по направлению – скорость изменения ф-ции в данном направлении.
Теорема. При замене направления на противоположное производная по направлению меняет только свой знак.
Д-во.
Пусть даны e1,
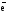 ,
e2,
-
,
e2,
-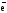 .
.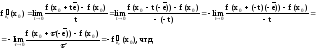
Пусть задана ф-ция трех перем-х u=f(x,y,z). Берется точка (x0, y0, z0). Будем искать производную по x.
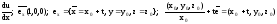 .
.
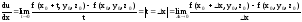 .
.
Точка
(x0,
y0,
z0)
вдоль вектора
 :
: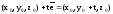
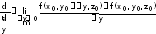 .
.
Точка
(x0,
y0,
z0)
вдоль вектора
 :
: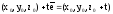 ;
;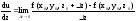 .
.
Правило для нахождения частных производных: частная произв-я по x находится как произв-я ф-ции одной переменной x при условии, что остальные перем-е фиксированные.При этом справедливы все правила для вычисления производных.
Замеч. Ф-ция, иеющая в данной т. частные произв-е или даже равные произв-е по всем направлениям, может не быть непрерывной в некот. т.
Дифференцируемость ф-ции в точке.
Ф-ция,
кот-я отображает простр-во L:
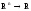 ,
и определ-ся равенством
,
и определ-ся равенством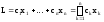 наз.
линейным функционалом.
наз.
линейным функционалом.

Св-ва
линейного функционала:
1)
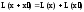 ;
2)
;
2)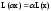 ;
3)
;
3)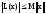 ;
4) Ф-ция L явл-ся равномерно непрерывной.
;
4) Ф-ция L явл-ся равномерно непрерывной.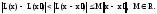
Пусть
ф-ция f:
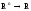 и
и
 ,
x0 –
внутр-я т. мн-ва D. Ф-ция f наз. дифференцируемой
в т. x0,
если в окрестности т. x0
ее приращение можно представить в виде:
,
x0 –
внутр-я т. мн-ва D. Ф-ция f наз. дифференцируемой
в т. x0,
если в окрестности т. x0
ее приращение можно представить в виде:
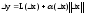 .
(1)
.
(1)
x=(x1,…,xn);
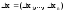 ;
;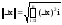
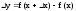 ;
;
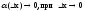 .
.
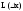 -
наз. дифференциалом
ф-ции f в т.
x0.
-
наз. дифференциалом
ф-ции f в т.
x0.
 (2)
(2)
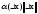 -
бесконечно малое более высокого порядка,
чем
-
бесконечно малое более высокого порядка,
чем
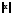 ,
поэтому
,
поэтому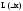 есть главная линейная часть приращения.
Следовательно формула для получения
приближенного вычисления:
есть главная линейная часть приращения.
Следовательно формула для получения
приближенного вычисления: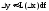 .
.
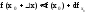
Св-ва диф-мых ф-ций:
Пусть f и g диф-мы в некоторой т. x0 и a – некоторое действительное число, тогда d(f+g)=df+dg, d(af)=adf.
Теорема. Если ф-ция диф-ма в данной т., то она в ней непрерывна.
Док-во:
ф-ция
 диф-ма в т.
диф-ма в т.
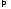 ее приращение имеет вид
ее приращение имеет вид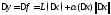 .
.

 непр.
в т.
непр.
в т.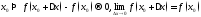 .
Обратное не верно, ч.т.д.
.
Обратное не верно, ч.т.д.
Градиент.
Градиентом
ф-ции в данной т. наз. вектор, координаты
которого являются частными производными
в этой т., обознач-ся:
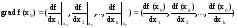 .
.
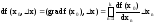 -
частная производная через градиент.
-
частная производная через градиент.
 производная
по направлению через градиент.
производная
по направлению через градиент.
Физический смысл градиента. В направлении градиента ф-ция имеет наибольшую скорость изменения.
Связь дифференцируемости с существованием частных производных.
Теорема(достат. условие диф-ти). Если в каждой т. некоторой окрестности u0 ф-ция W=f(x,y,z) имеет частные производные непрерывные в самой т. u0, то ф-ция диф-ма в т. x0.
Диффер-емость сложных ф-ций и инвариантность формы диф-ла первого порядка.
h(x)=g(f(x));
h(x)=g(u);
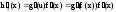 .
.
y=h(x);
 ;
;
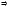
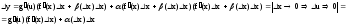
y=f(x1,…,xn) (1)
x=(x1,…,xn),
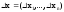
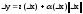 (2)
(2)
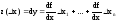
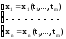 (3)
(3)
 (4)
(4)

Теорема. Пусть ф-ции (3) диф-мы в некот. точке M0=(t10,…,tm0), а ф-ция y1 диф-ма в точке N0=(x10,…,xn0).
xi0=xi(t10,…,tm0),
тогда сложная ф-ция (1) с равенством (3)
диф-ма в точке M0,
причем справедливо равенство (4), где
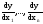 - выч-ся в точке N0,
а
- выч-ся в точке N0,
а
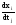 (i=1,…,n; j=1,…,m) выч-ся в точке M0.
(i=1,…,n; j=1,…,m) выч-ся в точке M0.
y=f(x1,x2,x3); x1=x1(t1,t2); x2=x2(t1,t2); x3=x3(t1,t2).
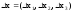 в
точке N0;
в
точке N0;
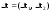 в точке M0.
в точке M0.
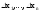 соотв-ет
приращению
соотв-ет
приращению
 ,
т.е. они дают приращение в т. М0
для ф-ции y. Т.к. ф-ция диф-ма, то
,
т.е. они дают приращение в т. М0
для ф-ции y. Т.к. ф-ция диф-ма, то
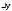 имеет вид:
имеет вид: (5).
Т.к. ф-ции (3) – диф-мы, то:
(5).
Т.к. ф-ции (3) – диф-мы, то: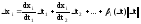 ,
i=1,2,…,m(6).
,
i=1,2,…,m(6).
Подставим
рав-во (6) в рав-во (5) и сгруппируем
относительно
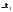 и
и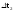 .
.
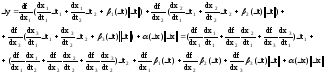

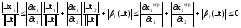
 ;
;
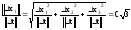
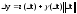 ;
;
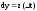
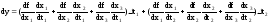 (7)
(7)
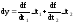 (8)
(8)
Из
формул (7) и (8) получаем:
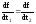 ,
чтд.
,
чтд.
Частные производные.
f: MRnR
y=f(x1,…,xn)
Пусть
в М0М.
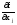 (j=1,…,n).
(j=1,…,n).
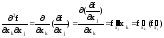
При kj наз. смешанной производной второго порядка.
При
k=j обознач.
 - частн. произв. второго порядка.
- частн. произв. второго порядка.
Если окажется, что и они диф-мы по переменным x1,…,xn, то то аналогично определяются производные третьего порядка. Если и они окаж-ся диф-мы, процесс можно продолжить, то получается частная произв-я или частная смешанная произв-я m-порядка.
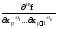 ,
,

Теорема. (Достаточное условие рав-ва смешанных производных)
z=f(x,y)
fxy , fyx - две смешанных частн. произв-х.
Если две смешан-е частные произв-е fxy , fyx в окр-ти точки (x0, y0) и непр. в этой точке, то они в этой точке совпадают: fxy(x0,y0)=fyx(x0,y0).
Диф-лы высших порядков.
f: MRnR
y=f(x1,…,xn)
Ф-ция
f диф-ма внутри М
df(x, ).
).
x=(x1,…,xn),

Фиксируем
 ,
тогда df зависит только от x. Если эта
ф-ция имеет диф-л, то он при том же
,
тогда df зависит только от x. Если эта
ф-ция имеет диф-л, то он при том же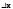 наз-ся вторым диф-лом или диф-лом второго
порядка:
наз-ся вторым диф-лом или диф-лом второго
порядка: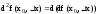 .
Если он оказ-ся диф-мой ф-цией при
фиксированном
.
Если он оказ-ся диф-мой ф-цией при
фиксированном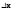 ,
то опред-ся диф-ал третьего порядка, и
так далее. В общем случае диф-ал m порядка
– это диф-ал от диф-ла (m-1) порядка:
dmf(x0,
,
то опред-ся диф-ал третьего порядка, и
так далее. В общем случае диф-ал m порядка
– это диф-ал от диф-ла (m-1) порядка:
dmf(x0,
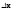 )=d(dm-1f(x0,
)=d(dm-1f(x0,
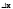 )).
)).
Из
существования диф-лов первого порядка
существование частных производных и
равенство:
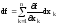 .
.
Из
-ния
диф-лов второго порядка
$-ние
смешанных и частных произв-х второго
порядка, рав-ва смешанных произв-х:
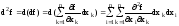
Из $-ния двух частных и смеш-х произв-х и их непр-ти -ние диф-ла второго порядка.
Опр.
Ф-ция B:RnR
и опред-ся равенством
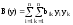 ; y=(y1,…,yn),
bik=bki
– наз. квадратичной формой относительно
y с коэф-ми bik.
; y=(y1,…,yn),
bik=bki
– наз. квадратичной формой относительно
y с коэф-ми bik.
Если
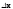 фиксировано и смеш-е частные произв-е
совпадают, то диф-ал второго порядка
оказ-ся квадратичной формой
фиксировано и смеш-е частные произв-е
совпадают, то диф-ал второго порядка
оказ-ся квадратичной формой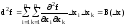
Диф-ал
m порядка – это m-ичная форма относит-но
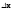 .
.
z=f(x,y)
Если
смешан-е произв-е совпадают, то диф-ал
имеет вид